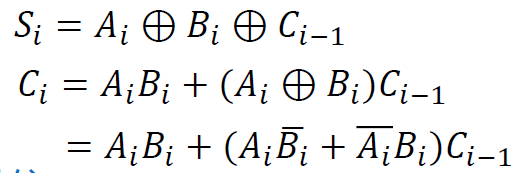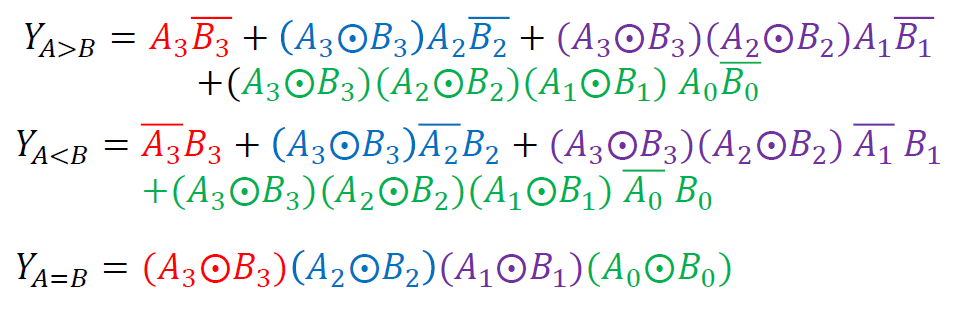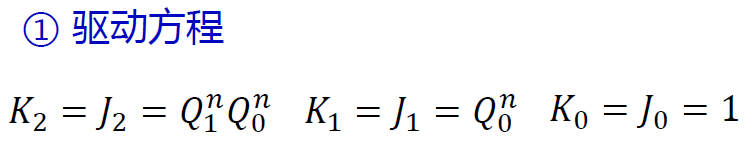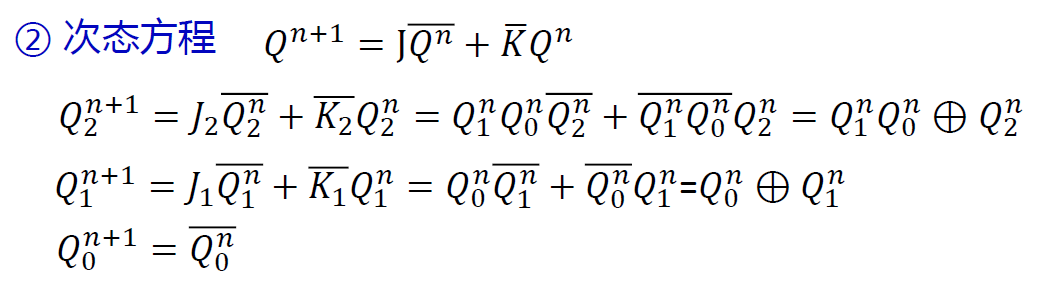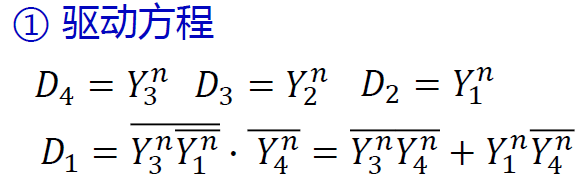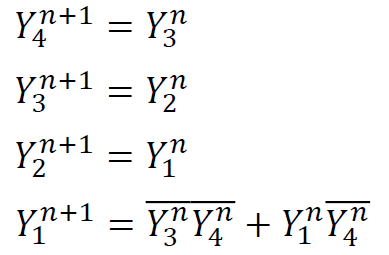数字电路与逻辑设计
第 ○ 章 数字系统介绍¶
1.简介¶
-
数字系统: 一个能对数字信号 进行加工、传递和存储的实体,它由实现各种功能的数字逻辑电路相互连接而成
- 例如, 数字计算机就是一种最具代表性的数字系统。
-
模拟信号与数字信号
-
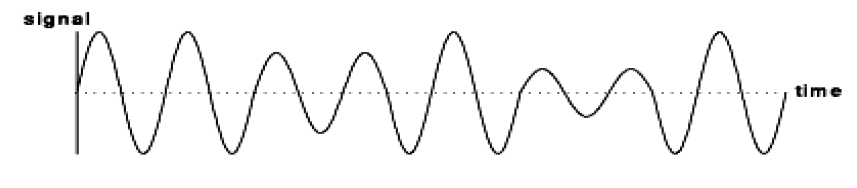
模拟信号: 数值的变化在时间上是连续的
-
数字信号 : 数值的变化在时间上是不连续的
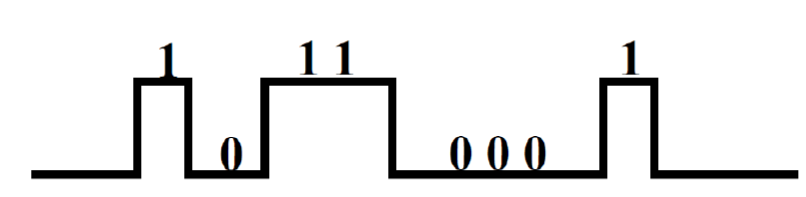
-
-
模拟电路与数字电路
- 模拟电路处理模拟信号 (滤波 放大 时钟 振荡)
- 数字电路处理数字信号
2. 数字电路¶
-
数字逻辑
- 1854 年 ,乔治 布尔( George.Boole )提出逻辑代数(布尔代数(Boolean))
- 1938 年 ,香农注意到电话交换电路与逻辑代数之间的类似性,把逻辑代数的“真”与“假”和电路系统的“开”与“关”对应起来,并用 1 和 0 表示;
-
数字逻辑电路的分类
-
数字集成电路 是数字系统功能实现的基础,基本逻辑单位 是逻辑门电路。
- 逻辑门是数字逻辑电路中能完成独立逻辑功能的一组电子元件和器件所组成的线路基本单元。
<img src="数字电路与逻辑设计.assets\image-20221127163437638.png" alt="image-20221127163437638" style="zoom:50%;" /> -
按电路组成的结构来分 : 分立元件电路和集成电路
- 分立元件电路:将元件和器件用导线连接起来的电路; - 集成电路:将元件. 器件和导线均用半导体工艺集成制作在同一块硅片上构成的电路。
-
按集成度的大小来分
- 集成度大小是指同一块集成芯片上制作的逻辑门电路和元器件数量的多少。集成的逻辑门数量越多,集成度越高,芯片所能实现的逻辑功能就越强 -
 - 1965 年,英特尔联合创始人戈登 · 摩尔提出以自己名字命名的「摩尔定律」,意指集成电路上可容纳的元器件的数量每隔 18 至 24 个月就会增加一倍,性能也将提升一倍。
- 1965 年,英特尔联合创始人戈登 · 摩尔提出以自己名字命名的「摩尔定律」,意指集成电路上可容纳的元器件的数量每隔 18 至 24 个月就会增加一倍,性能也将提升一倍。 -
按电路有无记忆功能来分 : 组合逻辑电路和时序逻辑电路
- 组合逻辑电路——无记忆功能 - 时序逻辑电路——有记忆功能
-
-
与模拟电路相比,数字电路使用二进制的优点:
- 电路简单;
- 对电器元件要求不高;
- 可靠稳定;
- 精确;
- 存储;
- 计算机处理;
第一章 基本知识¶
1. 数制及其转换¶
-
十进制转二进制
- 整数: 余数短除法
- 小数: 乘法取整运算 (保留到小数点后五位, 使用 0 舍 1 入法)
-
二进制转八进制 / 十六进制
- 八进制每三位分割, 十六进制每四位分割, 整数部分向前补 0, 小数部分向后补 0, 转化为对应数制
- 十六进制用()H / ()h表示
2. 原反补码¶
- 原码: 符号位+数字 (0 正, 1 负)
- 反码: 正数不变;负数在原码基础上, 将数字部分按位取反
-
补码: 正数不变;负数在反码基础上+1(最低位+1)
- 快速获得补码: |X|从右边数第一个 1 及其右边保持不变,左边按位取反。(符号位也取反)
- 获得负数的补码: 从右边数第一个 1 及其右边保持不变,左边按位取反
-
小数的原反补也一样
3. 几种常用的编码¶
3.1 BCD 码¶
- BCD(Binary Coded Decimal)码: 用==四位== 二进制数表示==一位== 十进制数码(0~9)
- 分为有权码(8421 码 2421 码)和 无权码 (余 3 码)
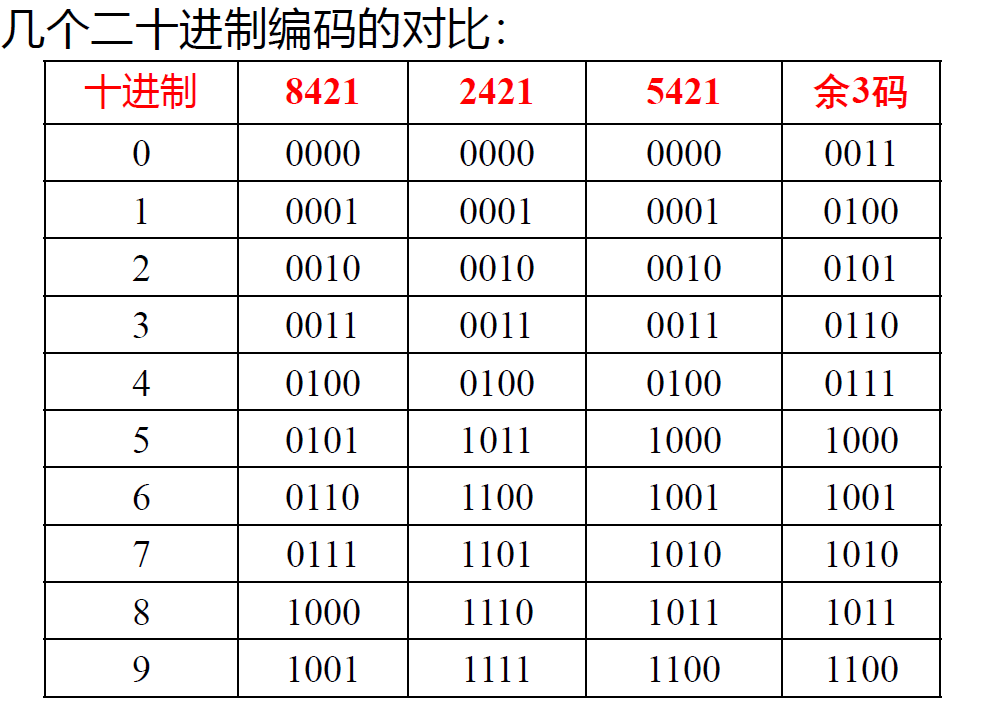
- 8421 码: 四位二进制码的权分别为 23, 22, 21, 20
- 8421 的加法修正规则较为复杂
- 6 组冗余码为 (1010~1111]
- 2421 码: 四位二进制码的权分别为 2, 4, 2, 1
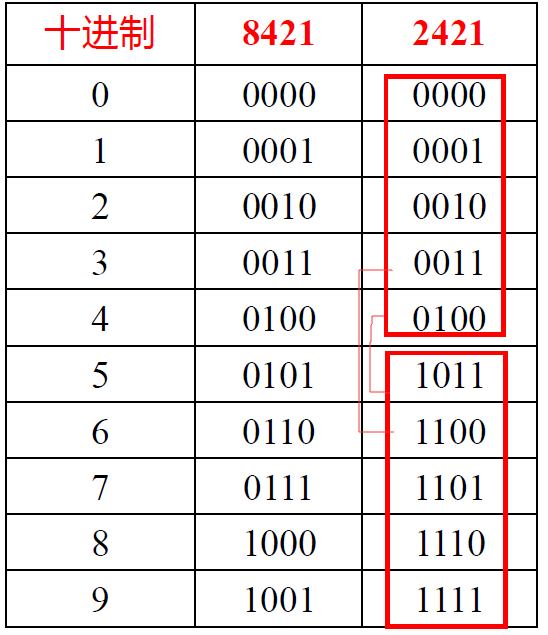
- 对9自补
- 冗余码位于中间 [0101, 1010] (中间空6个)
- 余 3 码: 在==8421 码基础== 上加上 0011(即 3) 形成的无权码
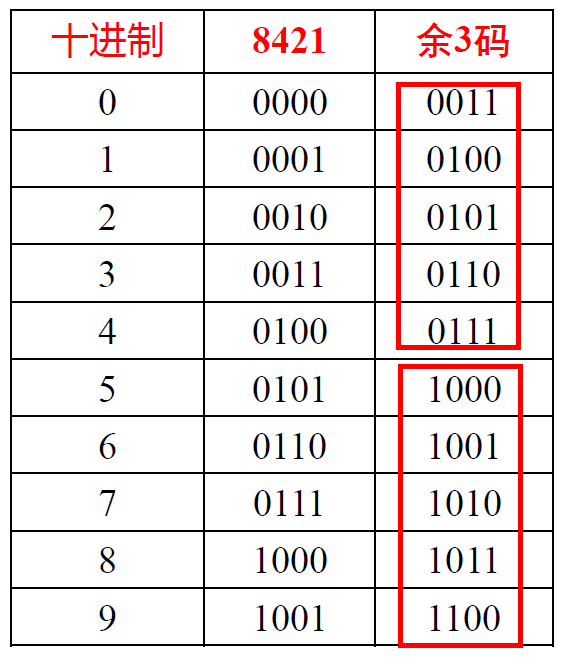
- 同样对9自补
- 冗余码位于两端, [0000~0011), (1101~1111] (两端各空3个)
-
将一个数转化为余三码
- 转化为十进制数
- 转化为 8421BCD 码
- 转化为余三码
-
余 3 码的==加法== : 如果有进位, 则结果+3, 如果没有进位, 结果-3
- 解释:
- 余三码要保证结果正确, 其每一位都应该是 8421 码+3 * -3: 两个加数在转化为余三码的过程中, 每一位上都加过 0011, 总和+6 , 结果需要-3, 才能变为+3 的余三码
- +3: 进位之后, 由 16 进制转为了 10 进制, 相当于==-6== , 结果总和为(+6-6=0)需要+3 成为余三码
3.2 可靠性编码¶
-
纠错的三个层次
- 编码本身不易出错: 格雷码
- 出错能够检查出来: 奇偶检验码
- 检查并能够自我纠错: 海明码
-
格雷码(Gray Code)
- 格雷码: 任意相邻的代码只有一位二进制数不同
-
目的: 在数字变化时, 减少位数的变化次数, 以减少错误的发生
-
编码规则: 由==自然二进制码== (注意: 并非 BCD 码)转换得来
- 设二进制数为 B=Bn-1Bn-2...Bi+1Bi...B1B0, 对应的格雷码为 G=Gn-1Gn-2...Gi+1Gi...G1G0
则有: ①G~n-1~=B~n-1~<font color='orange'>(首位相同)</font> ②G~i~ = B~i+1~ $\oplus$ B~i~ <font color='orange'>(异或)</font>- 生成格雷码步骤
1. 格雷码复制最高位 2. 格雷码之后的每一位与原码的前一位进行异或运算
-
奇偶检验码
-
组成: 信息位 + 校验位(1 位) = 奇/偶校验码
-
分类:
- 奇校验: 使信息位+校验位中 1 的个数为奇数 (凑成奇数) - 奇校验位(以 8421 码为例): \(𝑃=𝐵_8\oplus 𝐵_4 \oplus 𝐵_2\oplus 𝐵_1 \textcolor{#ee0000}{\oplus1} = \overline{𝐵_8\oplus 𝐵_4 \oplus 𝐵_2\oplus 𝐵_1}\) - 偶校验: 使信息位+校验位中 1 的个数为偶数 (凑成偶数) - 偶校验位(以 8421 码为例):\(𝑃=𝐵_8\oplus 𝐵_4 \oplus 𝐵_2\oplus 𝐵_1\)
-
使用例:
- | 被校验信息 | 奇校验码 | 偶校验码 | | ------------------------------------------------ | -------- | -------- | | 10 10 10 10 (4 个 1) | 1 | 0 | | 11 00 11 01 (5 个 1) | 0 | 1 | | 11 01 00 11 (5 个 1) | 0 | 1 | | 10 01 10 01 (4 个 1) | 1 | 0 | | 10 10 11 00 (4 个 1) | 1 | 0 | | 11 10 11 00 (5 个 1) | 0 | 1 |
-
奇偶校验码的检错: 只能检出发生奇数个错误, 并不能纠错
- 例: 使用奇校验传送 1001, 校验位 P=1, 奇校验码为 10011
① 正确传输: $𝑃′=𝐵8\oplus 𝐵4\oplus 𝐵2\oplus 𝐵1\oplus 𝑃=1\oplus 0 \oplus 0 \oplus 1 \oplus 1=1$ **= P** ② 错一位(10<font color='#EE0000'>1</font>11), 检测出错误: $𝑃′=𝐵8 \oplus𝐵4\oplus𝐵2\oplus𝐵1\oplus𝑃=1\oplus 0 \oplus1 \oplus 1 \oplus 1=0 != P$ ③ 错两位(1<font color='#EE0000'>11</font>11), 此时依然奇数个 1, 无法检测出错误
-
第二章 逻辑代数基础¶
2.1 逻辑代数基本概念¶
2.1.1 逻辑变量及基本逻辑运算¶
- 与运算(AND) \(F=A \cdot B\) 或者 \(F=A \land B\)
- 也称为逻辑乘
- 逻辑符号 :
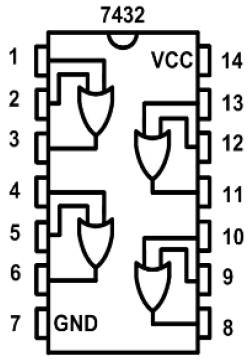
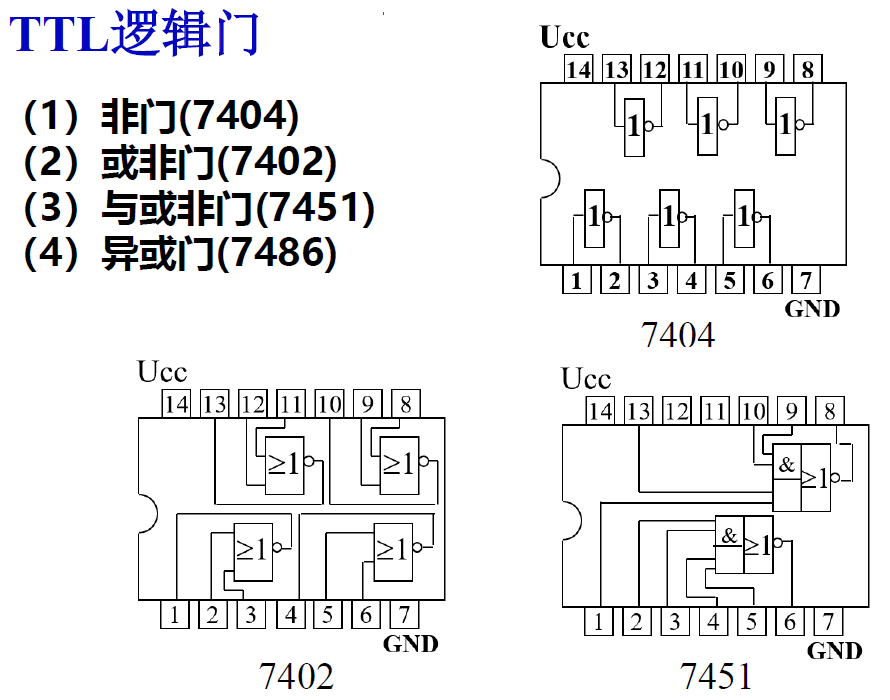
- 典型芯片:74LS08
- 内含 4 个与门, 有 8 个输入, 4 个输出
- VCC 接高电平,GND 接地
- 缺口置于左侧
- 使用:
- 单端 A 输入:① 将 B 置为高电平(\(A\cdot 1 = A\)) 或者 ② 将 B 也置为 A(\(A\cdot A = A\))
- 通过将 1 端置为 0/1, 可以将与门当作开关使用
- 或运算(OR) \(F= A + B\) 或者 \(F=A\lor B\)
- 称为逻辑加
- 逻辑符号
- 典型芯片:74LS32
- 使用:
- 单端 A 输入:① 将 B 置为接地(\(A+0=A\))② 将 B 置为 A(\(A+A=A\))
- 否运算(NOT)\(F = \overline A\) 或 \(F=A'\)
- 也称为反相器
- 逻辑符号:
- 典型芯片: 74LS04
- 逻辑函数
- 定义: 设某一逻辑电路的输入逻辑变量为 A1,A2,…,An,输出逻辑变量为 F,如果当 A1,A2,…An 的值确定后,F 的值就唯一地被确定下来,则 F 被称为 A1,A2,…,An 的逻辑函数,记为 F=f(A1,A2,…,An)。
- 特点 1. 取值: 逻辑 0 / 逻辑 1 2. 运算: 非 > 与 > 或
2.1.2 复合逻辑运算¶
-
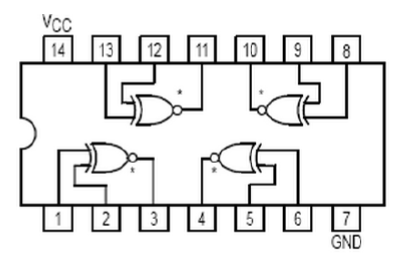
与非(NAND) \(F = \overline{AB}\)
- 逻辑符号
-
典型芯片:
- 7400 二输入与非
- 7420 四输入与非
- 7400 二输入与非
- 逻辑符号
-
或非(NOR) \(F = \overline{A + B}\)
- 逻辑符号
- 典型芯片: 7402
- 逻辑符号
-
与或非(AND-OR-NOT) \(F = \overline{AB+BC}\)
- 逻辑符号:
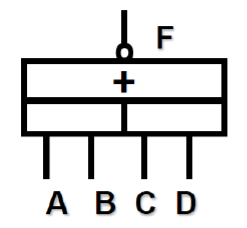
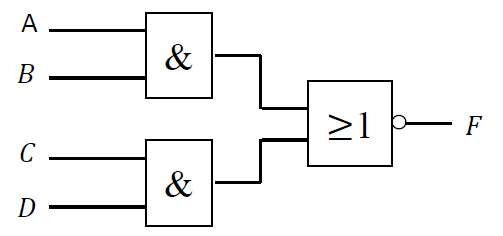
- 典型芯片: 74LS51 ,74LS55
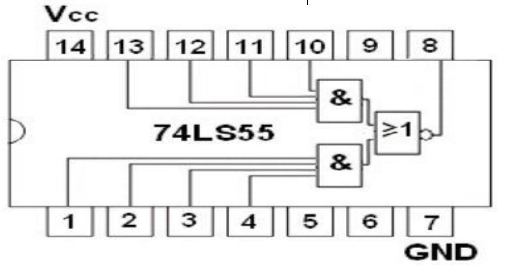
- 故障率高, 不常用
- 逻辑符号:
-
异或 \(F=A\oplus B=\overline {A}B + A\overline{B}\)
- 逻辑符号 :
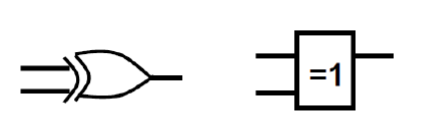
- 真值表 :
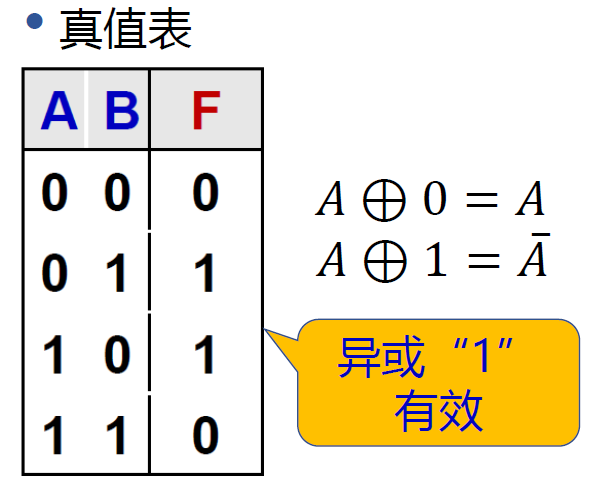
- \(A\oplus 0 = A\), \(A\oplus 1 = \overline A, A\oplus A = 0\)
- 异或计算中的 0 不会对结果产生影响
- -> 奇数个 1, 结果为 1;偶数个 1,结果为 0
- 典型芯片:74LS86
- 用途
- 加法的半加器
- 原码/反码输出
- 等同比较
- 奇偶校验
- 逻辑符号 :
-
同或 : \(F = A\odot B = \overline{A}\ \overline{B} + AB\)
- 逻辑符号:
- 真值表:
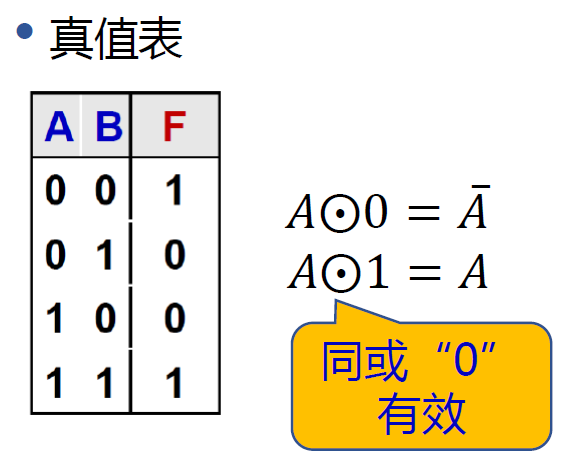
- \(A\odot0=\overline{A}\), \(A\odot 1 = A\)
- 同或中 1 对结果无影响
- 奇数个 0, 结果为 0, 偶数个 0, 结果为 1
- 典型芯片: 74LS266
- 应用: 等同比较器
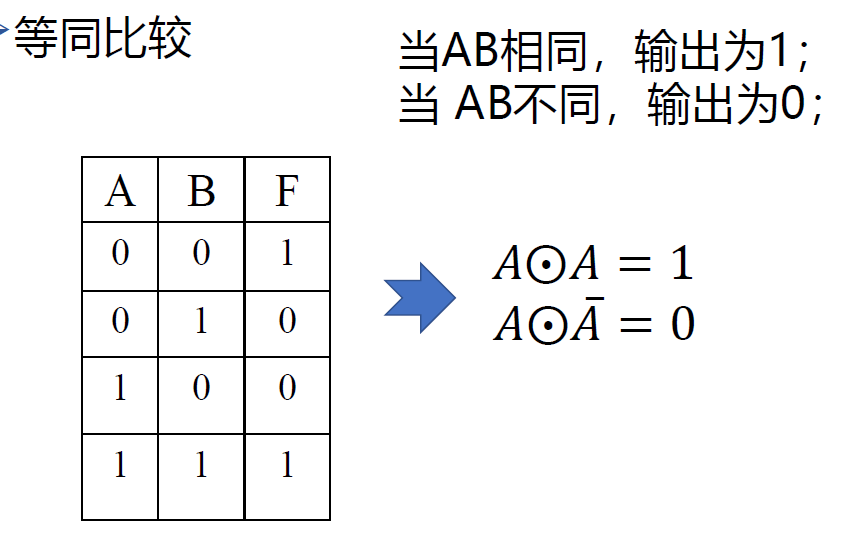
- 逻辑符号:
-
多个 1 或 0 同或/异或操作如何解
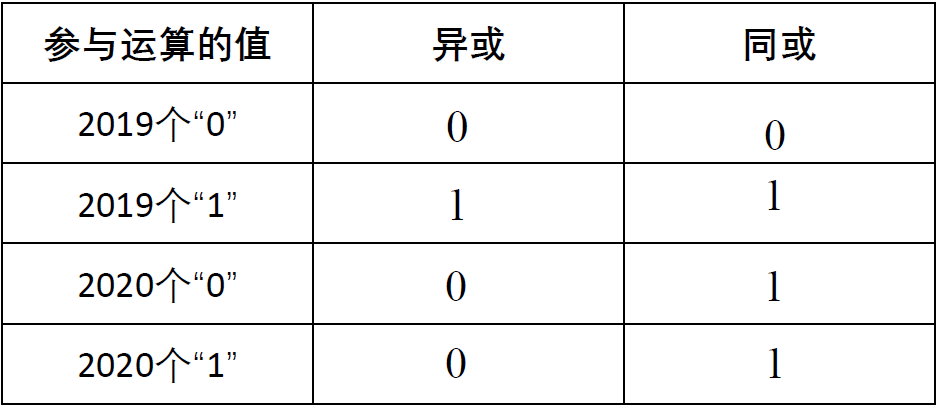
- 异或
- 0 对异或的结果没有影响, 结果依然是 0
- 奇数个 0(2019), 结果为 1; 偶数个 0(2020), 结果为 0
- 同或
- 1 对同或的结果没有影响, 结果依然是 1
- 奇数个 1(2019), 结果为 1; 偶数个 1(2020), 结果为 0
- 异或
2.1.3 逻辑函数的表示方法¶
-
描述逻辑函数的方法并不是唯一的, 他们之间可以很方便的相互转换
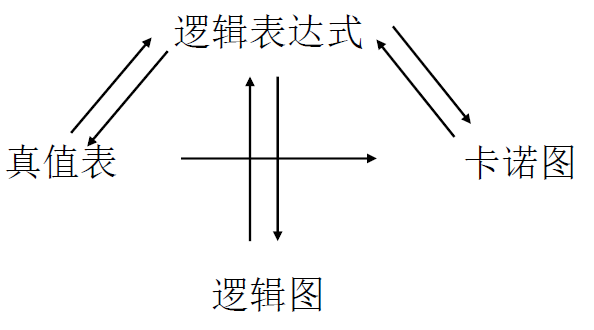
-
逻辑表达式 (基础)
- 例: \(F=AB+\overline{A}\ \overline{B}\) ; \(F=\overline{A(C+D)}+BE\)
- 逻辑表达式书写时要注意优先级问题
-
逻辑图
-
逻辑表达式->逻辑图
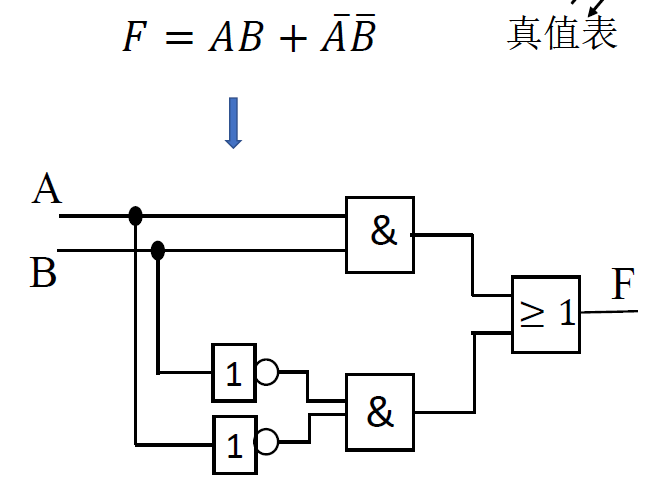
-
逻辑图->逻辑表达式
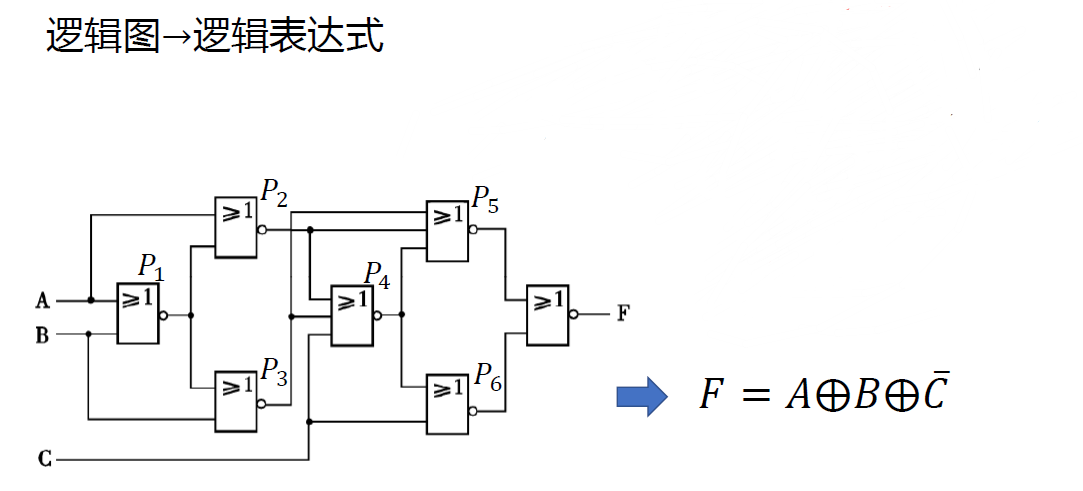
-
-
真值表
- 真值表由两部分组成,左边一栏列出变量的所有取值组合,右边一栏为逻辑函数值
- 为了不发生遗漏,通常各变量取值组合按二进制数码顺序给出。
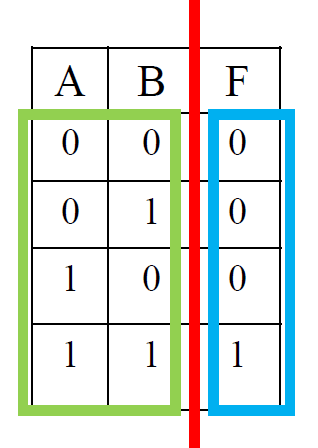
-
真值表和逻辑表达式的互相转换
-
逻辑表达式->真值表: 穷举(注意排序)
-
真值表->逻辑表达式 (在数逻中, 使用主析构范式)
1. 从真值表中找到使 F=1 的输入变量取值
2. 将每一组变量取值写成对应的乘积项: 取值为 0 的变量写成反变量, 取值为 1 的变量写成原变量(取得最小项)
3. 将乘积项相加, 得到最后的表达式
4.
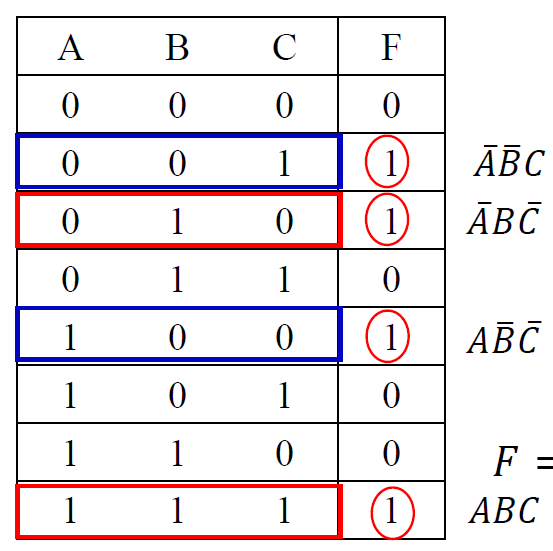
$F=\overline{A}\ \overline{B}C + \overline{A}\ B\overline{C} + A\overline{B}\ \overline{C}+ABC$
-
-
最大项和最小项
-
最小项: 与项 , 用mi表示, i 为让==与项值为 1== 的变量组合
最大项: 或项 , 用 Mi表示, i 为让==或项值为 0== 的变量组合
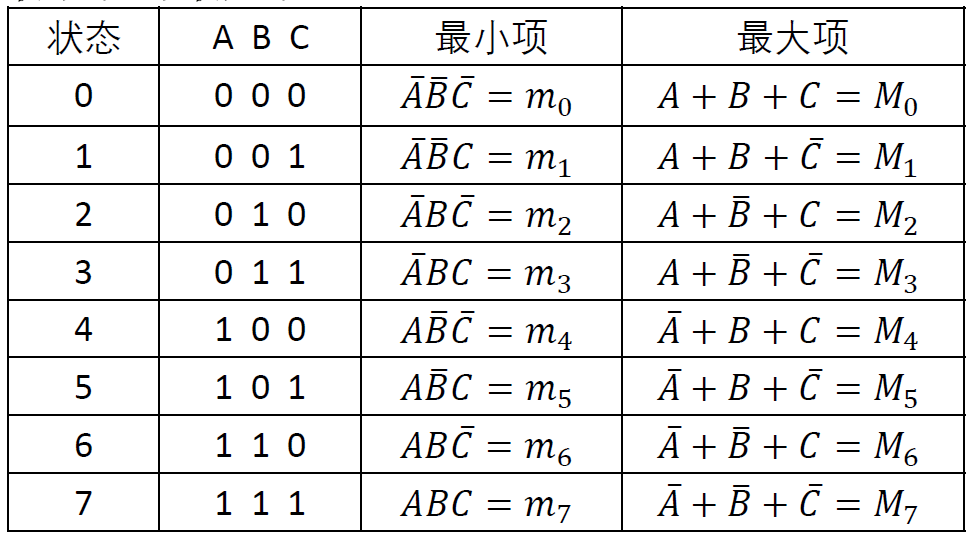
-
最小项表达式:
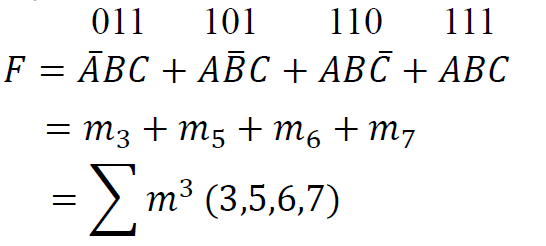
最大项表达式:

-
-
\(M_i = \overline{m_i}\)
- \(Y = \sum_i m_i = \prod_{k\not=i}M_k\)
-
-
2.2 逻辑代数定理和规则¶
2.2.1 公理¶
-
常量运算 (注意, 0 和 1 是真假, 而非数值)
- \(0+0=0\); \(0+1=1\); \(1+1=1\)
- \(0×0=0\); \(0×1=0\); \(1×1=1\)
- \(\overline{0} = 1\); \(\overline{1}=0\)
-
公理(与普通代数类似)
- 交换律:\(A+B=B+A\); \(A\cdot B=B\cdot A\)
- 结合律: \((A+B)+C = A+(B+C)\); \((A\cdot B)\cdot C=A\cdot(B\cdot C)\)
- 分配律 : - \(A+(B\cdot C) = (A+B) \cdot (A+C)\); (与普通的乘法对加法的分配律不同) - \(A\cdot(B+C) = A\cdot B + A\cdot C\)
- 01 律: - \(A+0=A\), \(A+1=1\) - \(A\cdot 0=0\), \(A\cdot 1=A\)
- 互补律: - \(A+\overline{A} = 1\) - \(A\cdot \overline{A}=0\)
注意: 以上公理不适用于普通代数
2.2.2 基本定理¶
- 重叠律: \(A+A=A\); \(A\cdot A=A\)
-
吸收律 (分配律的特殊情况)
- \(A+A\cdot B = A\)
- \(A\cdot(A+B) = A\)
-
消除律 (分配律的特殊情况)
- \(A+\overline{A}\cdot B=A+B\) (证明通过加法对乘法的分配律)
- \(A\cdot(\overline{A}+B) = A\cdot B\)
-
双重否定律: \(\overline{\overline{A}} = A\)
- 反演律(德.摩根定律) \(\overline{A+B} = \overline{A}\cdot\overline{B}\); \(\overline{A\cdot B} = \overline{A} + \overline{B}\)
-
包含律 :
-
\(A\cdot B+ \overline{A}\cdot C + B\cdot C = A\cdot B+ \overline{A}\cdot C\)
- 证明: \(A\cdot B+ \overline{A}\cdot C + B\cdot C\cdot(A + \overline{A})\) (引入冗余项\((A + \overline{A})\))
- \((A+B)\cdot(\overline{A}+C)(B+C) = (A+B)\cdot(\overline{A}+C)\)
- 拓展: \(A\cdot B+ \overline{A}\cdot C + B\cdot C\cdot D = A\cdot B+ \overline{A}\cdot C\)
-
2.2.3 规则¶
- 代入规则
- 定义:任何含有变量 A 的逻辑等式,如果将所有出现 A 的位置都代之以同一个逻辑函数 F,则等式仍然成立。
- 意义:利用这条规则可以将逻辑代数公理. 定理中的变量用任意函数代替,从而==推导出更多的等式== 。
- 反演规则(摩根定理)
- 如果将逻辑函数表达式 F 中所有的“•”变成“+”,“+”变成“•”,“0”变成“1”,“1”变成“0”,原变量变成反变量,反变量变成原变量,并保持原函数中的==运算顺序不变== ,则所得到的新的函数为原函数 F 的反函数\(\overline{F}\)。
- 反演规则 VS 反演律: 反演规则是反演律的推广, 本质一样, 但是使用方法和适用场景有所不同
- \(\overline{X_{1}X_{2}...X_{n}} = \overline{X_1}+\overline{X_2}+...+\overline{X_n}\)
- \(\overline{X_{1}+X_{2}+...+X_{n}} = \overline{X_1}\cdot\overline{X_2}\cdot...\cdot\overline{X_n}\)
-
对偶规则
- 如果将逻辑函数表达式 F 中所有的“•”变成“+”,“+”变成“•”,“0”变成“1”,“1”变成“0”,并保持原函数中的运算顺序不变,则所得到的新的逻辑表达式称为函数 F 的对偶式,并记作F '。
-
取反对对偶没有影响, 所以遇到反时可以直接保留
- 应用: 若两个逻辑函数表达式 F 和 G 相等,则其对偶式 F’ 和 G’也相等。即若 F=G,那么 F’=G’。
- 利用对偶规则可以使定理. 公式的证明减少一半。
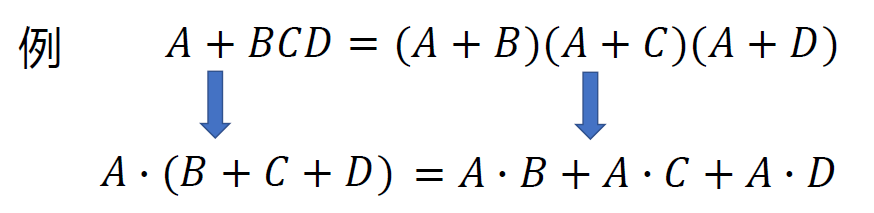
2.4 逻辑函数化简¶
-
逻辑函数的基本形式
- 按照逻辑函数表达式中乘积项的特点以及各个乘积项之间的关系, 可分为 5 种一般形式
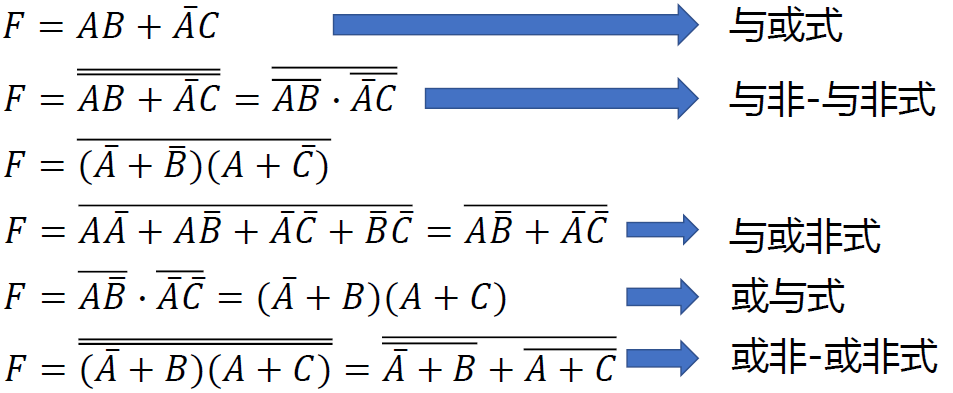
-
逻辑函数化简的目的----最简形式
-
函数表达式一般化简成 最简与或式 , 其最简应该满足两个条件
-
表达式中的"与项"个数最少
-
在满足 1 的前提下, 每一个"与项"中的变量个数最少
-
例:
\(Y=A+\overline{A}C+AB\)
\(\Rightarrow Y=A+C\)
-
- 三个变量,四个与项,不是最简
-
2.4.1 代数化简法¶
- 并项法: \(AB+A\overline{B}=A\)
- A, B 可以是任意复杂的逻辑公式
- \(Y=ABC+AB\overline{C}+A\overline{B}\ =AB + A\overline{B}\ =A\)
- 吸收法 \(A+AB=A\)
- A, B 可以是任意复杂的逻辑公式
- \(Y= (\overline{A\overline{B}} + C)ABD +AD\ =AD\)
- 此处 A 是 AD, B 是\((\overline{A\overline{B}} + C)B\)
- 消去法 \(A+\overline{A}B = A+B\) , \(AB + \overline{A}C + BC = AB+\overline{A}C\)
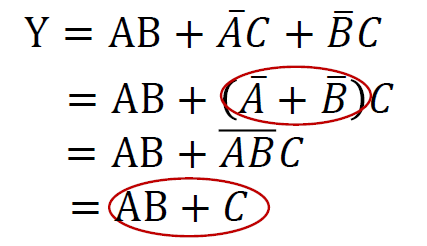
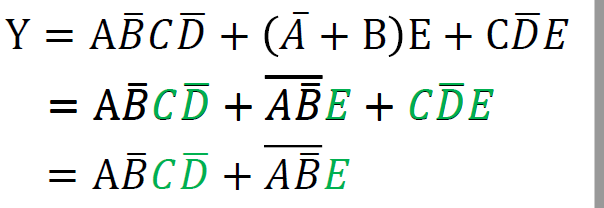
- 善用摩根定律, 构造取反的部分
- 配项法 \(A+A=A\), \(A+\overline{A} = 1\)
- A 可以任意复杂的逻辑式
2.4.2 卡诺图化简法¶
-
标准与或式(最小项表达式)(主析取范式): 由若干个最小项相或构成
标准或于式(主析取范式): 由若干个最大项相与构成
- 任何一个逻辑函数都可以表示成唯一的最小项表达式
- 如: \(F(A, B, C)=\overline{A}\ \overline{B}C + \overline{A}B\overline{C} + A\overline{B}\ \overline{C} + ABC\)
- \(001(1)+010(2)+100(4)+111(7)\)
- 最小项表达式: \(\sum m^{3}(1, 2, 4, 7)\)
- 最大项表达式: \(\prod M^3(0, 3, 5, 6)\)
-
逻辑函数形式转换
- 利用逻辑代数的公理, 定理和规则可以将任意逻辑函数表达式转为标准与或式
- 与或式 -> 标准与或式: 利用互补律进行展开, 缺什么补什么
- \(X = X\cdot(Y + \overline{Y})\)
- 或与式 -> 标准与或式: ① 缺什么补什么; ② 转为与或式后再按照与或式处理
- \(X=(X+Y)\cdot(X+\overline{Y})\)
-
卡诺图------最小项的图形表示法
- 卡诺图: 将 n 个输入变量的 2𝑛 个最小项各用一个小方格表示,把它们排成矩阵,并且==保证相邻的最小项只有一个变量不同== (格雷码),所得到的阵列图就是 n 变量的卡诺图。
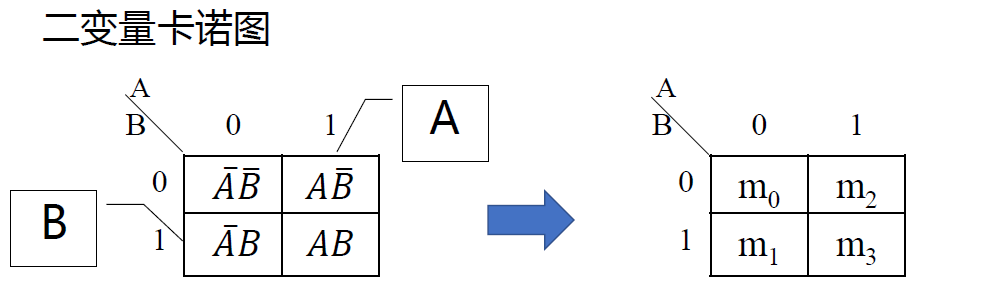
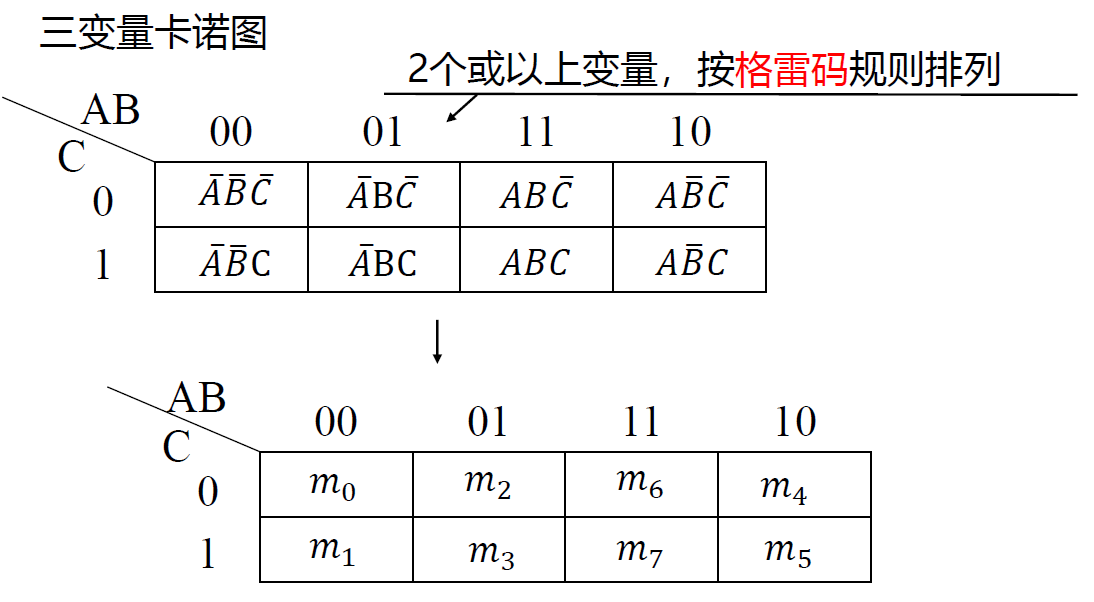
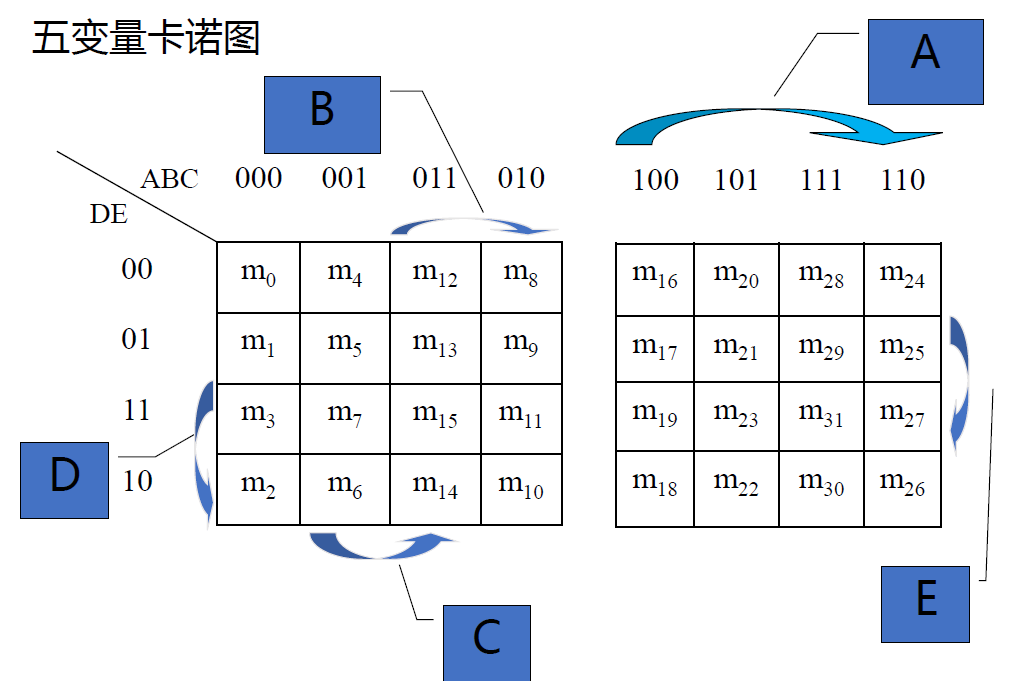
- 五变量的卡诺图并不是按照格雷码排序, 而是经过翻折
卡诺图化简法¶
- 画卡诺圈: 通过卡诺圈圈住相邻的 1 的小方格
- 注意: 卡诺圈里的小方格的个数必须为 2m
- 卡诺图中什么位置的方格是相邻的 1. 紧挨着的 2. 行列首尾的 3. 对称的
- 卡诺圈里的小方格越多越好 - 卡诺圈里方格数与消去的变量的关系: 2m个方格消去 m 个变量
- 观察卡诺图, 写出卡诺图表示的与项
- 观察每个卡诺图对应的行左&列上
- 变量取值不同--消去
- 变量取值相同--保留
- 将所有的与项相加, 并==检查== 是否遗漏为 1 的方格
- 注意点
- 不同的圈法, 可能得出不同的最简结果
- 如果某一个卡诺圈所有的"1"均被别的圈圈过, 则此卡诺圈表示的与项是==多余== 的 - 画卡诺圈时应该先从圈法最少的方格开始
- 当卡诺图中 0 较少时, 可以采用非来得到最简式
带无关项的卡诺图化简¶
- 无关项:不存在的或无意义的取值组合
- 卡诺图化简时对无关项的处理
- 根据化简的需要, 无关项可 0 可 1
- 满足卡诺圈中"1"(或"0")的数量最多的前提下, 尽量利用无关项
第三章 集成门电路¶
3.1 门电路¶
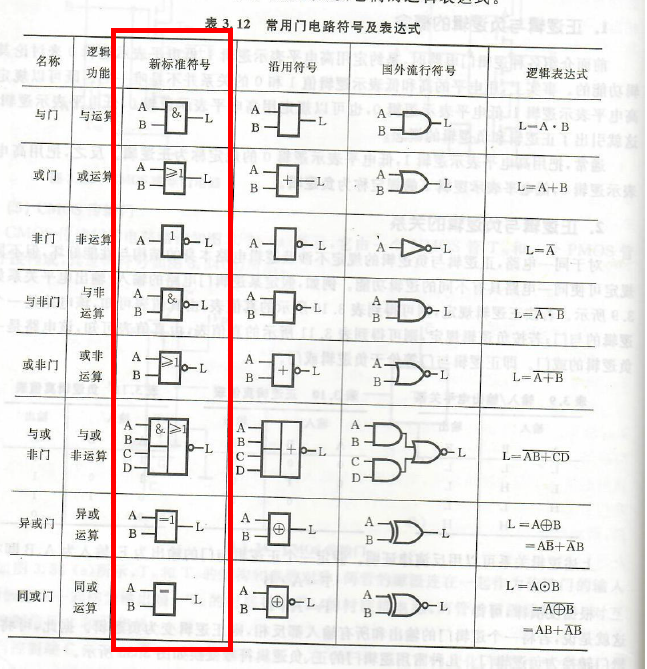
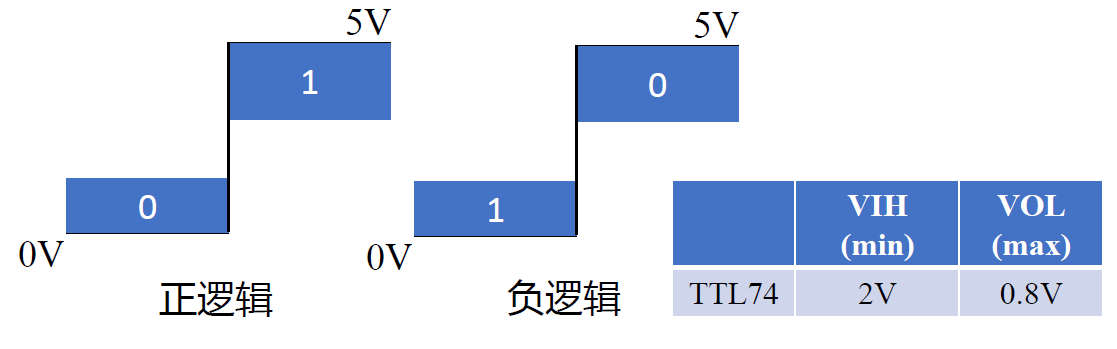
3.2 正负逻辑约定¶
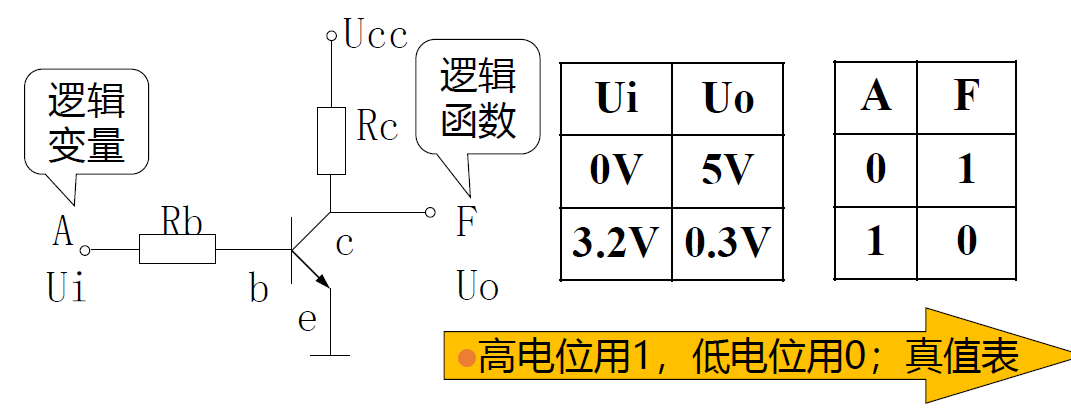
- 正逻辑: 门电路的输入, 输出电压定义为 低电位->0; 高电位->1
- 负逻辑: 门电路的输入, 输出电压定义为 低电位->1; 高电位->0
3.3 分立元件门电路¶
-
二极管开关特性: 正向导通, 反向截止
-
三极管开关特性:
- 饱和导通: 基极电流增大, 集电极电流不再增大
- 截止: 三极管各极电流几乎为 0
-
二极管**与门 **
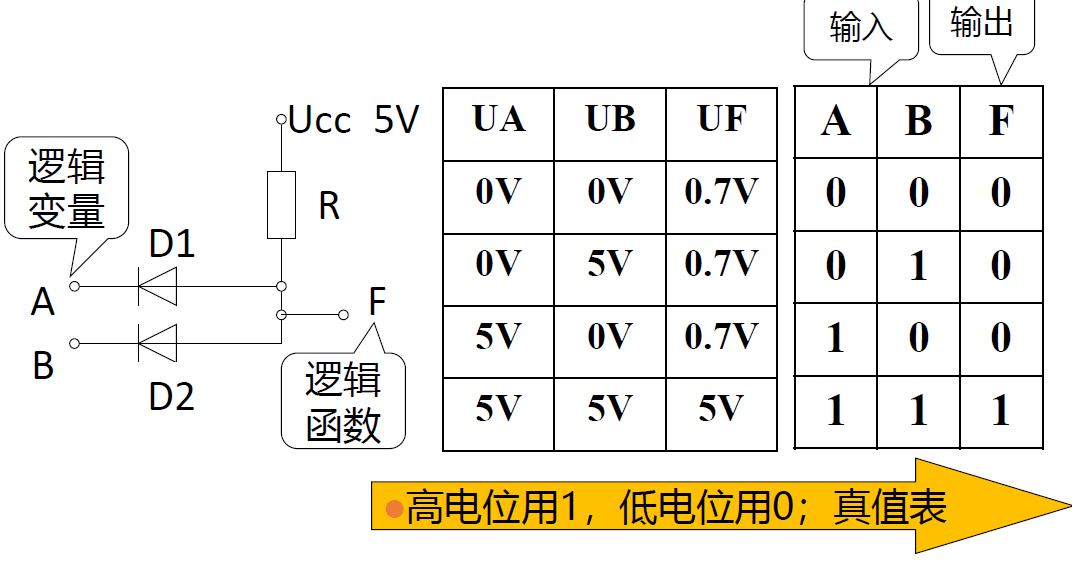
-
二极管或门
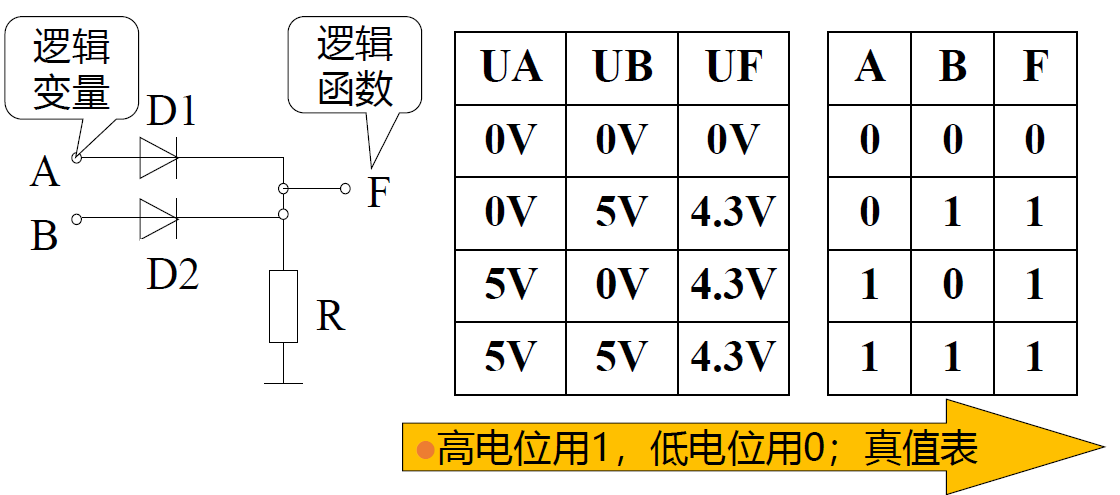
-
二极管非门
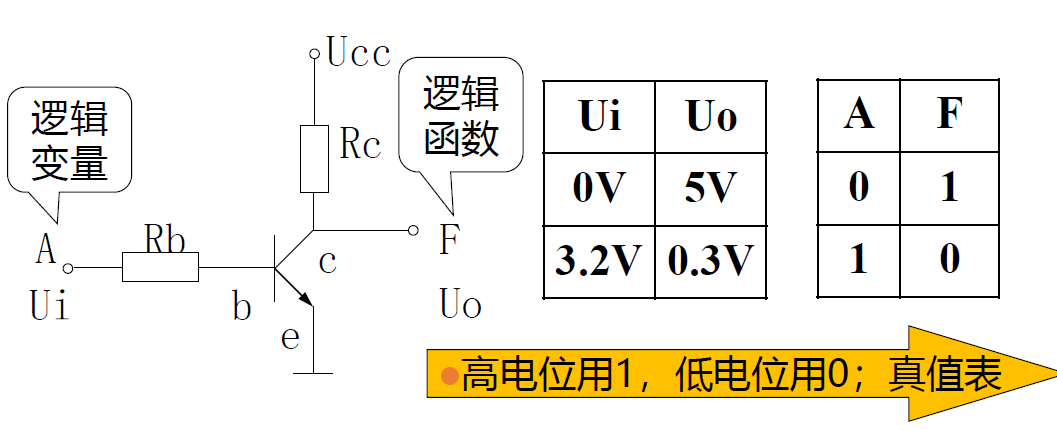
3.4 TTL 逻辑门电路¶
-
三极管非门
-
与非门
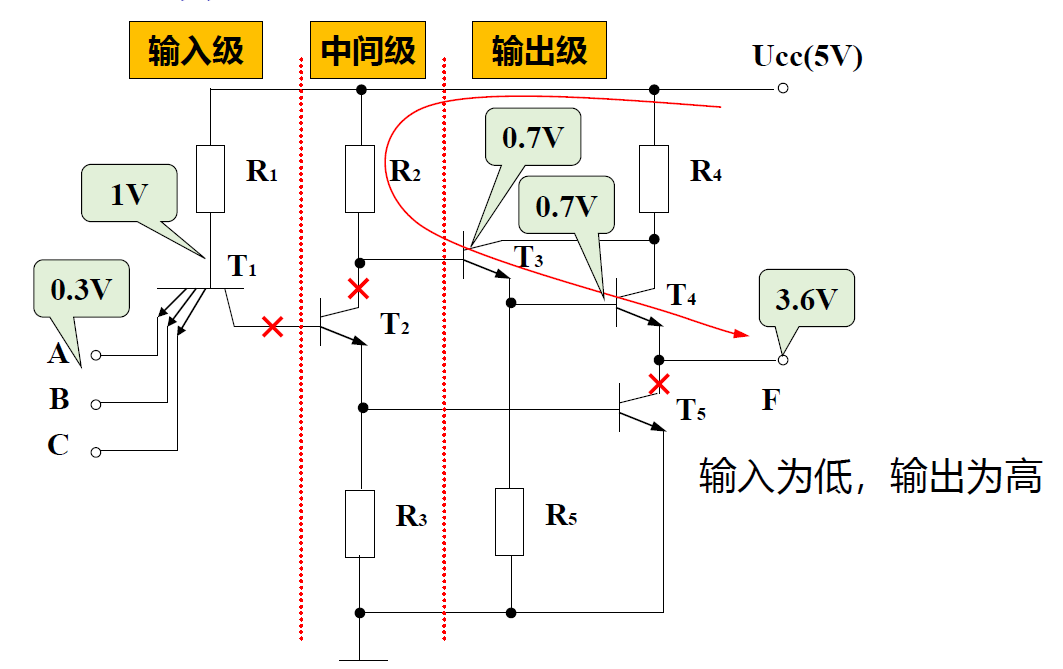
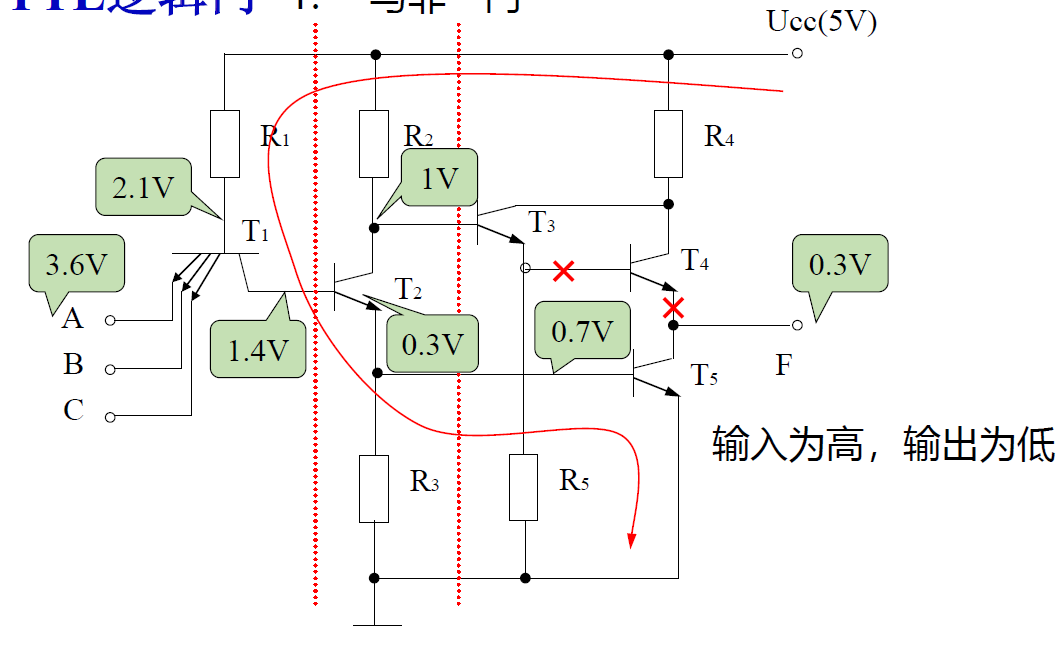
-
与非门常用芯片
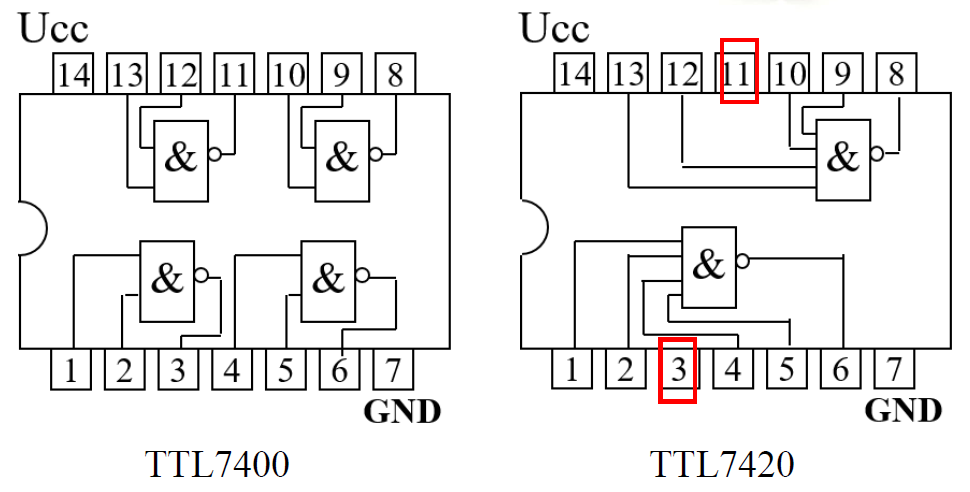
-
-
3.5 OC 门和三态门¶
-
集电极开路门(OC 门)
- OC 门是一种输出端可以相互连接的特殊逻辑门
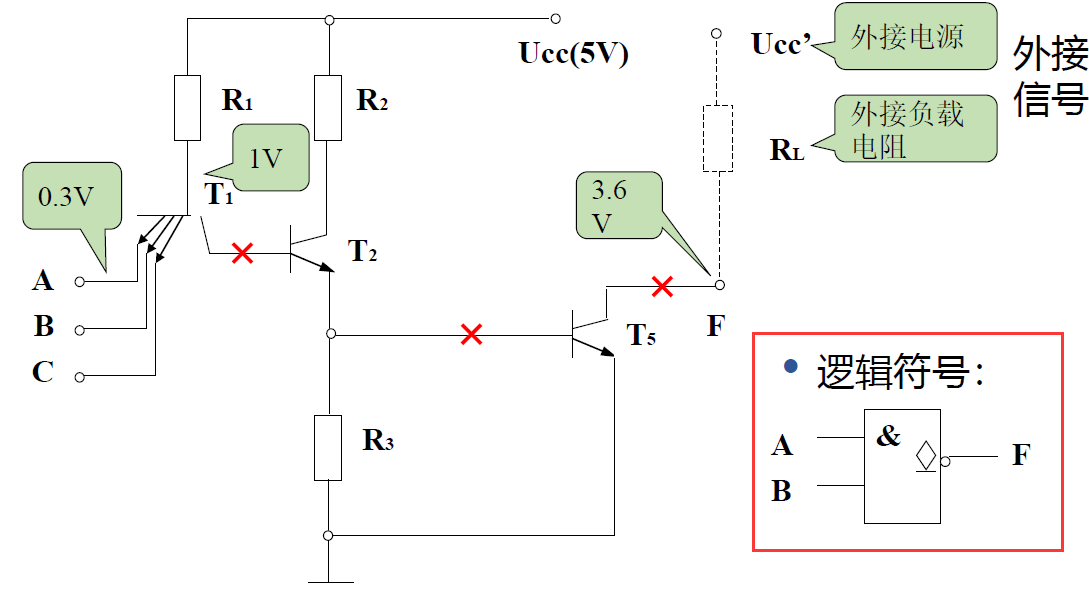
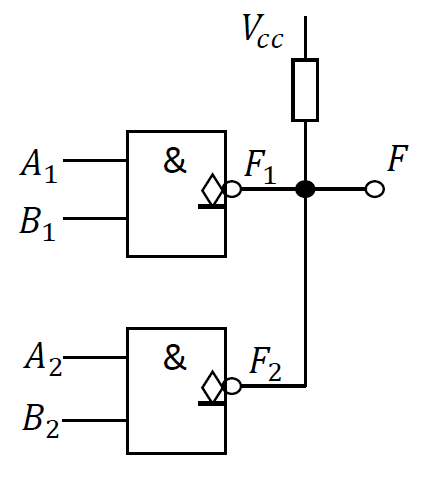
-
线与逻辑: 两个与非门输出相与
- 只要有一个门输出为低电平, 输出 F 便为低电平
- 仅当两个门输出都为高电平, 输出 F 才是高电平
- \(F=F_1\cdot F_2 = \overline{A_1B_1}\cdot\overline{A_2B_2}\)
-
三态输出门(TS 门)
-
三种输出状态: 输出高电平, 输出低电平, 高阻状态
前两者为工作状态, 后一种为禁止状态
-
EN=1 时, 二极管反偏, 电路功能与普通与非门相同
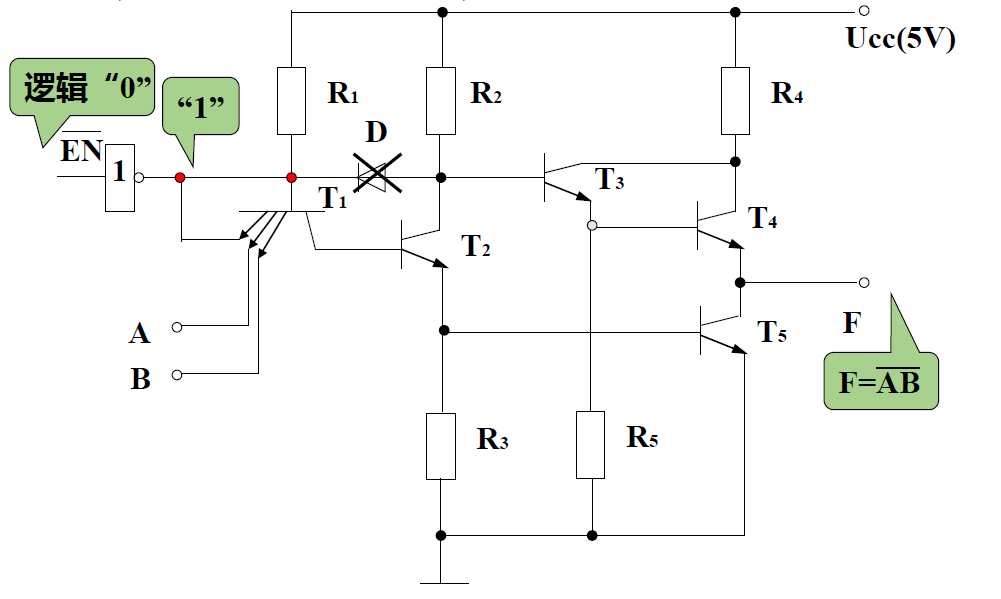
-
EN=0 时, 二极管导通, 输出电压与输入无关, 即处于高阻状态
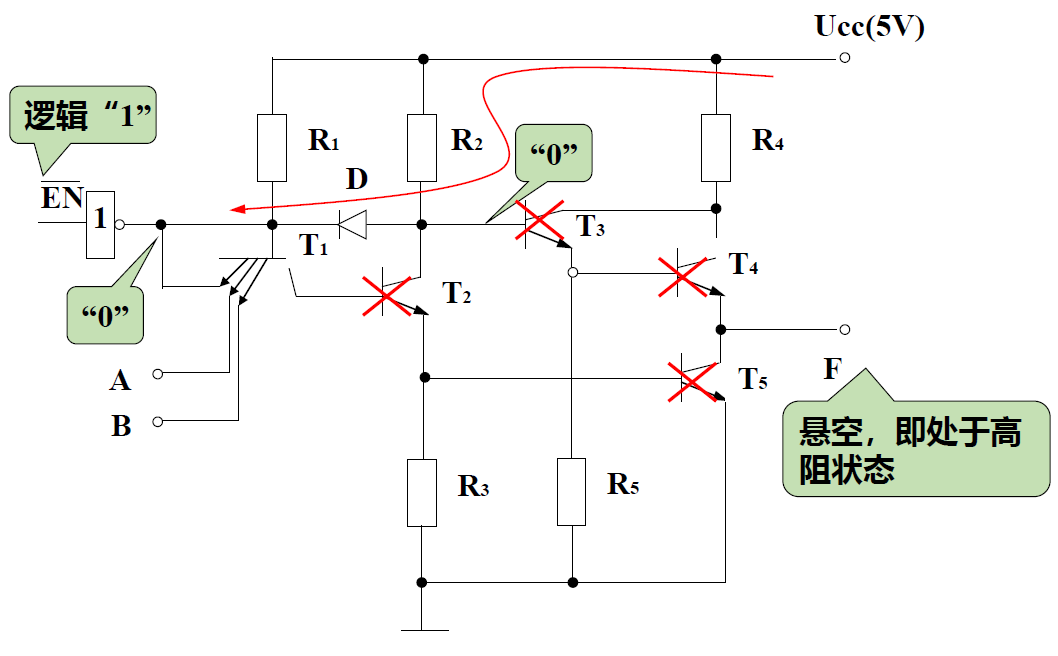
-
第四章 组合逻辑电路¶
-
组合逻辑电路学习结构
- 组合逻辑电路分析
- 组合逻辑电路分析
- 中规模组合逻辑电路芯片
- 加法器
- 译码器 (编码器略)
- 选择器
- 组合逻辑电路: 任何时刻电路的输出状态只取决于该时刻的输入状态, 而与该时刻以前的电路状态无关
- 单向性, 无反馈
- 无记忆单元 (无触发器)

4.1 组合逻辑电路分析¶
\(任务: 已知逻辑电路\stackrel{确定}{\longrightarrow} 逻辑功能\)¶
- 逻辑电路功能描述可用表达式. 卡诺图. 真值表等多种方法,这里特指用概括的文字进行功能描述。
-
目的: ① 了解电路功能 ② 改进电路设计
-
方法:
①写表达式 ②化简变换 ③列真值表 ④功能描述
-
例一: 分析下图逻辑功能
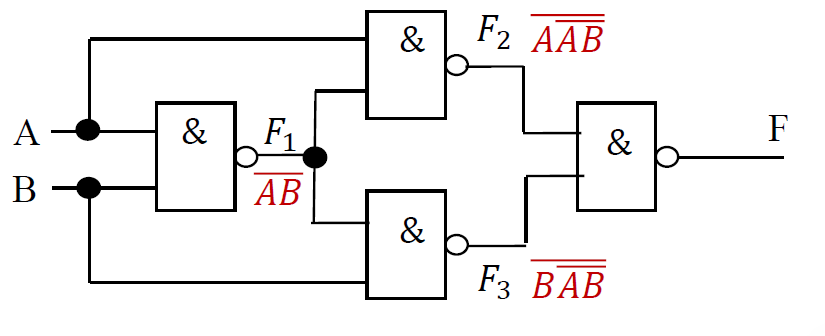
-
写出逻辑表达式 \(F = F_2F_3 = \overline{\overline{A\overline{AB}} \cdot \overline{B \overline{AB}}}\)
-
应用逻辑代数法化简
- \(F = F_2F_3 = \overline{\overline{A\overline{AB}} \cdot \overline{B \overline{AB}}}\)
$=A\cdot \overline{AB} + B\cdot \overline{AB}$ $= A\cdot(\overline{A} + \overline{B}) + B\cdot (\overline{A} + \overline{B})$ $= A\overline{B} + \overline{A}B$ -
列逻辑状态表
-
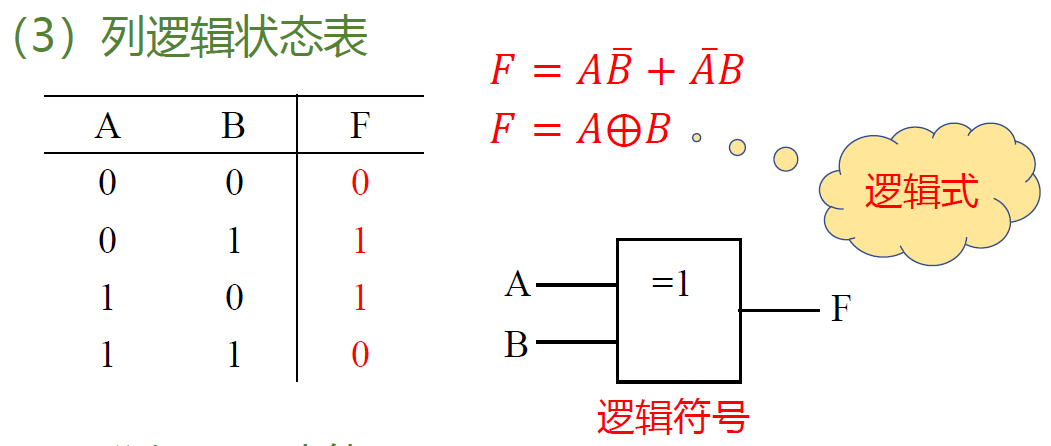
-
分析逻辑功能: 输入相同输出为“0”,输入相异输出为“1”,称为“异或”逻辑关系。这种电路称为“异或”门。
-
-
例二: 分析逻辑功能
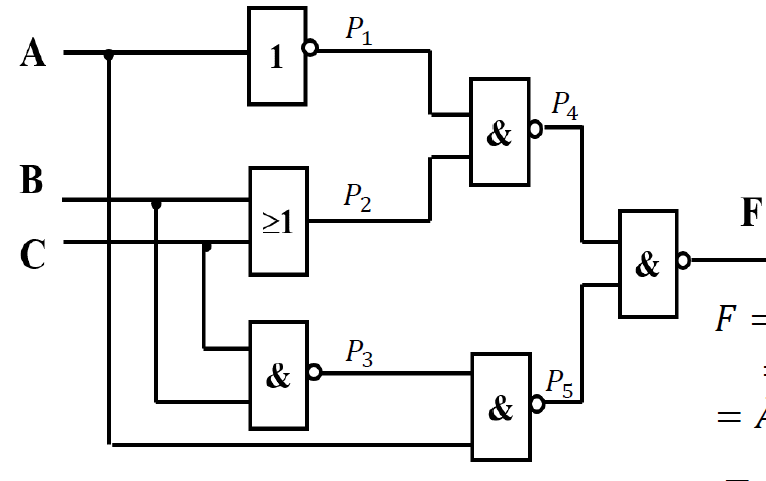
-
应用逻辑代数化简法
- \(P_1 = \overline{A}\)
- \(P_2 = B+C\)
- \(P_3 = \overline{BC}\)
- \(P_4 = \overline{P_1P_2}\)
- \(P_5 = \overline{P_3A}\)
- \(F = \overline{P_4P_5} = \overline{P_4} + \overline{P_5} = P_1P_2 + P_3A\)
$=\overline{A}B + \overline{A}C + A\overline{B} + A\overline{C}$ $=A\oplus B + A\oplus C$ -
列逻辑状态表
-
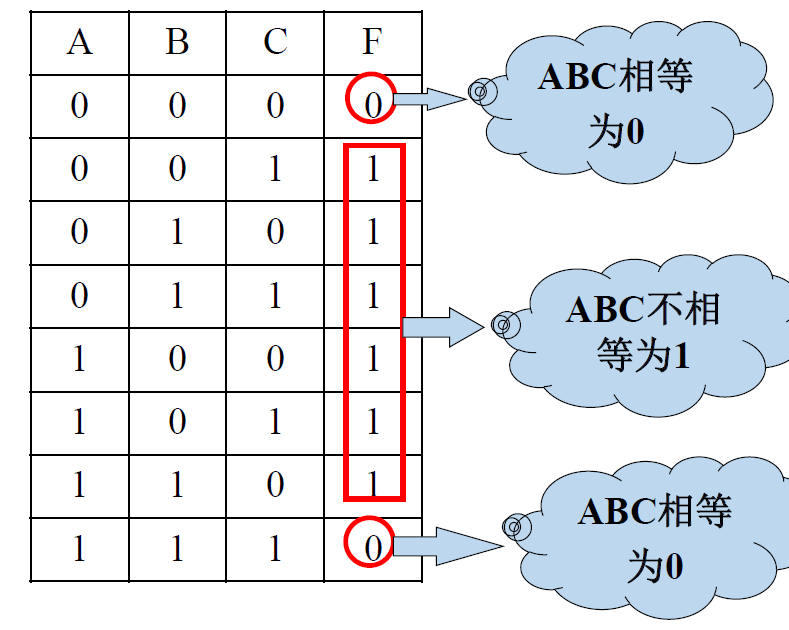
-
分析逻辑功能: 不一致判别功能
-
-
逐级电平推导法 (逆向推导)
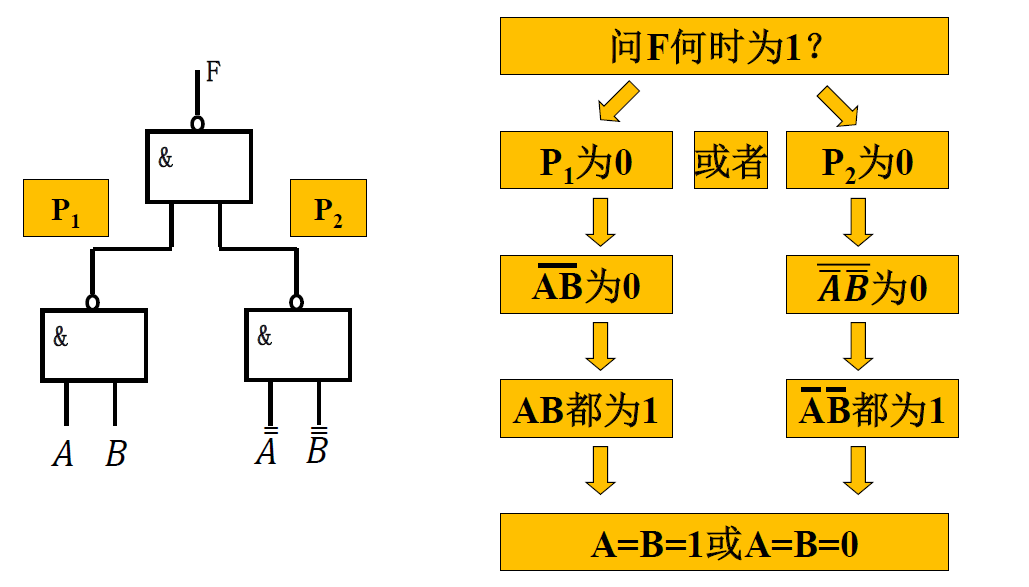
4.2 组合逻辑电路的设计¶
\(任务: 根据逻辑功能要求\stackrel{设计}\longrightarrow逻辑电路图\)¶
-
设计步骤
- 根据逻辑要求, 列出真值表 - 注意: 列真值表时 要进行逻辑变量假设 - 假设结果如果是数字, 用一个
- 由真值表写出逻辑表达式
- 化简和变换逻辑表达式 ----卡诺图化简法
- 画出逻辑电路图
-
例一 : 某工厂有A. B. C三个车间和一个自备电站,站内有两台发电机G1和 G2。G1的容量是 G2的两倍。如果一个车间开工,只需 G2,运行即可满足要求;如果两个车间开工,只需 G1运行;如果三个车间同时开工,则 G1和 G2均需运行。
现根据碳中和节能减排要求,设计控制 G 和 G2 节能运行的逻辑图(用与非门实现)。
-
根据逻辑要求进行逻辑变量假设
- 首先假设逻辑变量. 逻辑函数取“0”. “1”的含义。 - 设:A. B. C 分别表示三个车间的开工状态:开工为“1”,不开工为“0” - G1和 G2运行为“1”,不运行为“0"
-
根据逻辑假设列出真值表
- 逻辑要求:如果一个车间开工,只需 G 运行即可满足要求;如果两个车间开工,只需 G 运行;如果三个车间同时开工,则 G1 和 G 均需运行 -
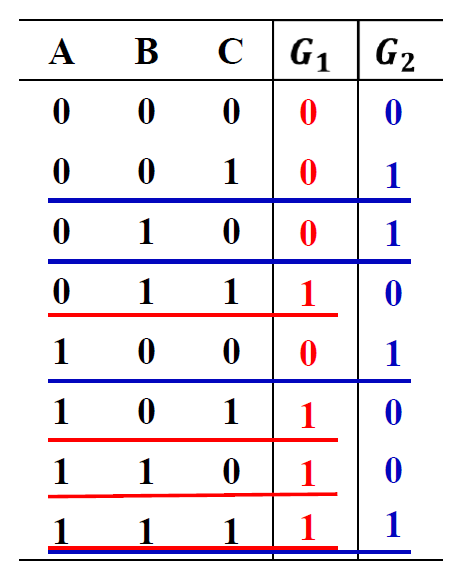
-
由真值表写出逻辑式
- \(G_1 = \overline{A}BC+A\overline{B}C + AB\overline{C}+ABC\) - \(G_2 = \overline{A}\,\overline{B}C + \overline{A}B\overline{C} + A\overline{B}\,\overline{C} + ABC\)
-
卡诺图化简
- \(G_1 = AB+BC+AC\)
<img src="数字电路与逻辑设计.assets\image-20221127180113234.png" alt="image-20221127180113234" style="zoom:33%;" />- \(G_2 = \overline{A}\,\overline{B}C + \overline{A}B\overline{C} + A\overline{B}\,\overline{C} + ABC\) (不可化简)
<img src="数字电路与逻辑设计.assets\image-20221127180129044.png" alt="image-20221127180129044" style="zoom:33%;" /> -
转换为“与非-与非”逻辑表达式
- \(G_1 = \overline{\overline{AB+BC+AC}} = \overline{\overline{AB}\cdot \overline{BC} \cdot\overline{AC}}\) - \(G_2 = \overline{\overline{\overline{A}\,\overline{B}C + \overline{A}B\overline{C} + A\overline{B}\,\overline{C} + ABC}} = \overline{\overline{\overline{A}\,\overline{B}C }\cdot \overline{\overline{A}B\overline{C} }\cdot \overline{A\overline{B}\,\overline{C} }\cdot \overline{ABC}}\)
-
画出逻辑电路图
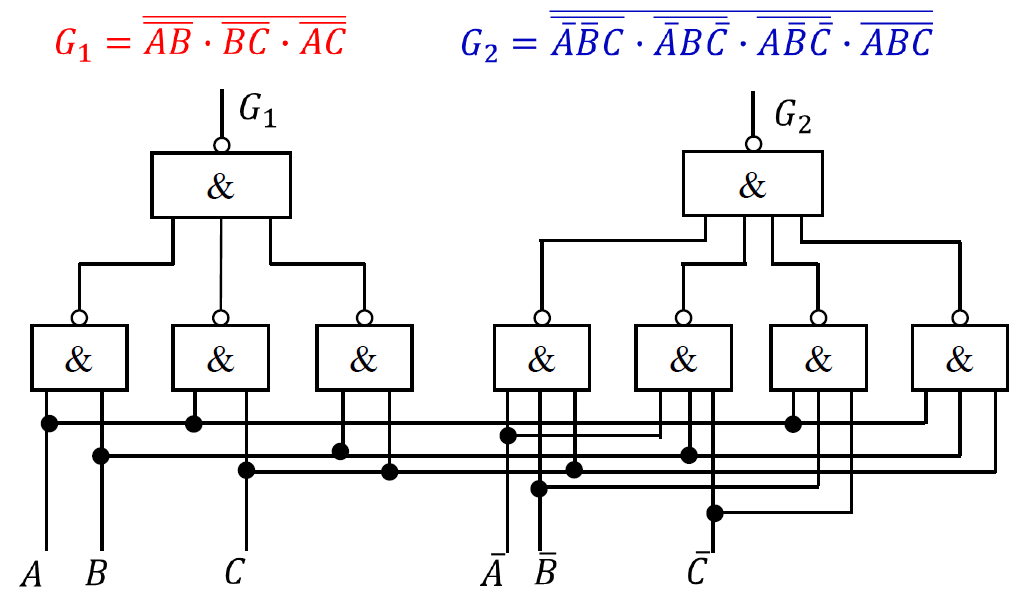
-
-
例二

-
例二 plus

4.2.* 带无关条件的电路设计¶
复习一下编码的冗余值, 在这里, 冗余值即为无关条件
-
真值表分析

-
卡诺图化简
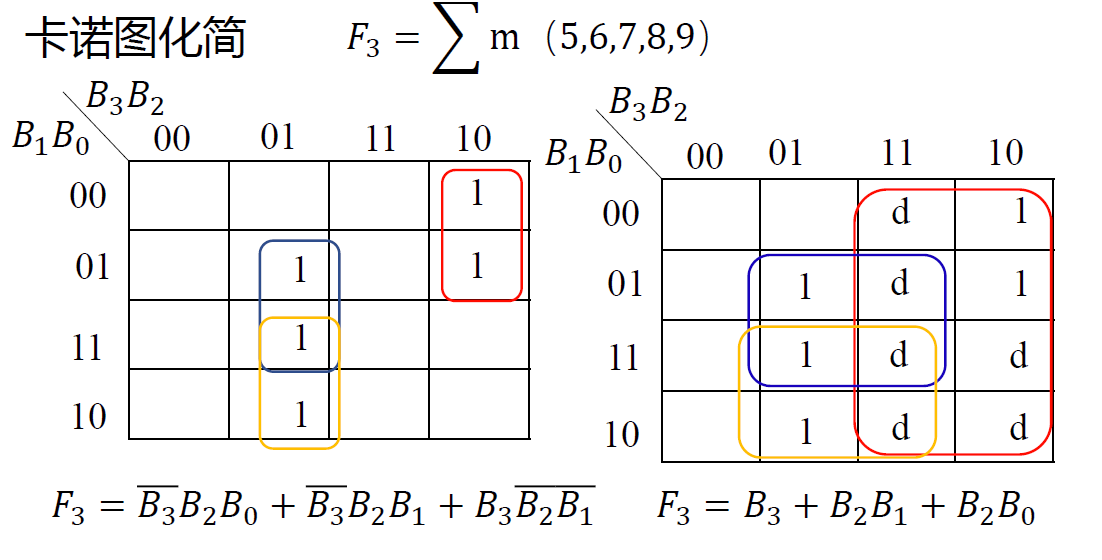
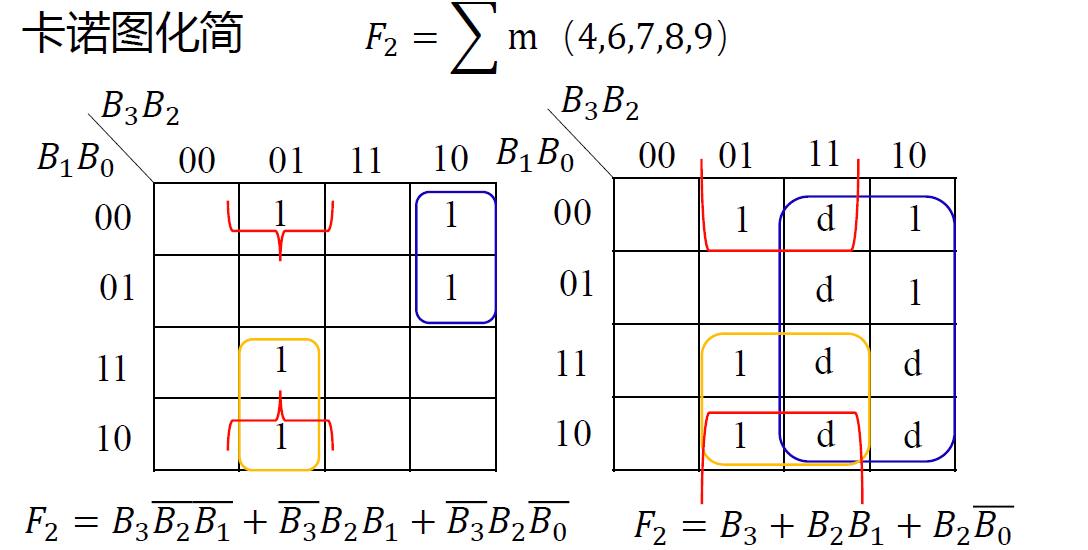
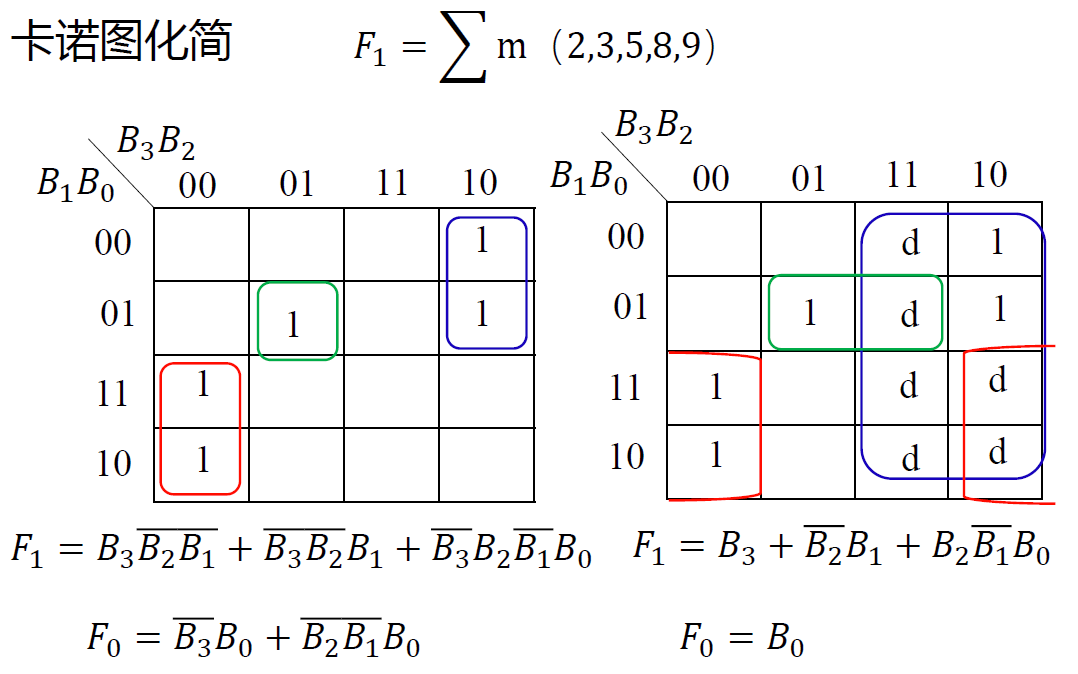
-
画出电路图
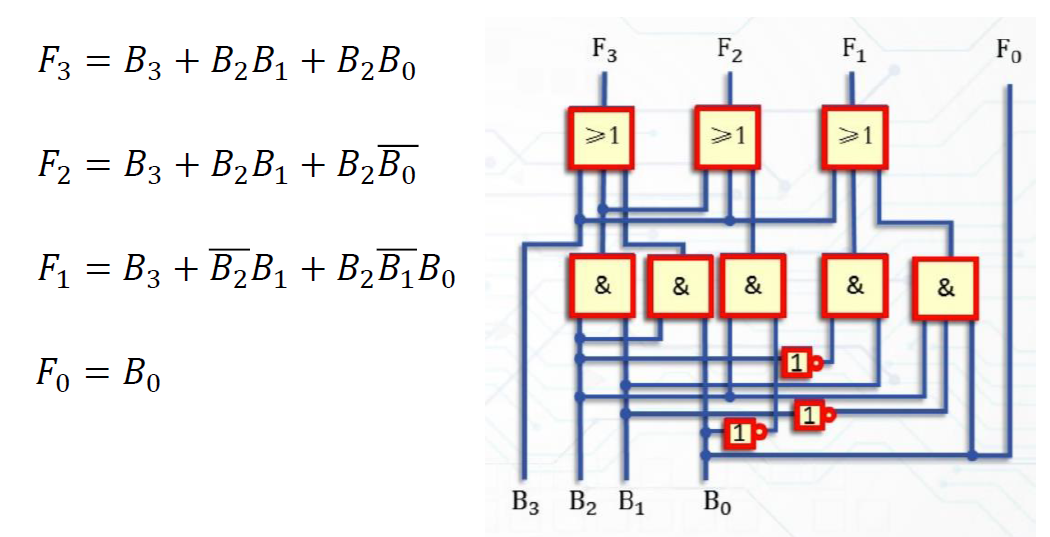
4.3 中规模组合逻辑电路芯片¶
4.3.1 加法器¶
一. 半加器(Half adder)¶
-
功能: 对==两个== 1 位 二进制数执行相加运算
-
结构:
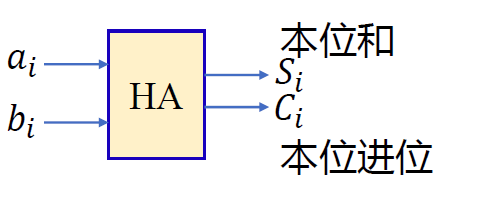
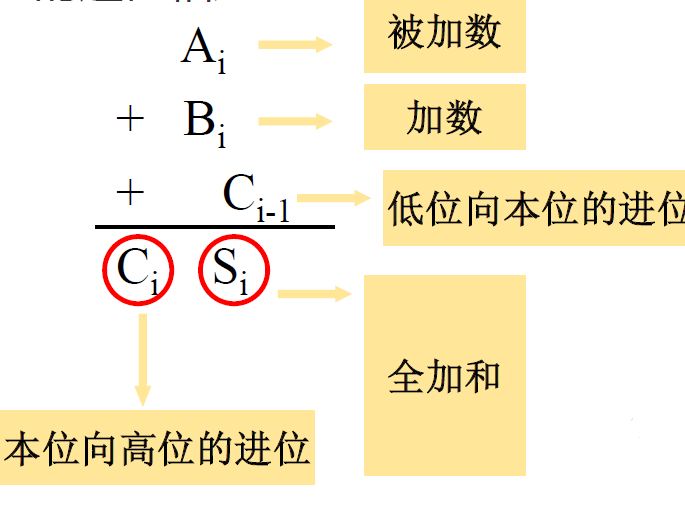
- $a_i $: 数 a 的第 i 位
- \(b_i\) : 数 b 的第 i 位
- \(S_i\): 本位和, 加法后第 i 位的结果
- \(C_i\) : 本位进位, 加法后第 i 位的进位
-
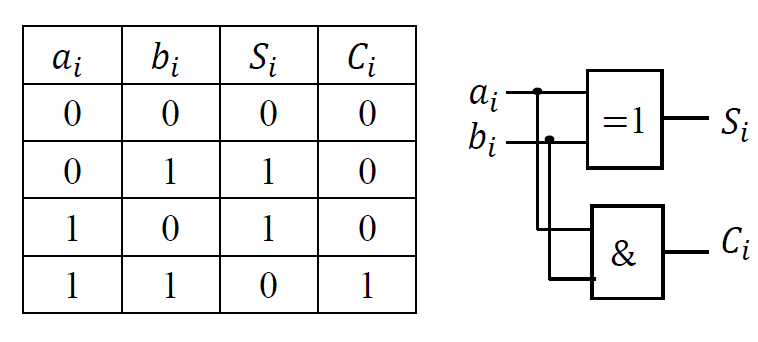
计算: \(\begin{cases}S_i = a_i\oplus b_i\\ C_i = a_ib_i\end{cases}\)
-
半加器的逻辑符号:
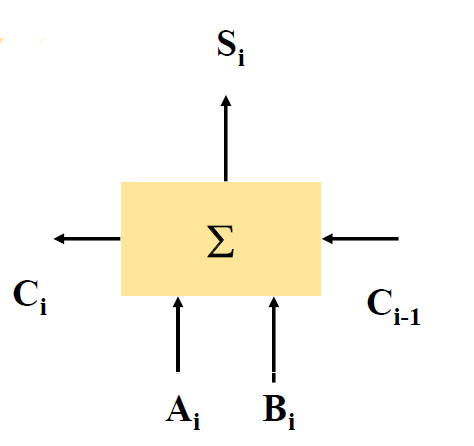
二. 全加器(Full adder)¶
-
功能: 将本位的两个一位二进制数(\(a_i, b_i\)) 和来自地位的进位(\(C_{i-1}\))相加
-
全加器的实现
- 真值表 → 卡诺图 → 表达式
-
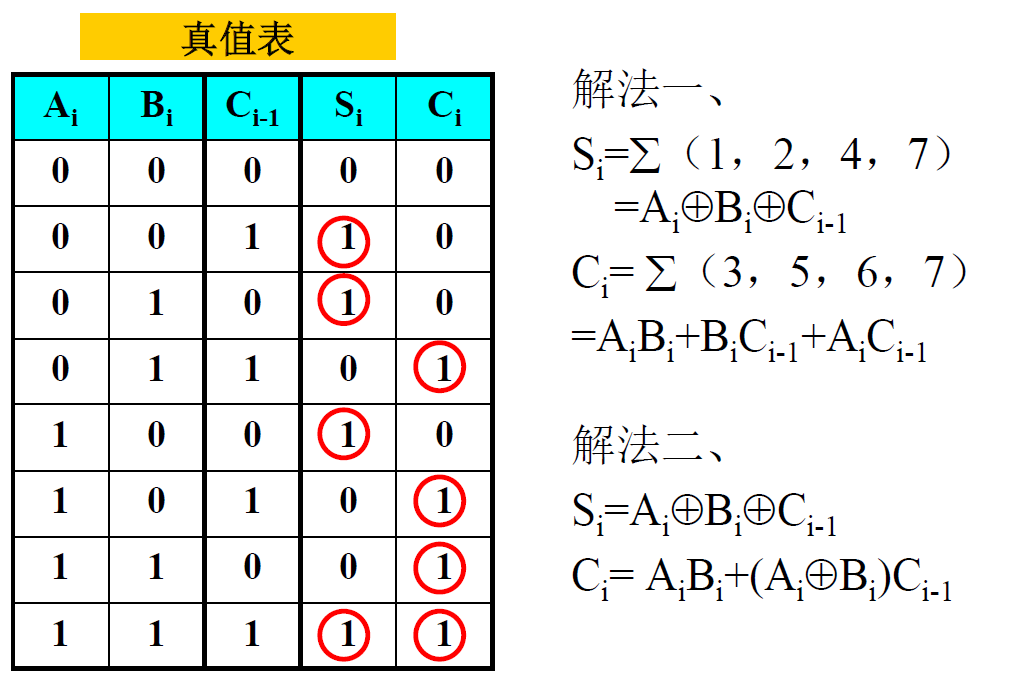 - 全加器: \(S_i = \sum m^3(1,2,4,7)\quad C_i = \sum m^3(3,5,6,7)\)
- 逻辑符号:
- 全加器: \(S_i = \sum m^3(1,2,4,7)\quad C_i = \sum m^3(3,5,6,7)\)
- 逻辑符号: 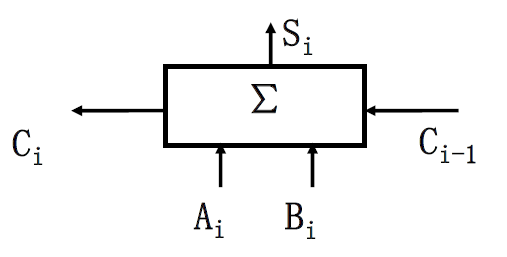 - 逻辑电路:
- 逻辑电路: 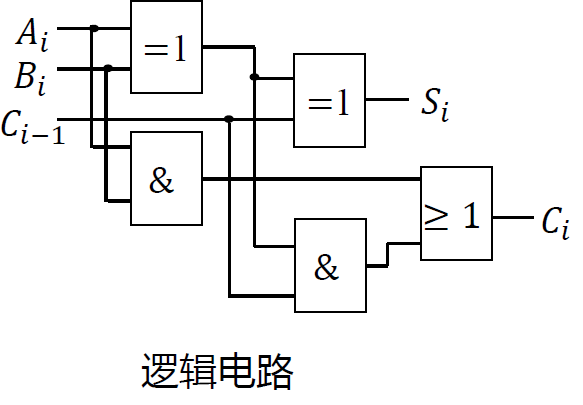
- 两个半加器的叠加
- $$ \begin{cases} S_i = A_i\oplus B_i \C_i = A_i B_i \end{cases} \Rightarrow \textcolor{#66ccff}{\begin{cases} S_i = A_i\oplus B_i\oplus C_{i_1} \ C_i = A_i B_i + (A_i\oplus B_i) C_{i-1} \end{cases}} $$
- 真值表 → 卡诺图 → 表达式
-
-
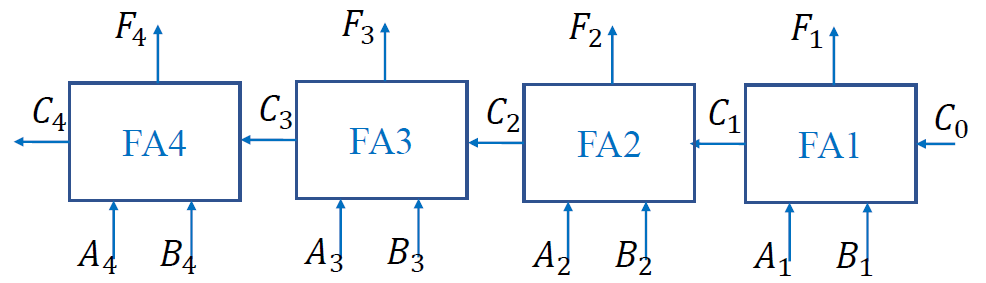
二进制并行加法器
- 串行进位二进制并行加法器
- 超前进位二进制并行加法器
-
串行进位二进制并行加法器
- 原理: 由数个全加器==级联== 构成, 高位的进位输入依赖于低位的进位输出
-
优点: 电路结构简单
缺点: 串行进位, 运算速度慢
-
关键: 多次进位浪费了时间
解决方案: 改串行进位为并行进位, 但 Si和 Ci由于依赖于 Ci-1,所以无法并行
-
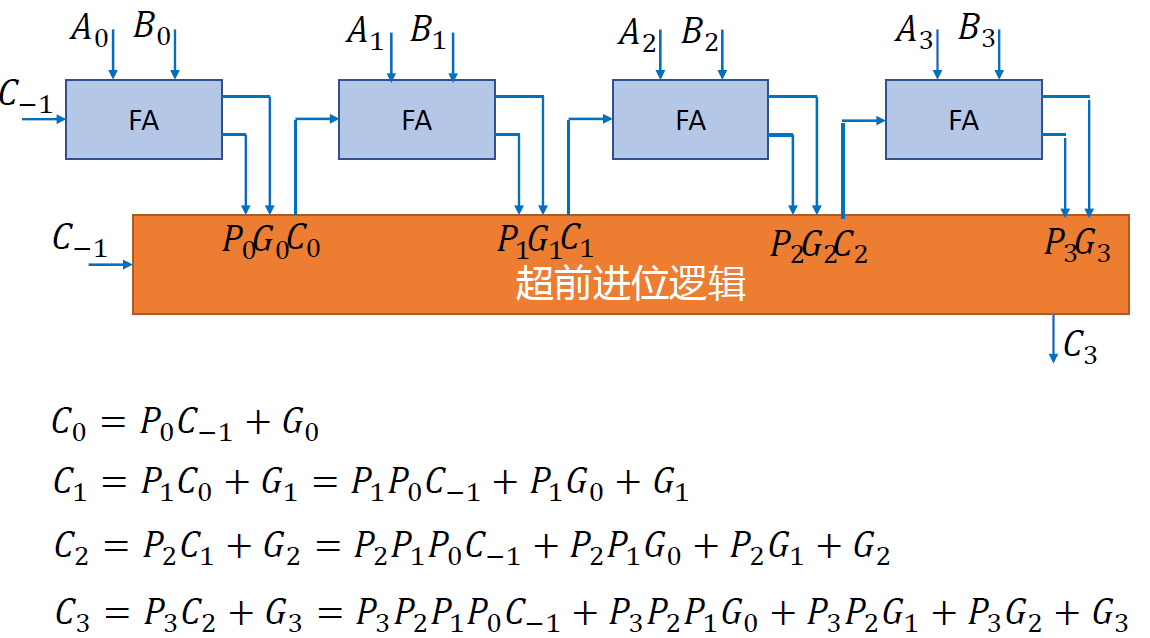
超前进位二进制并行加法器
- 原理: 根据输入信号同时形成各位向高位的进位,然后==同时产生各位的和== ; 也称为先行进位二进制并行加法器

- 四位超前进位并行加法器
78238逻辑符号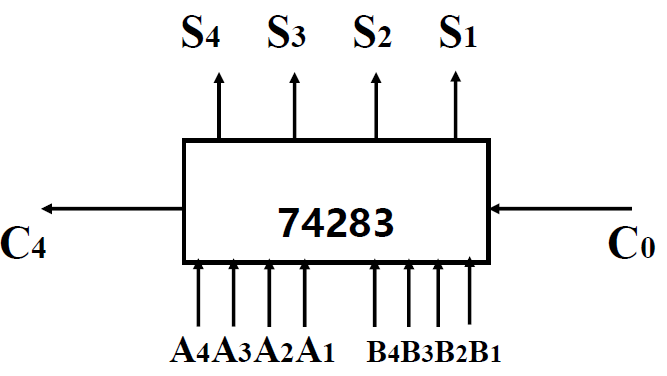
- 优点:运算速度快;缺点:电路结构较复杂 注意实际引脚顺序要看芯片引脚说明 P187
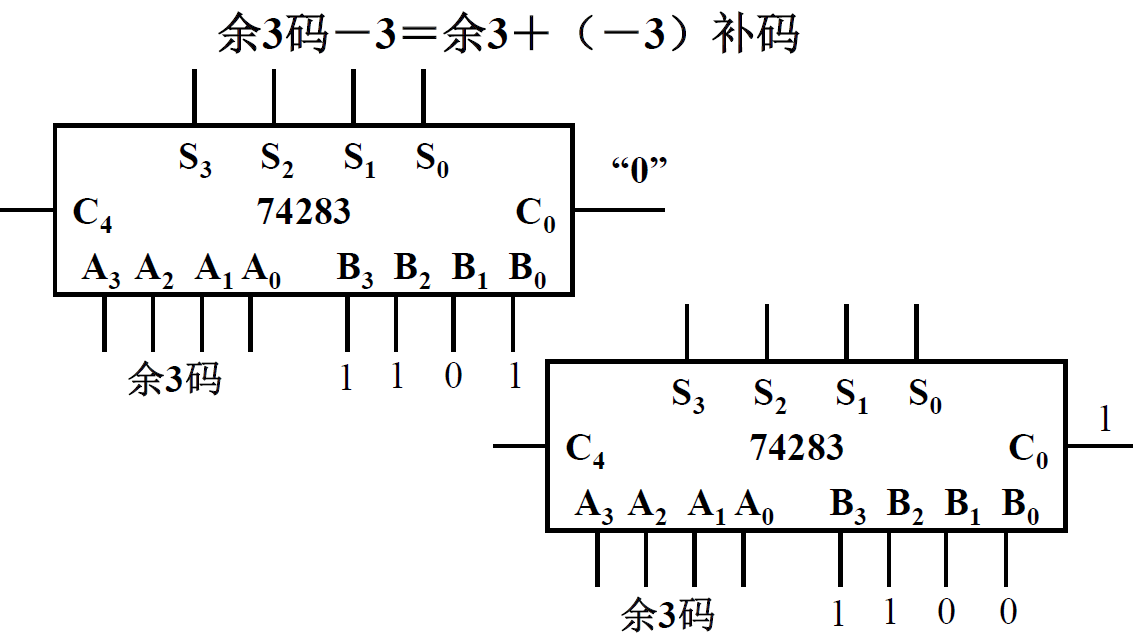
74283典型应用¶
-
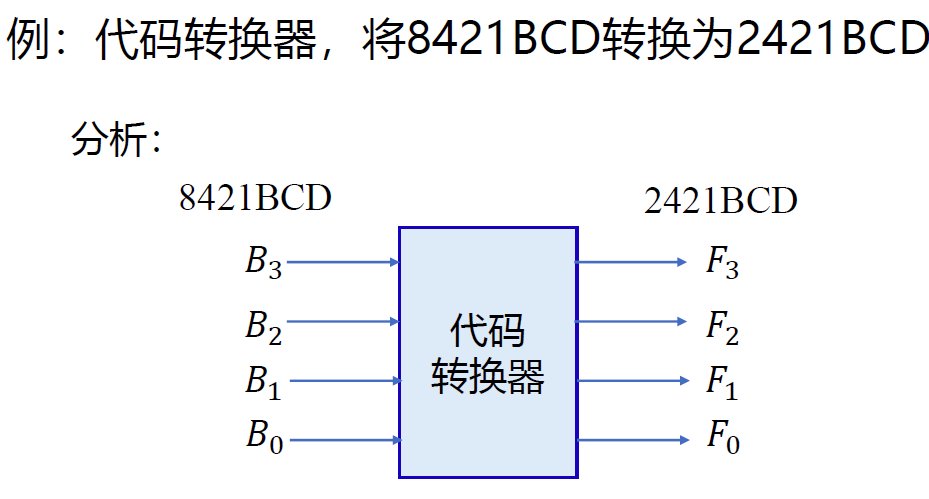
将 8421 码转换成余 3 码: \(一组输入为8421 一组输入为0011\)
-
将余 3 码转换成 8421 码:
- \(余3码-3\Rightarrow余3+(-3)补码\) -3 补码: 1101
-
上述两道综合,余 3 码和 8421 码相互转换
- \(加入控制信号M,M=0,8421→余3码;M=1,余3码→8421码\) B 处输入 0011 / 1101
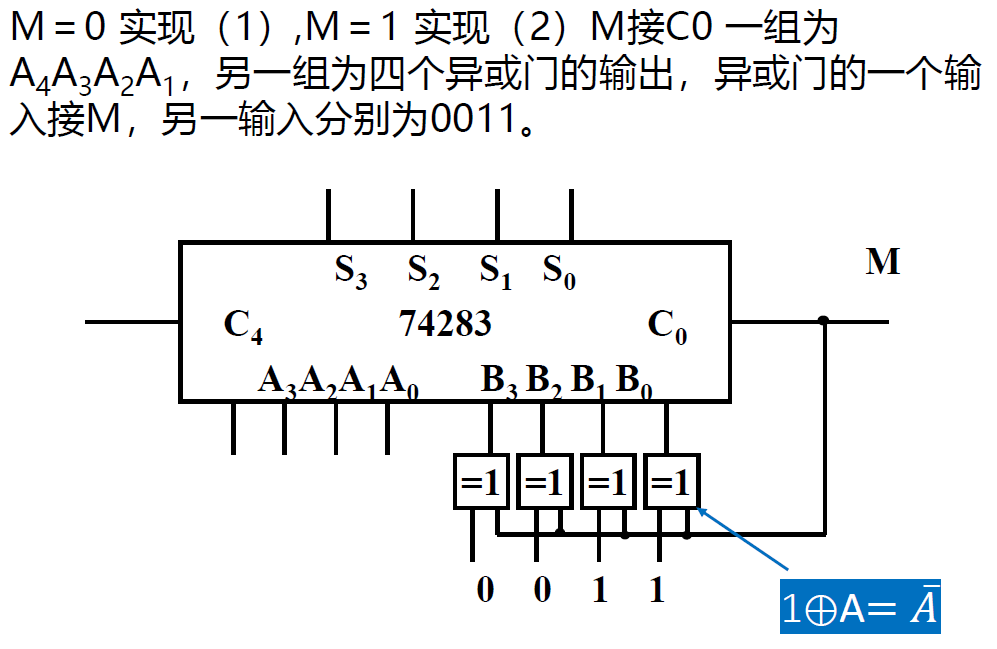
-
余三码加法运算
- 两个余 3 码的加法运算余 3 码相加要进行修正,即有进位时,加 3,无进位时,减 3。
- 使用两个 74283
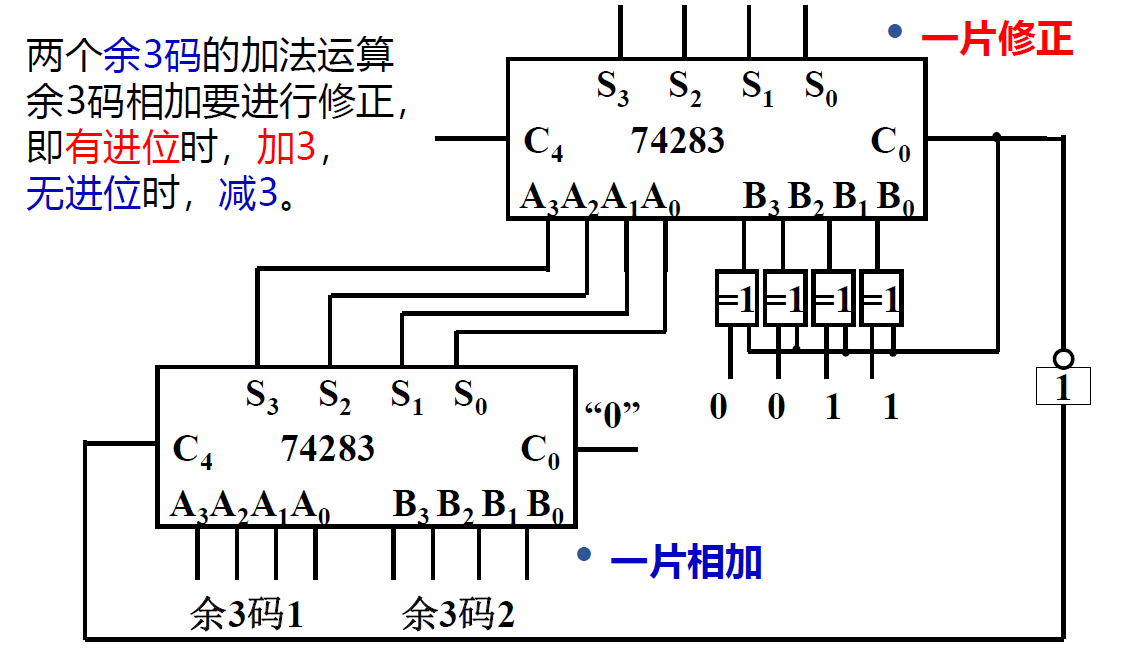
-
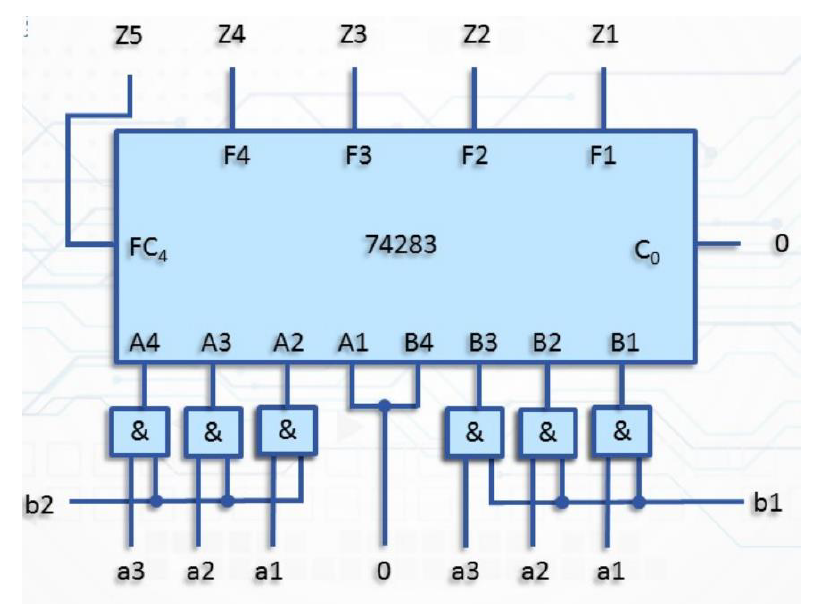
乘法运算: \(A×B, A=a_3a_2a_1(三位), B=b_2b_1(二位)\)
- 输入:A 的最大输入值为 111,B 的最大值为 11。𝐴 × 𝐵 的最大值为 10101
- 输出:\(Z_5Z_4Z_3Z_2Z_1\)
-
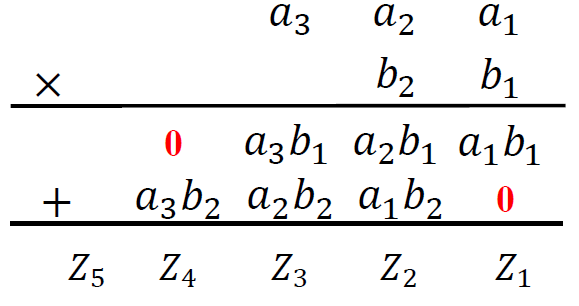
积(a1b1): 两输入与门 和(a2b1 + a1b2):两个四位二进制并行加法器
4.3.2 译码器¶
一. 变量译码器原理介绍 74139 74138¶
-
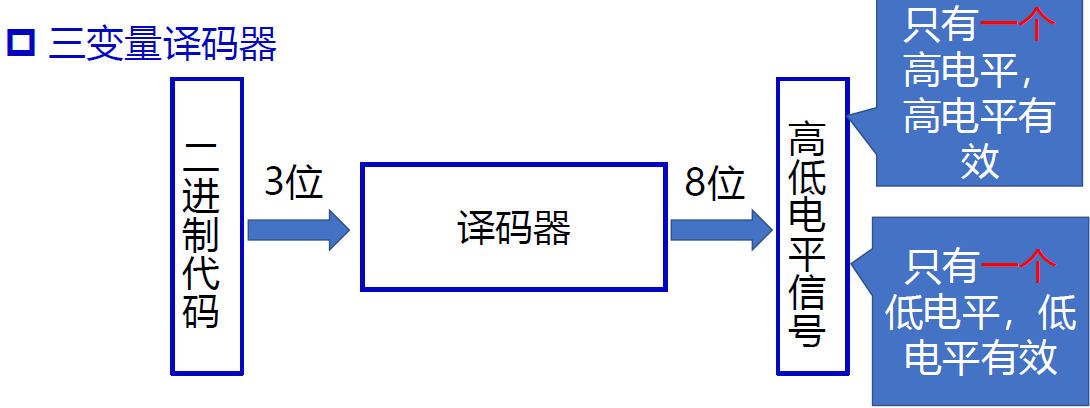
变量译码器----二进制译码器
-
特点
- 输入 n 个变量, 即 n 位代码
- 输出 2n 个, 即对应 n 个变量的 2n种组合,每个输出对应一种输入代码,即一个 𝑛 变量最小项
-
-
- 高电平输出有效二进制译码器,其输出逻辑表达式为:\(𝑌_𝑖 = 𝑚_𝑖\) (𝑚𝑖 为输入变量所对应的最小项)——“1”译中
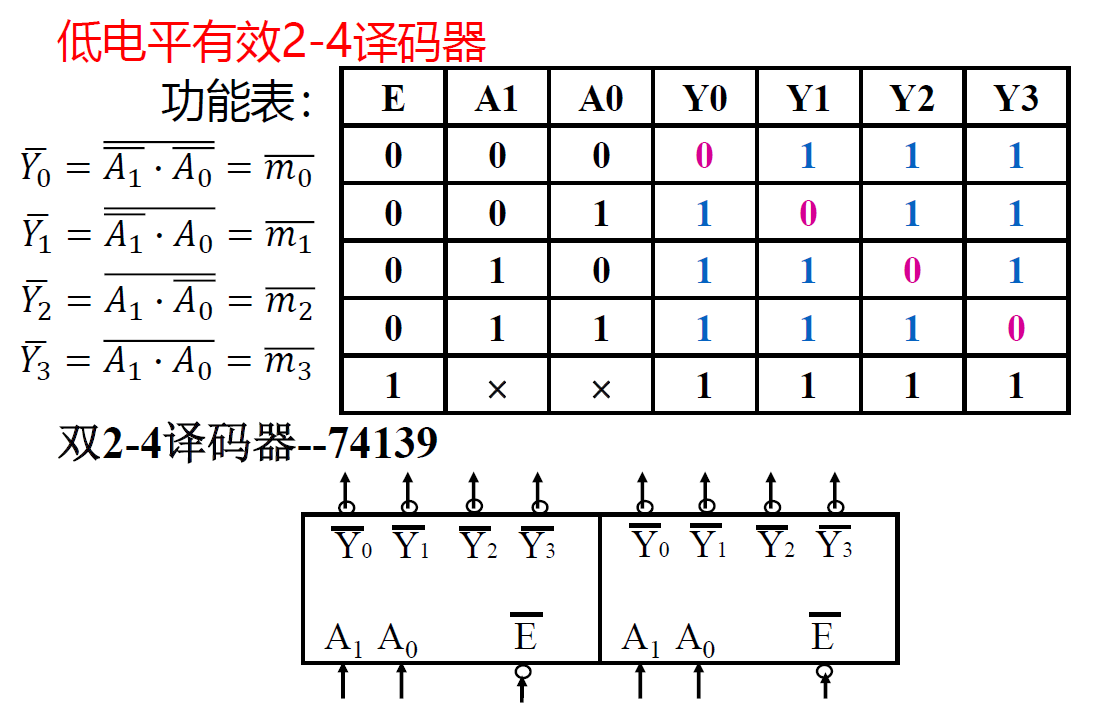
- 低电平输出有效二进制译码器,其输出逻辑表达式为:\(𝑌_𝑖 = \overline{𝑚_𝑖}\) (𝑚𝑖 为输入变量所对应的最小项)——“0”译中
- 课程中使用的都是低电平有效,即输出只有一个“0”,其他都为“1”
-
低电平有效 3-8 译码器
-
基本原理
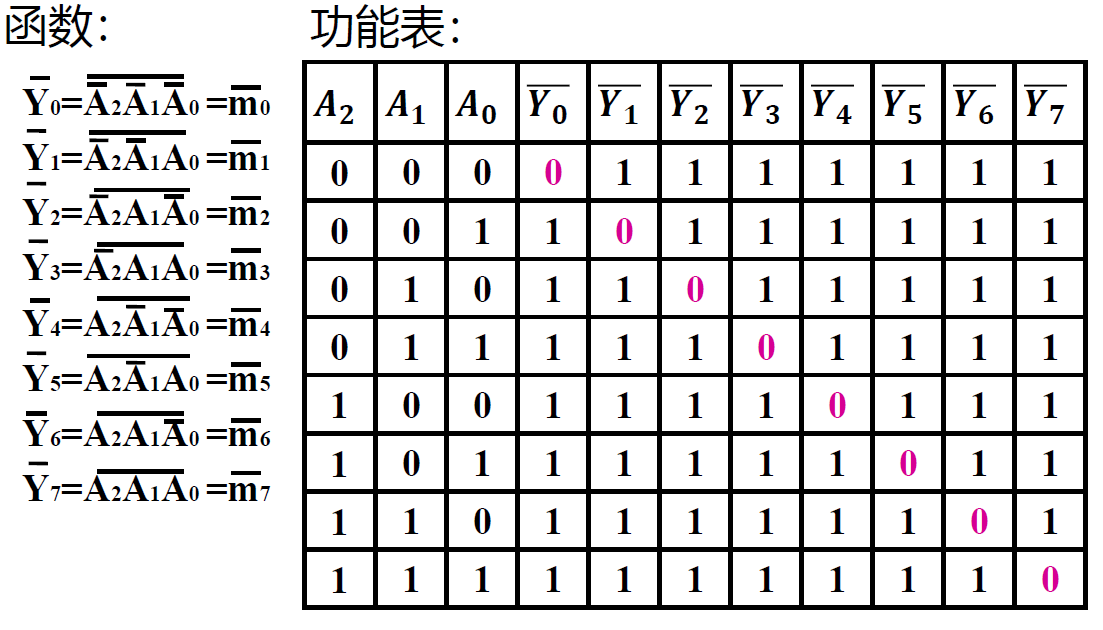
极小项(mi)是 0, 其余均为 1
-
3 线-8 线译码器—
74138- 图:
<img src="数字电路与逻辑设计.assets\image-20221008172143740.png" alt="image-20221008172143740" style="zoom:50%;" />- 三个输入,八个输出,输出低电平有效
- 三个使能输入端,只有当==\(S_1=1,𝑆_2 +𝑆_3 = 0\)== 时,译码器工作,否则译码器不工作 (可以控制使能输入端来进行选择)
-
二. 变量译码器典型应用¶
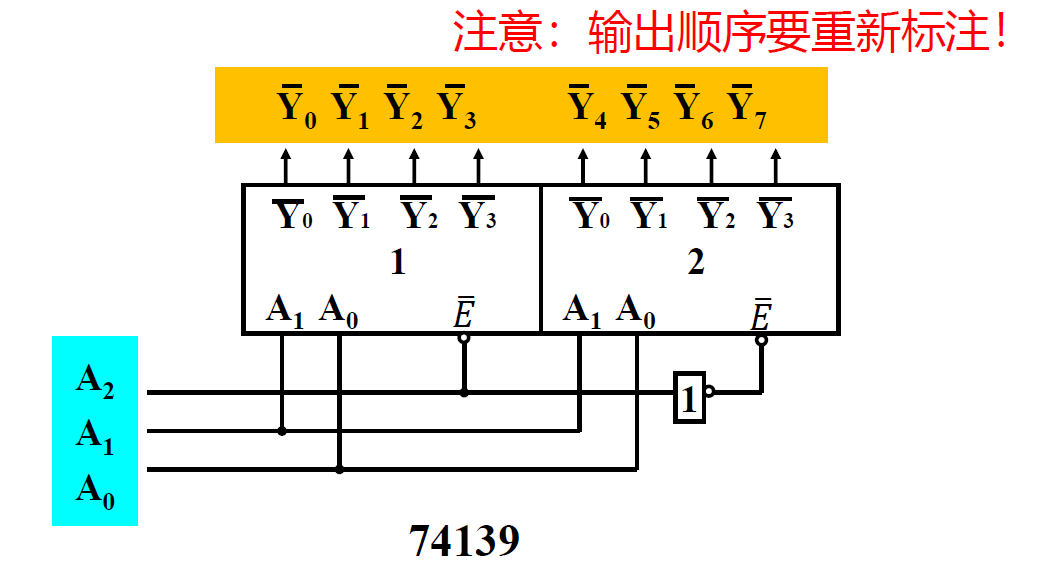
- 两个 2-4 译码器构成 3-8 译码器

- A2 的数值由输出的芯片是哪一片(即片选)决定
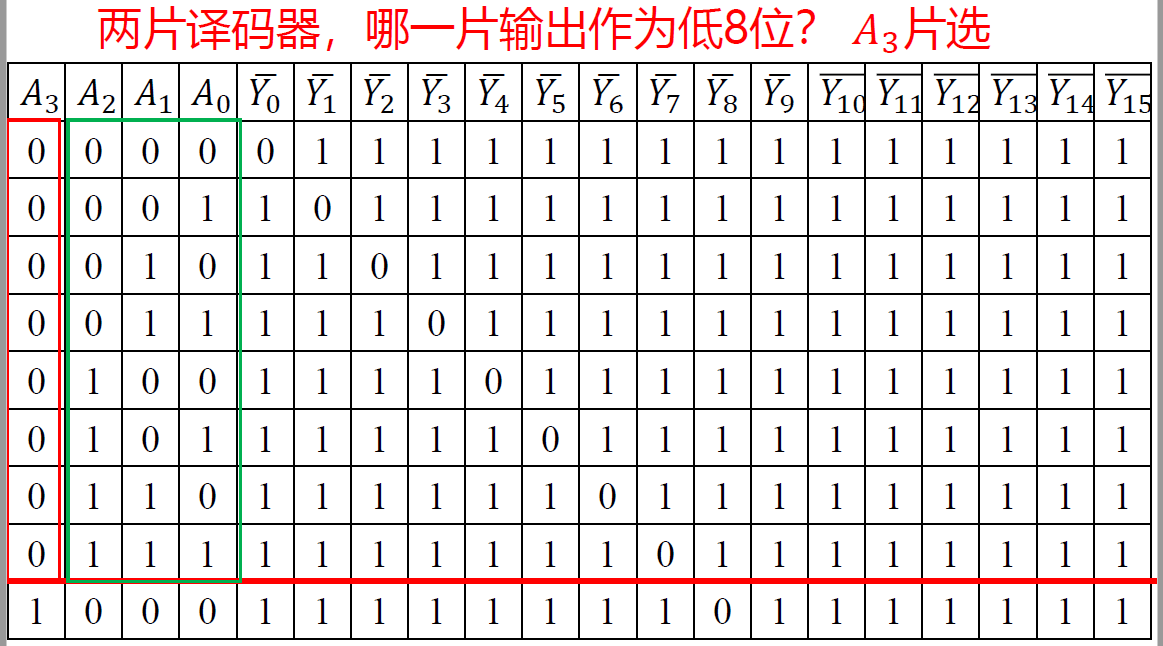
- 两个 3-8 译码器构成一个 4-16 译码器
- 与 ↑ 类似, 对 A3片选
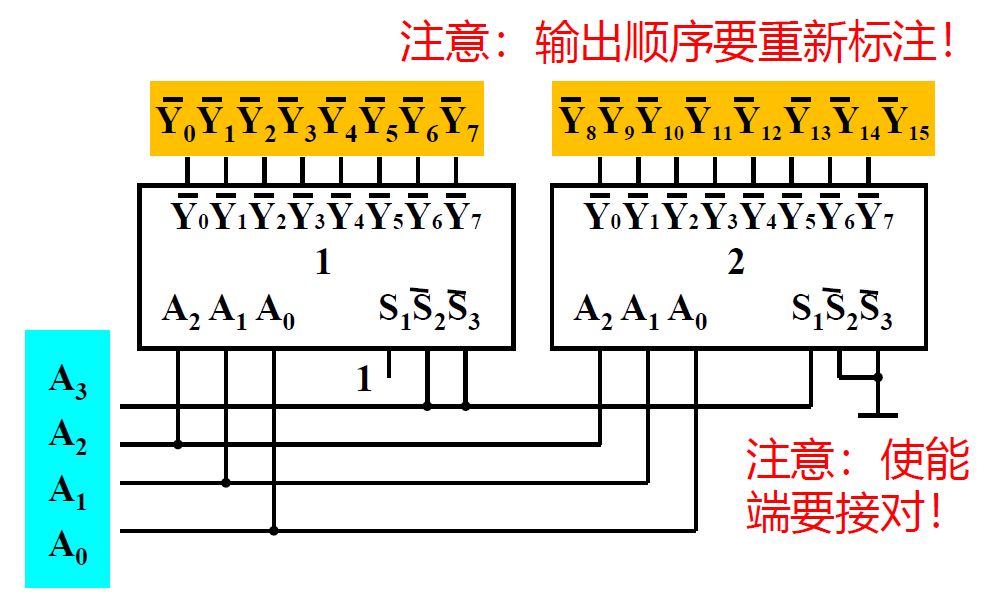
- 五片 2-4 译码器构成 4-16 译码器
- 简单的片选只能区分出一位数, 需要进行一次译码, 用译码结果进行片选
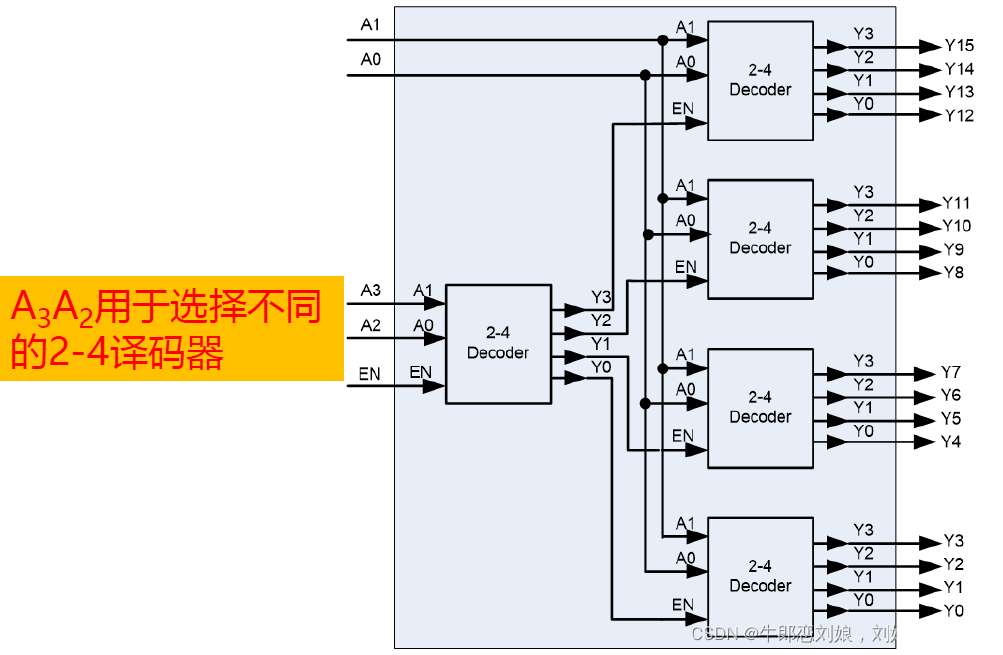
三. 芯片扩展-函数发生¶
-
任何函数都能够转化为最小项之和
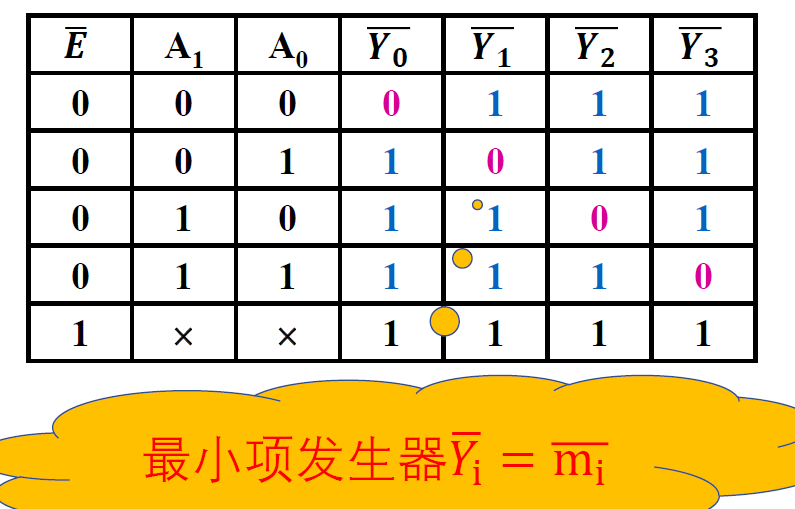
-
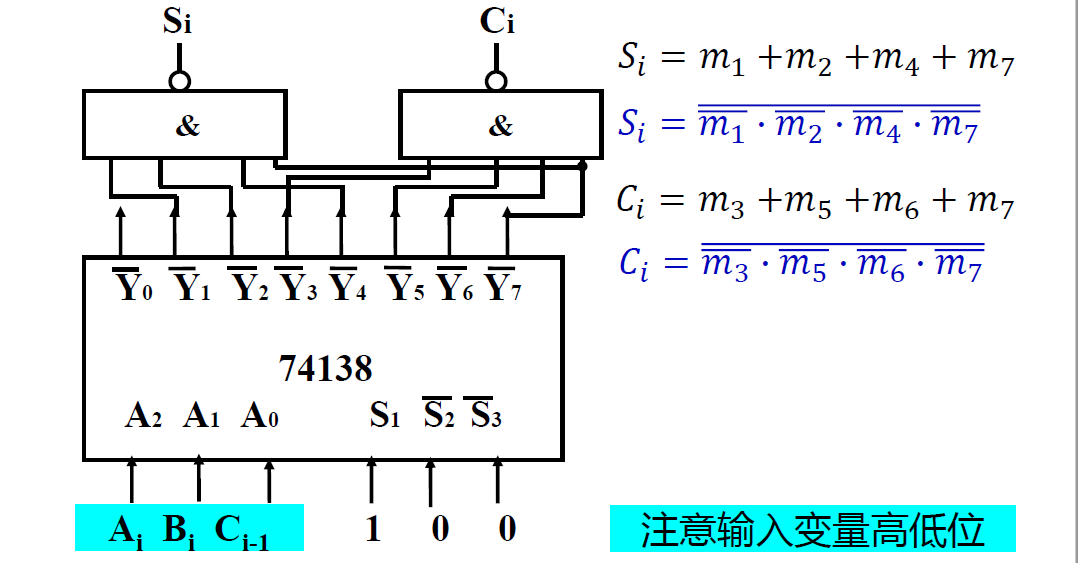
例----用 74138 构成一位全加器
-
\(S_i = \sum m^3(1,2,4,7)\quad C_i = \sum m^3(3,5,6,7)\)
\(S_i = m_1+m_2+m_4+m_7 = \overline{\overline{m_1} \cdot\overline{m_2} \cdot\overline{m_4}\cdot\overline{m_7}}\)
\(C_i = m_3+m_5+m_6+m_7 = \overline{\overline{m_3} \cdot\overline{m_5} \cdot\overline{m_6}\cdot\overline{m_7}}\)
-
-
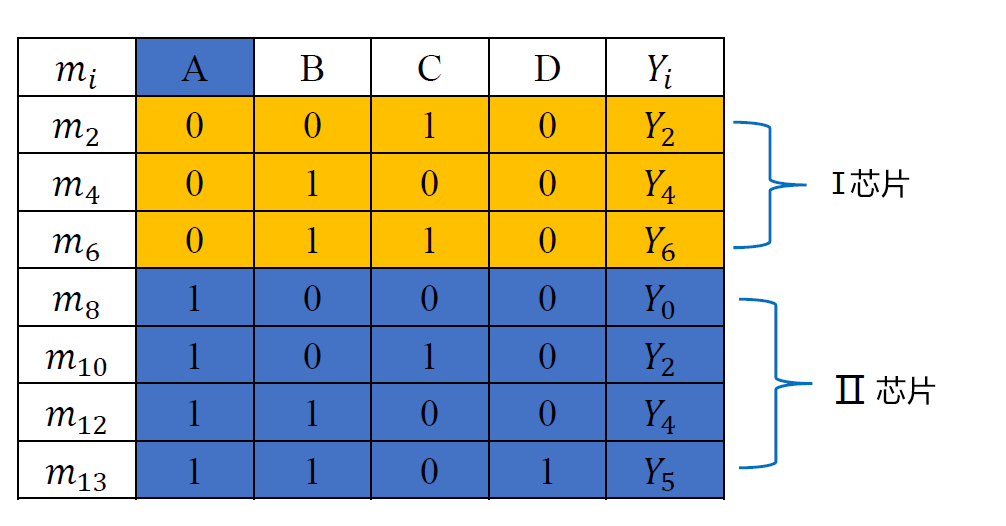
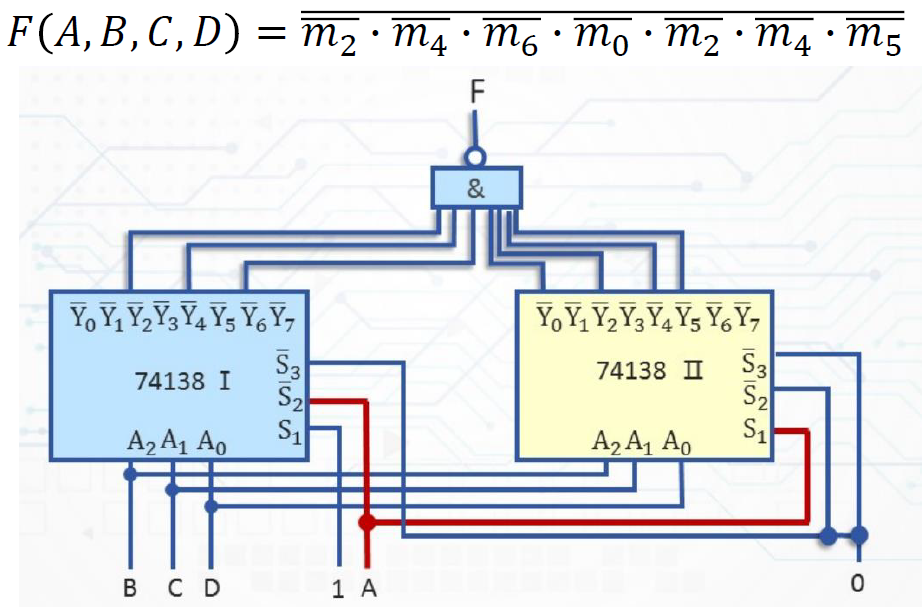
例----用 74138 和与非门实现逻辑函数 \(F(A,B,C,D)=\sum(2,4,6,8,10,12,13)\)
-
分析
- 逻辑函数有四个变量
- 将两个 3-8 译码器扩展成 4-16 译码器
- 用译码器的一个使能端作为变量的输入端
-
-
例----用 74138 和与非门实现逻辑函数 \(F(A,B,C,D)=\sum(2,4,6,8,10,12,14)\)
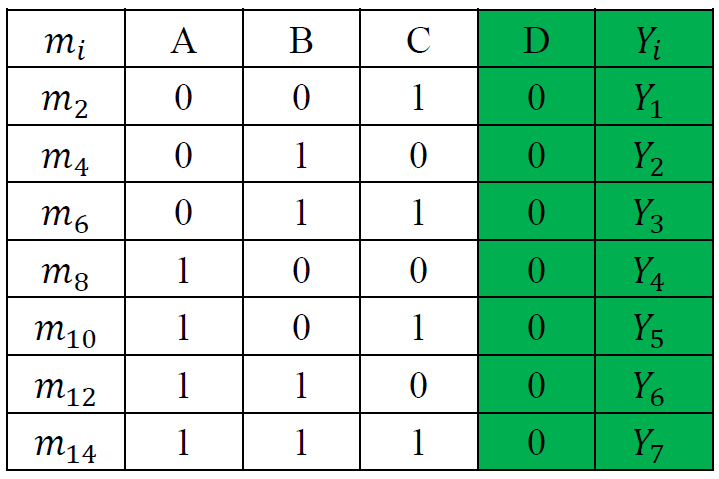
- D 全部为 0, 只需要一个 3-8 译码器就能解决
-
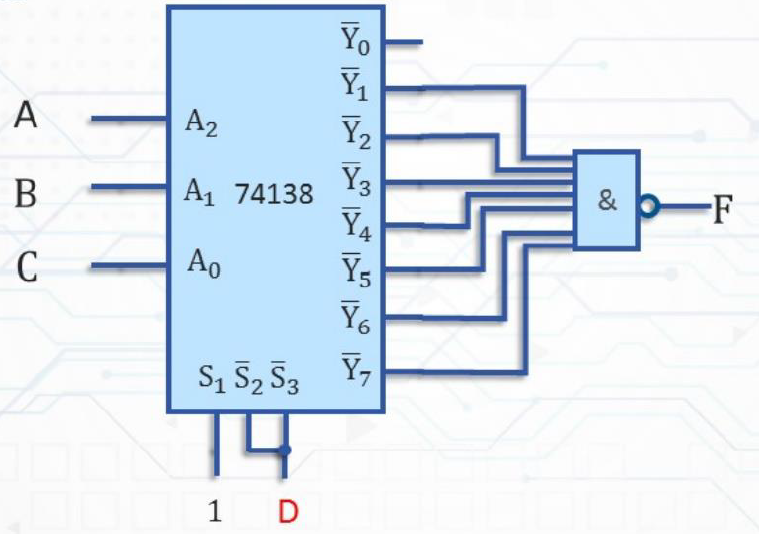
例----用
74138和与非门实现逻辑函数 \(F(A,B,C)=AC+BC\)- \(F(A, B, C) = AC+BC = \overline{A}BC + A\overline{B}C + ABC\)
- \(F(A, B, C) = \sum m(3, 5, 7) = \overline{m_0}\cdot\overline{m_1}\cdot\overline{m_2}\cdot\overline{m_4}\cdot\overline{m_6}\)
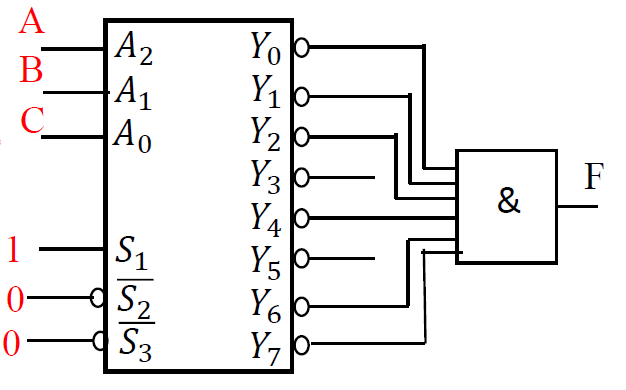
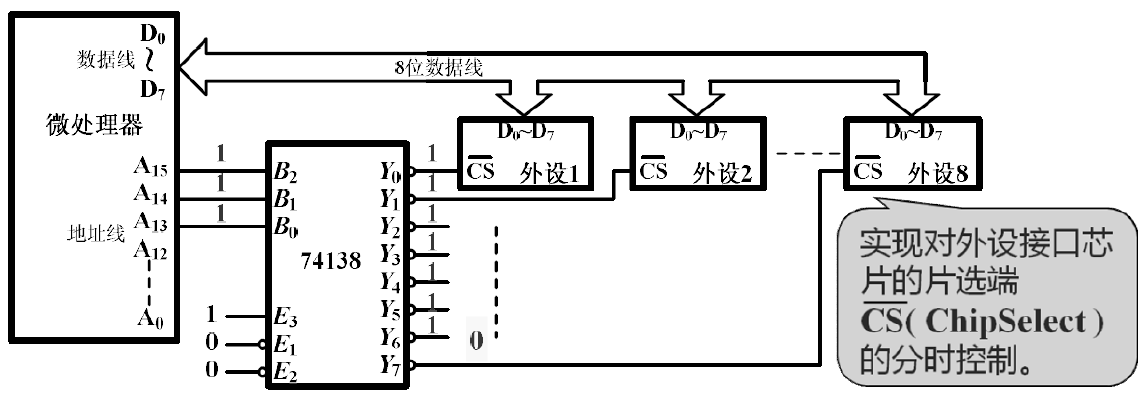
四. 译码器实际应用¶
地址译码----用于标识外围设备和存储单元的地址, 确定外设的寻址范围
4.3.3 选择器¶
一. 数据选择器原理介绍¶
-
引入:
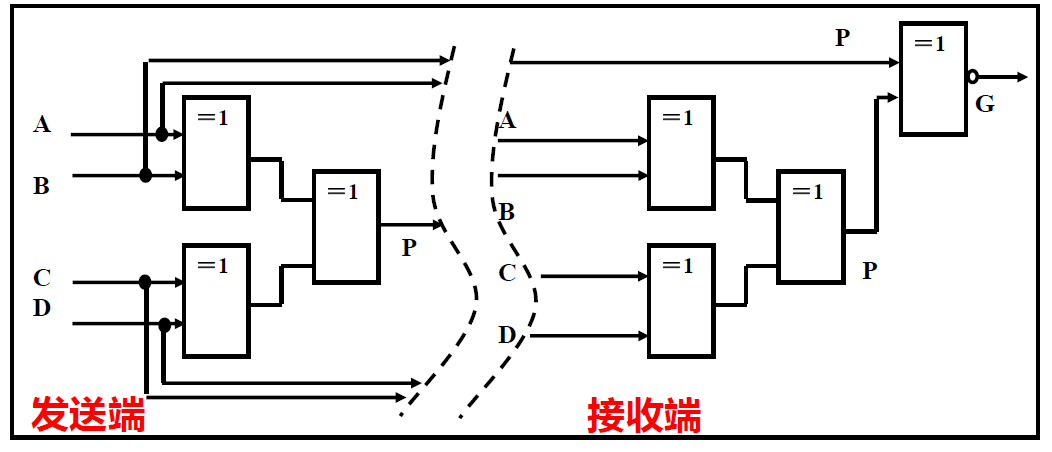
- 在数字电路中,当需要进行远距离多路数据传输时,为了减少传输线的数目,发送端常通过一条公共传输线,用多路选择器分时发送数据到接收端,接收端利用多路分配器分时将数据分配给各路接收端,其原理如图所示。

-
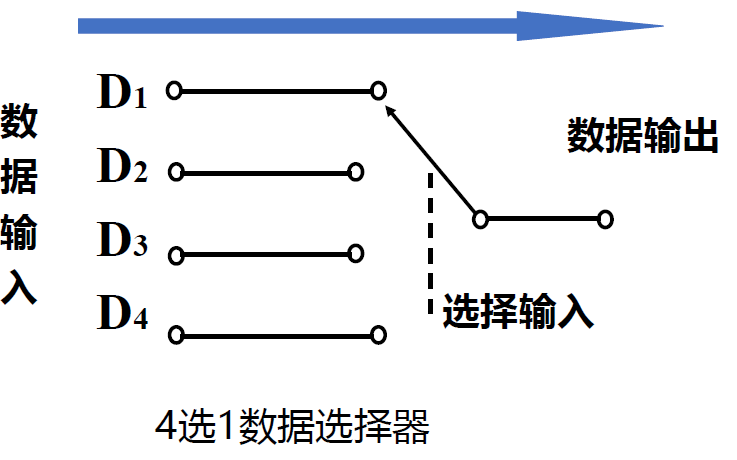
数据选择器(Multiplexer -MUX)
- 从多路数据中选择其中所需要的一路数据传送到输出端的电路,也称 多路选择器 或 多路开关
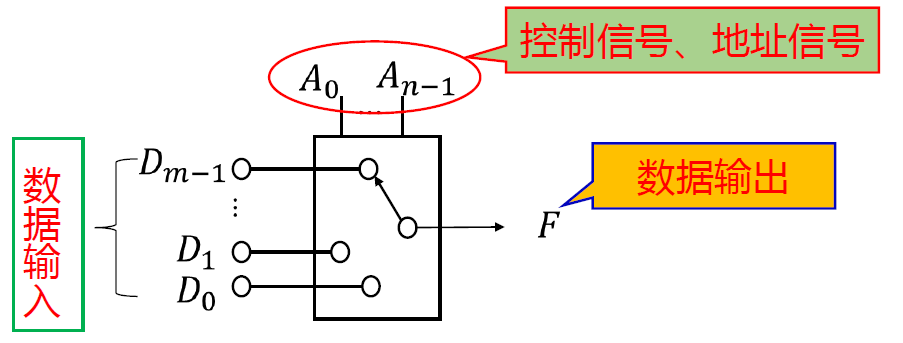
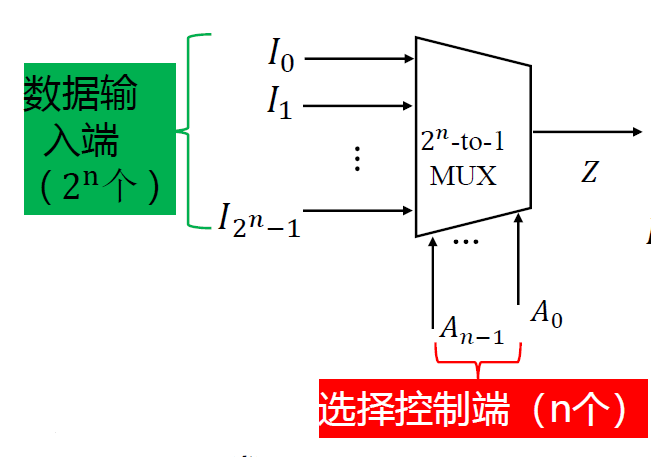
- n 位地址变量/控制信号(An-1...A0), 有 2n路数据通道, 实现 2n选 1 功能
-
 \(\Rightarrow\)
\(\Rightarrow\) 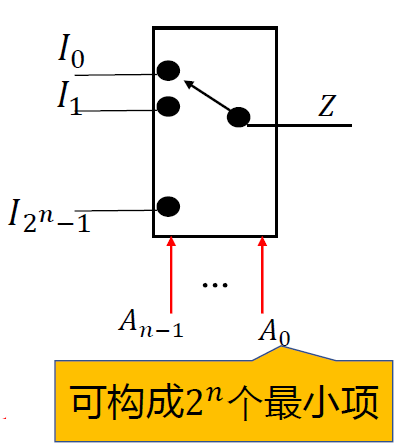
-
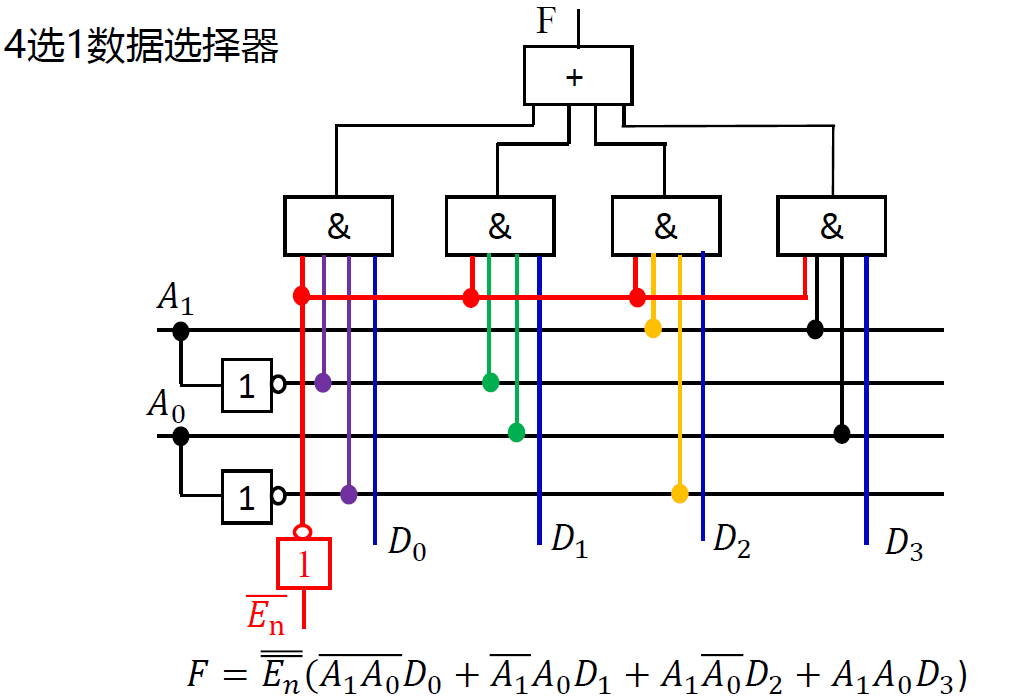
\(Z = \sum_{k=0}^{2^n - 1} m_k I_k\)
-
mk : n 个控制变量(An-1...A0)的最小项; Ik : 第 k 路数据输入
第 k 个最小项 mk 控制 第 k 路数据输出 Ik
-
-
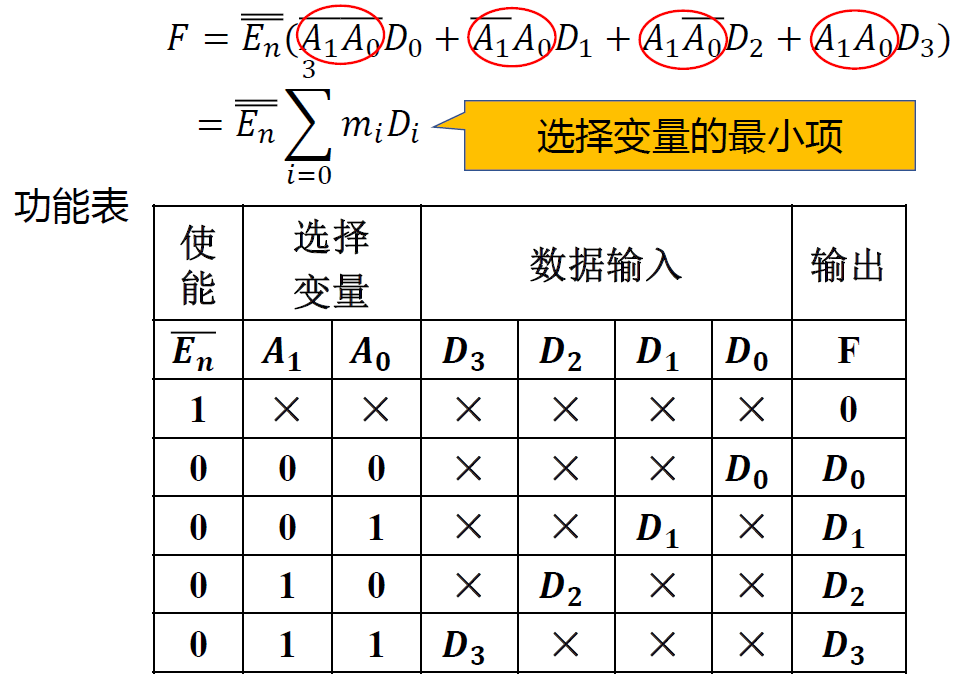
4 选 1 数据选择器 ---- 74153¶
-
逻辑符号 引脚图 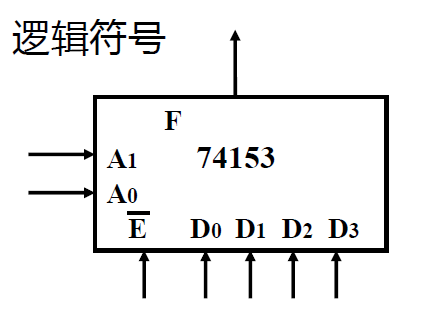
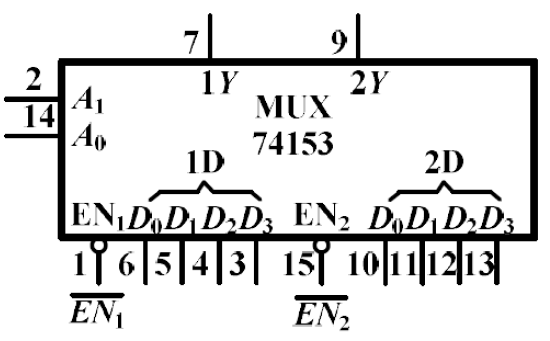
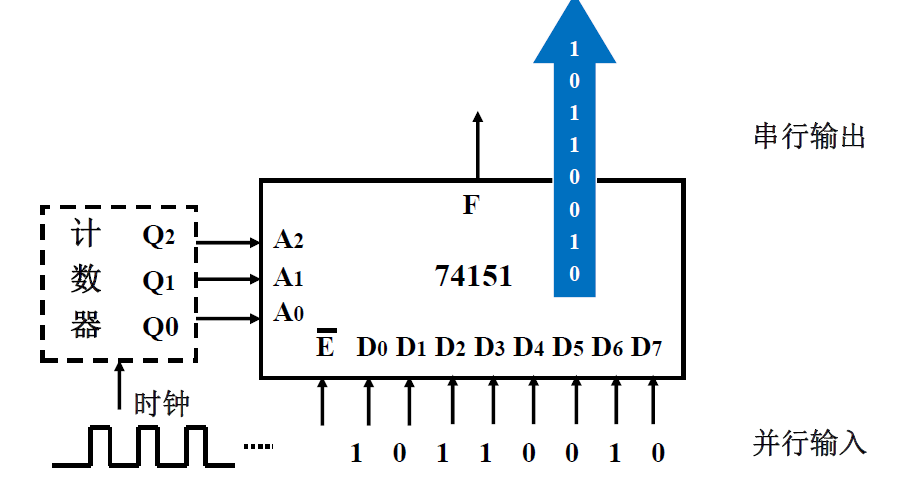
中规模 8 选 1 数据选择器74151. 74251¶
74251: 三态输出,使能端输入高电平,则输出==高阻态==
-
逻辑符号 引脚图 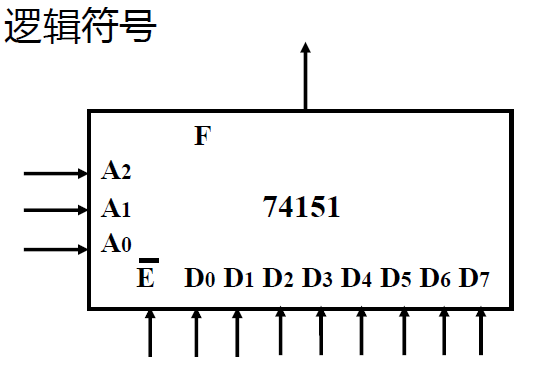
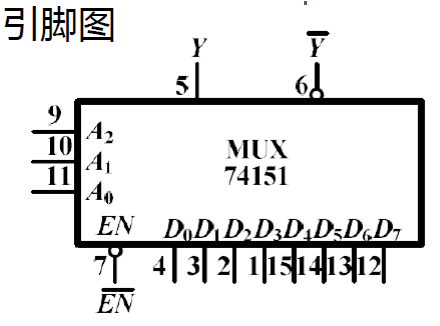
二. 数据选择器典型应用¶
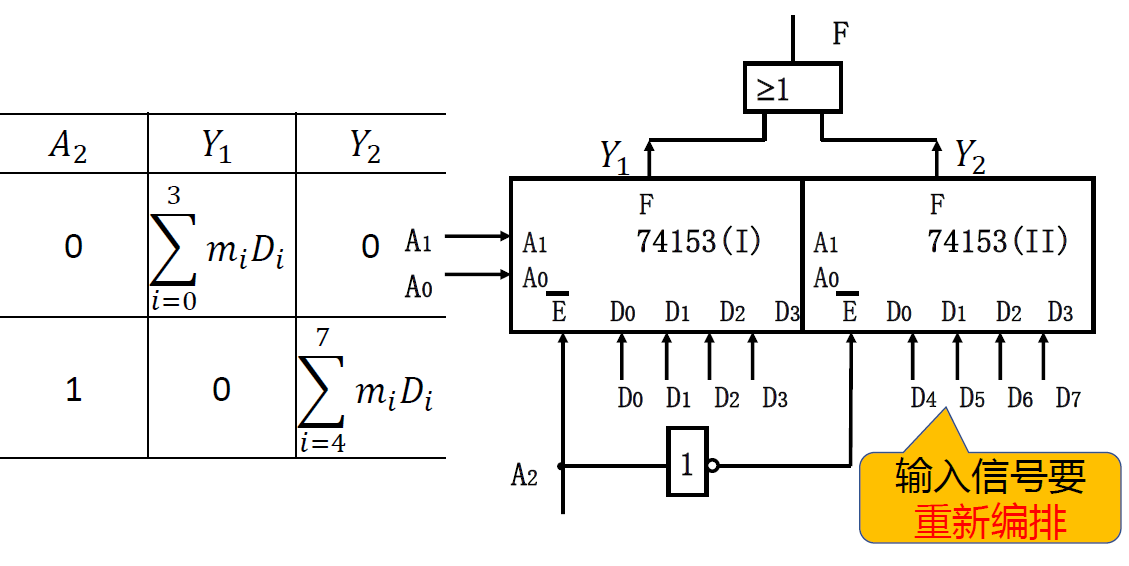
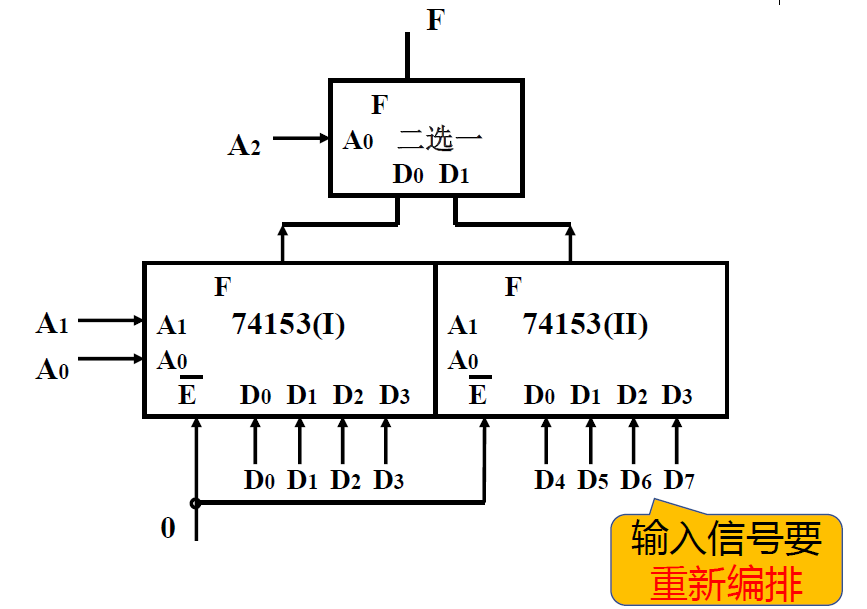
芯片扩展¶
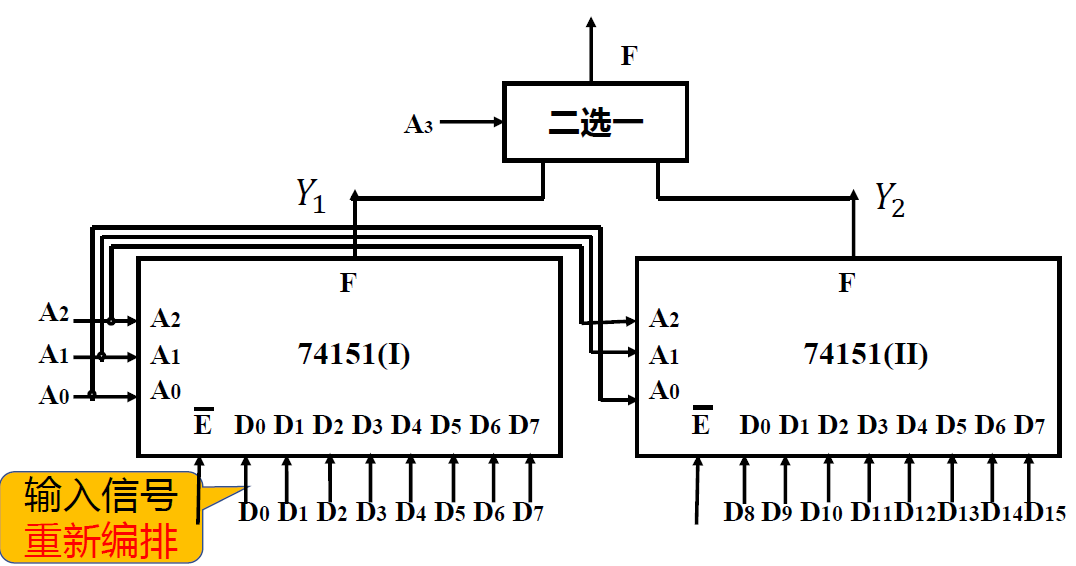
- 用两个 4 选 1 构成一个 8 选 1
- 法一: 使用使能端. 输出接或门; A2 的正
- 负作为使能信号
- 法二: 不使用使能端. 接 2 选 1 选择器, A2 作为选择信号
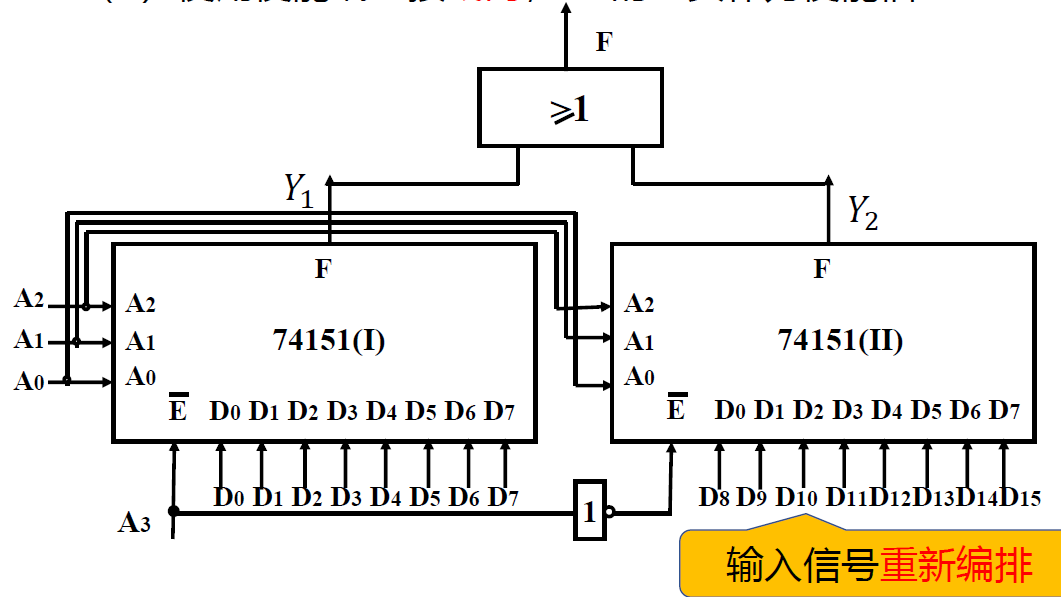
- 用 2 个 8 选 1 构成一个 16 选 1
- 法一: 使用使能端. 输出接或门; A3 的正负作为使能信号
- 法二: 不使用使能端. 接 2 选 1 选择器, A3 作为选择信号
- 法一: 使用使能端. 输出接或门; A3 的正负作为使能信号
函数发生¶
-
由数据选择器的一般式可知,以 8 选 1 公式 \(𝐹=\sum^7_{i=0}𝑚_𝑖 𝐷_𝑖\) 为例,给不同的 𝐷𝑖 赋予 0 或 1 的取值就可以选取不同的最小项,从而实现任意组合逻辑函数的产生。
-
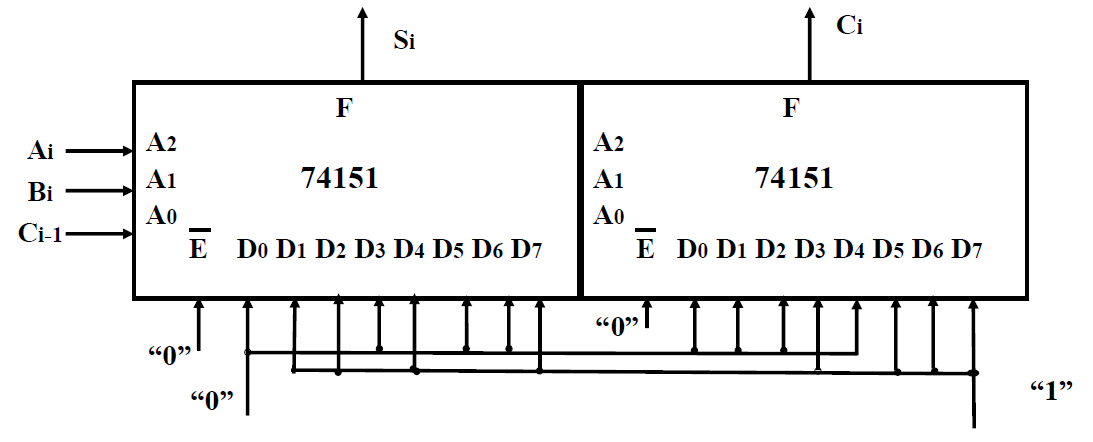
例: 用 8 选 1 数据选择器实现全加器
- \(S_i = \sum m^3(1,2,4,7)\quad \Rightarrow \begin{cases} D_1=D_2=D_4=D_7=0\\ D_0=D_3=D_5=D_6=1 \end{cases}\)
- \(C_i = \sum m^3(3,5,6,7) \Rightarrow \begin{cases} D_3=D_5=D_6=D_7=0\\ D_0=D_1=D_2=D_4=1 \end{cases}\)
-
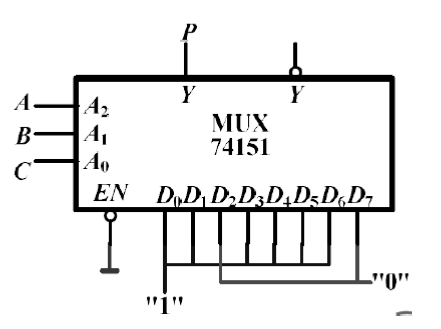
用 8 选 1 选择器实现函数 \(P=A\overline{C} + \overline{A}C + \overline{B}\)
- 法一: 代数法
-
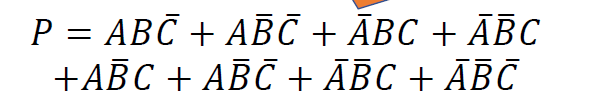 - \(P(ABC) = \sum m(0, 1, 3,4, 5, 6) \Rightarrow\)
- \(P(ABC) = \sum m(0, 1, 3,4, 5, 6) \Rightarrow\) 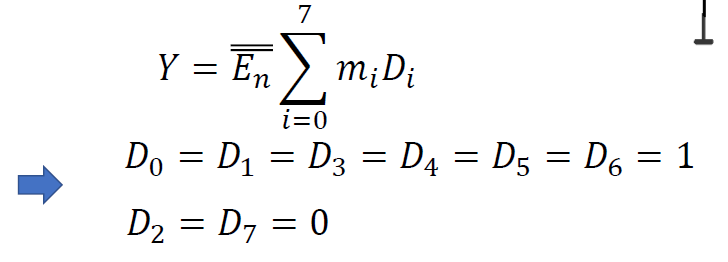 -
- 
- 法二: 卡诺图法
-
 - 之后同样化为极小项之和(主析取范式), 选择取 1/0 的 Di
- 之后同样化为极小项之和(主析取范式), 选择取 1/0 的 Di
- 法一: 代数法
-
-
用==4 选 1 选择器== 实现函数 \(F(A, B, C, D) = \sum m^4(1,2,4,9,10,11,12,14,15)\)
- 设数据选择器的地址==A1A0 = AB== , 用==数据输入端== 来实现 C 和 D
-
卡诺图化简法 代数化简法 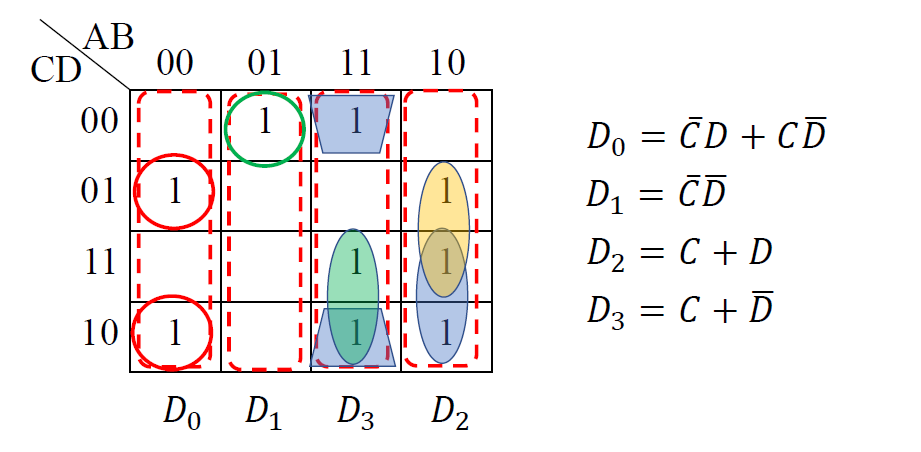

- 逻辑电路图:
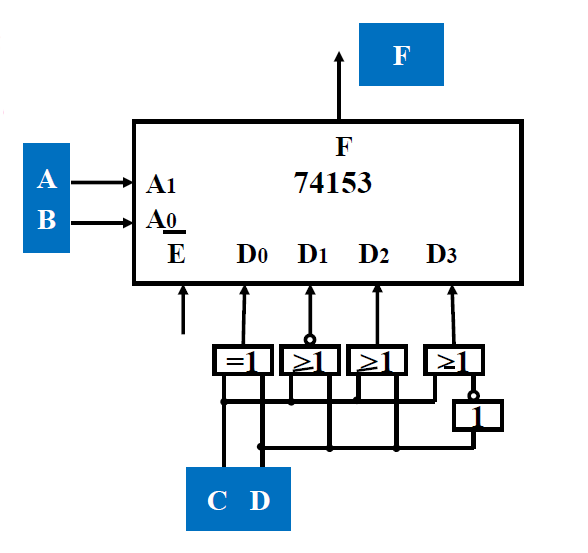
并行转串行¶
- 8 选一, 3 个地址输入端由模 8 计数器控制,整个电路实现8 路的并行输入到1 路输出的串行转换过程
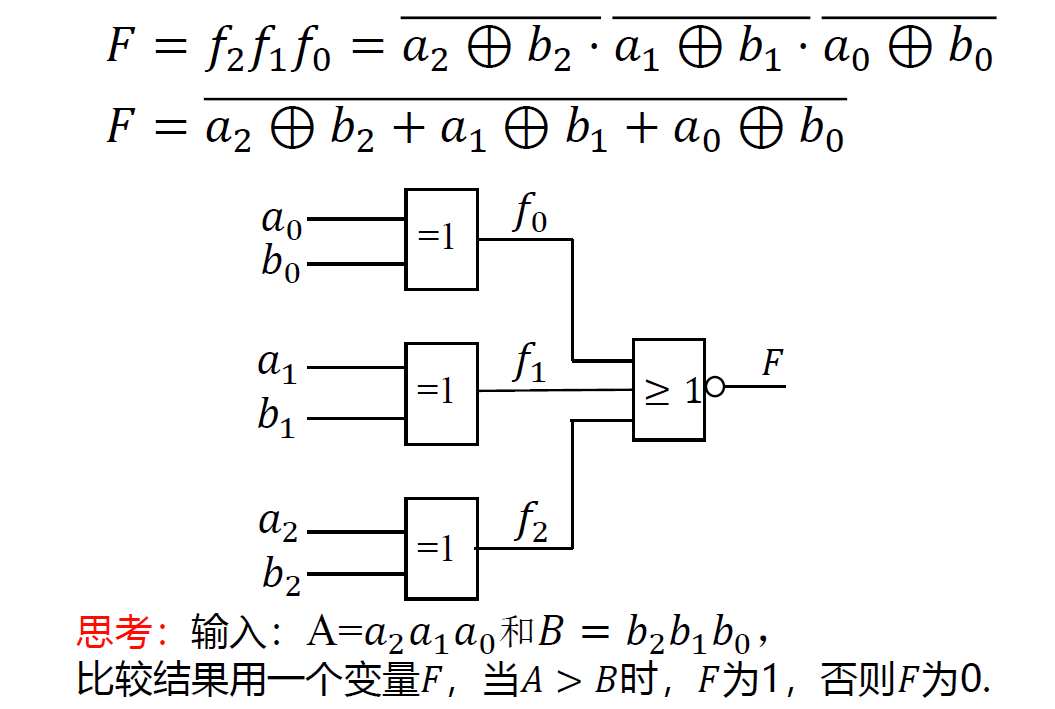
4.3.4 数码比较器[略]¶
-
作用: 用来判断两个二进制数的大小或者相等
-
一位数值比较器 真值表
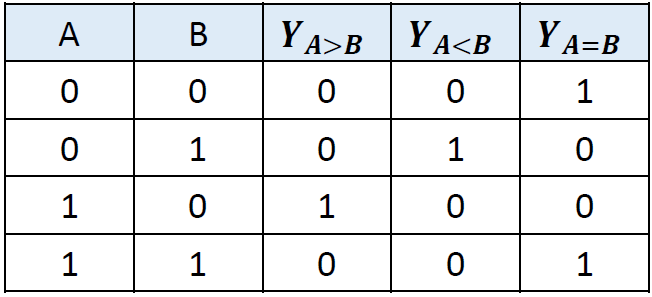
-
表达式
- \(Y_{A>B} = A\overline{B}\)
- \(Y_{A<B} = \overline{A}B\)
- \(Y_{A=B} = A\odot B\)
-
逻辑图
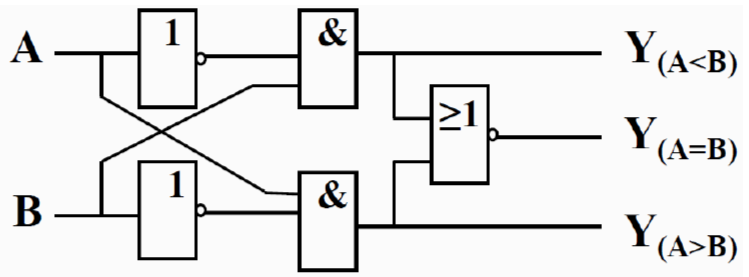
-
多位比较
- 比较两个多位数,应首先从高位开始,逐位比较。跟写算法题一样 XD
-
例:\(𝐴=𝐴_3𝐴_2𝐴_1𝐴_0;\ 𝐵=𝐵_3𝐵_2𝐵_1𝐵_0\)
-
① 首先比较 𝐴3和 𝐵3,如果 𝐀𝟑𝐁𝟑=𝟏𝟎,则 𝑨>𝑩 如果 𝐀𝟑𝐁𝟑=𝟎𝟏,则 𝑨<𝑩 如果 𝐀𝟑𝐁𝟑=𝟎𝟎 或 𝟏𝟏,则 比较 𝐴2和 𝐵2 ② 比较 𝐴2和 𝐵2,如果 𝐀𝟐𝐁𝟐=𝟏𝟎,则 𝑨>𝑩 如果 𝐀𝟐𝐁𝟐=𝟎𝟏,则 𝑨<𝑩 如果 𝐀𝟐𝐁𝟐=𝟎𝟎 或 𝟏𝟏,则 比较 𝐴1和 𝐵1
③ 比较 𝐴1和 𝐵1,如果 𝐀𝟏𝐁𝟏=𝟏𝟎,则 𝑨>𝑩 如果 𝐀𝟏𝐁𝟏=𝟎𝟏,则 𝑨<𝑩
如果 𝐀𝟏𝐁𝟏=𝟎𝟎 或 𝟏𝟏,则 比较 𝐴0和 𝐵0
④ 比较 𝐴0和 𝐵0,如果 𝐀𝟎𝐁𝟎=𝟏𝟎,则 𝑨>𝑩 如果 𝐀𝟎𝐁𝟎=𝟎𝟏,则 𝑨<𝑩 如果 𝐀𝟎𝐁𝟎=𝟎𝟎 或 𝟏𝟏,则 𝑨=𝑩
-
四位大小比较器
7485逻辑符号 引脚图 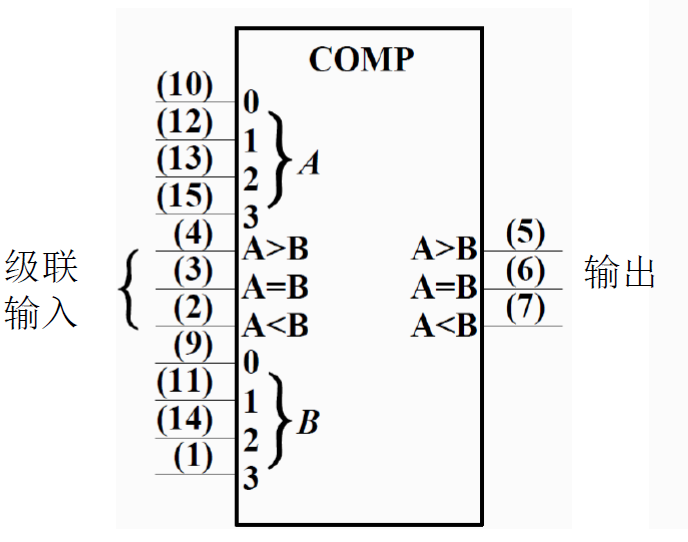
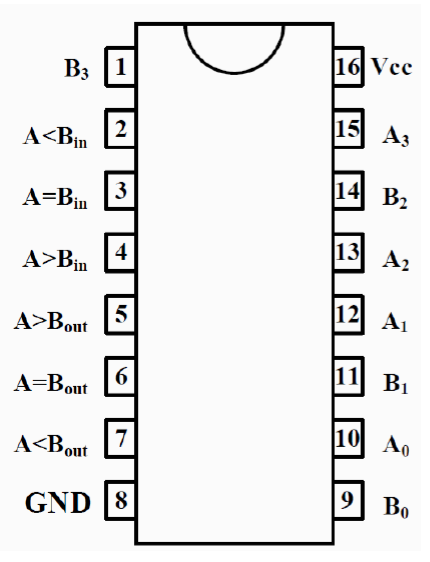
-
真值表
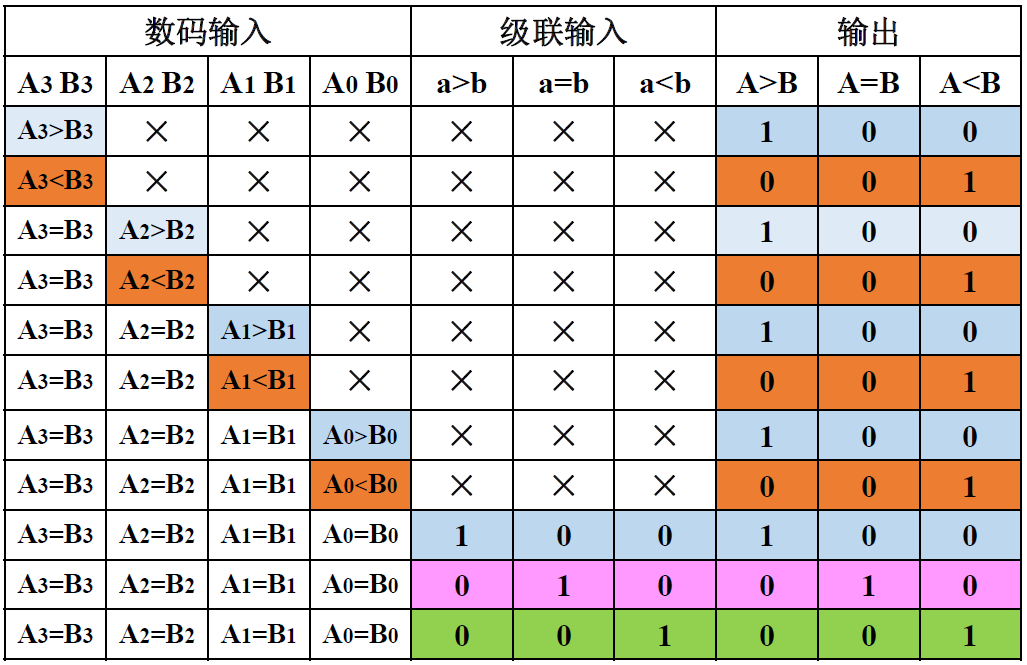
-
-
拓展应用
-
四位比较拓展为八位比较器
- 串行比较: 用两块
7485串联, 把低一级的的7485输出接高一级的级联输入端,低7485的级联输入端接 010 。 -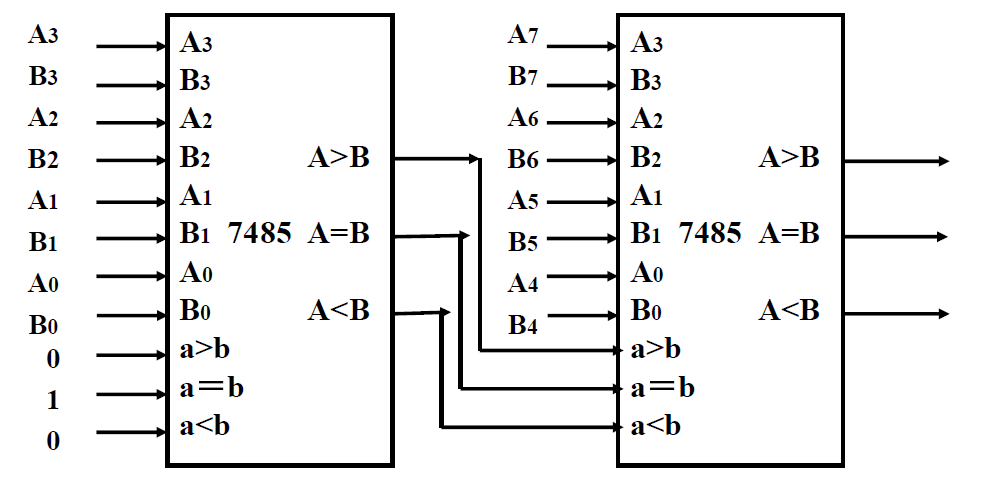
-
十六位数值比较器(并行接法)
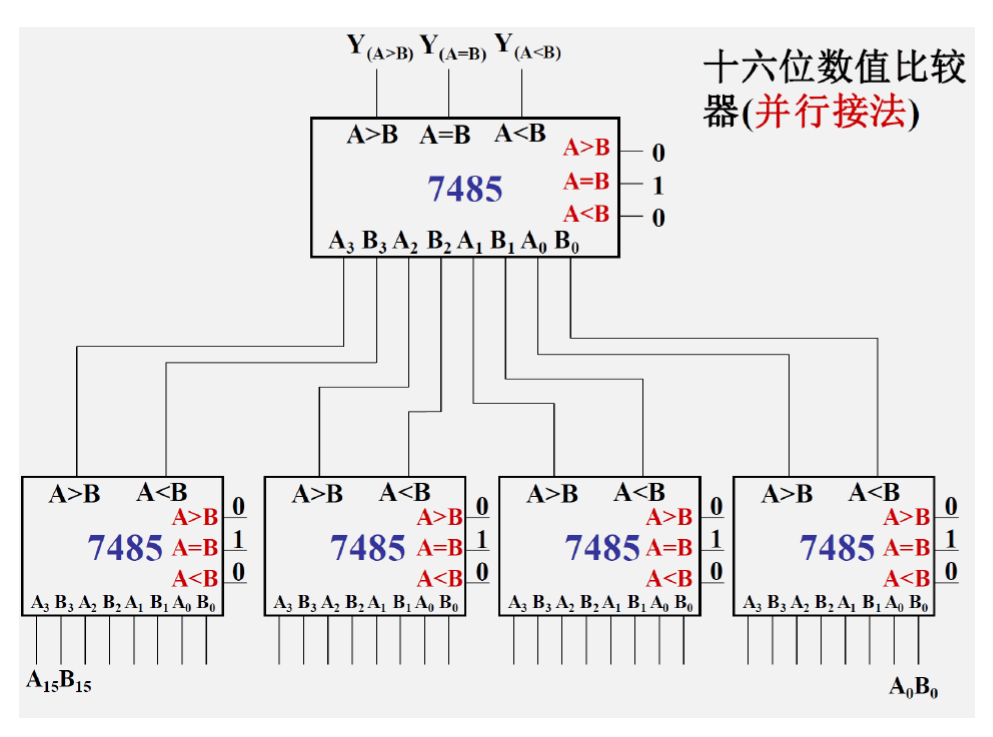
-
4.3.5 奇偶校验电路[略]¶
-
作用: 用来检查数据传输和存取过程中是否产生错误的组合逻辑电路。(就是检测数据中包含"1"的个数是奇数还是偶数)
-
应用: 广泛应用于计算机的内存储器以及磁盘等外部设备中。
-
奇偶校验发生器:可产生奇偶校验位,与数据一起传输或保存 奇偶校验检测器:可检验所接受的数据和奇偶校验位
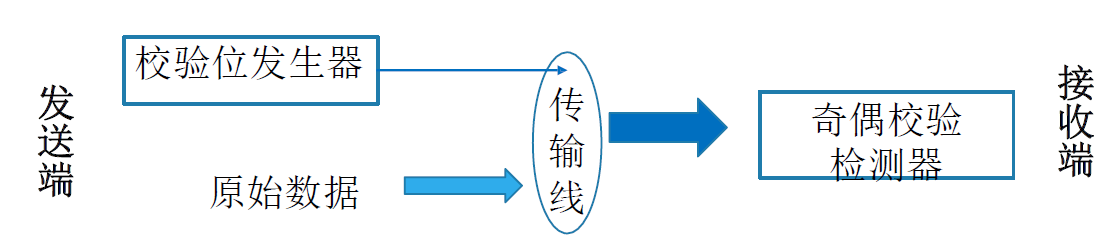
-
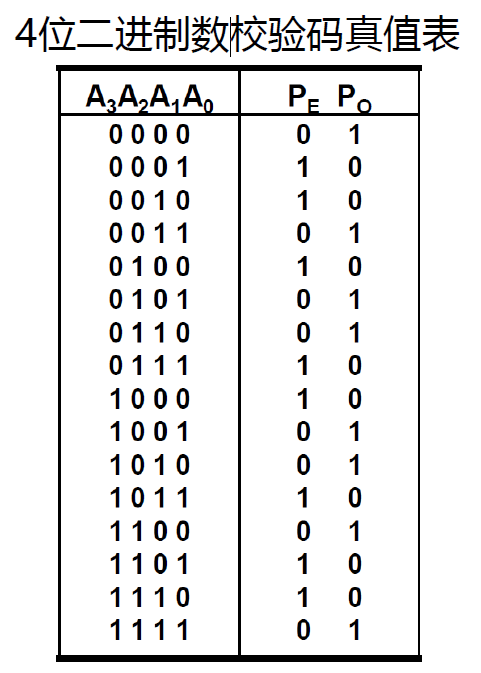
被校验的n 位原始数据和1位校验位组成 n+1 位校验码。
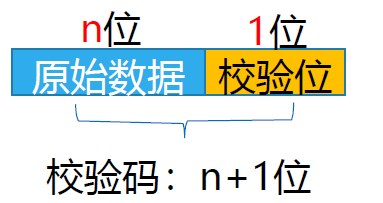
-
如何进行校验
- 采用奇偶校验码时,对收到的代码,可通过检查含“1”个数的奇偶来判断是否有错。
- 例如,当采用偶检验时,若收到的代码中含奇数个“1”则说明发生错误。
第五章 时序逻辑电路¶
总述¶
-
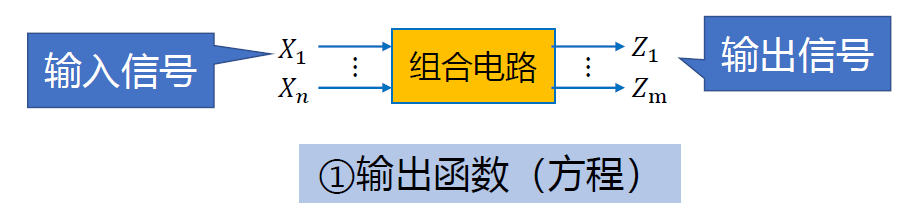
组合逻辑电路
- 电路的输出: 仅与==当前时刻的输入== 有关 𝑍𝑚=𝑓𝑚(𝑥1,𝑥2,⋯,𝑥𝑚)
- 逻辑函数唯一: 只有一组 𝑍𝑚=𝑓𝑚(𝑥1,𝑥2,⋯,𝑥𝑚)
- 电路框图:
-
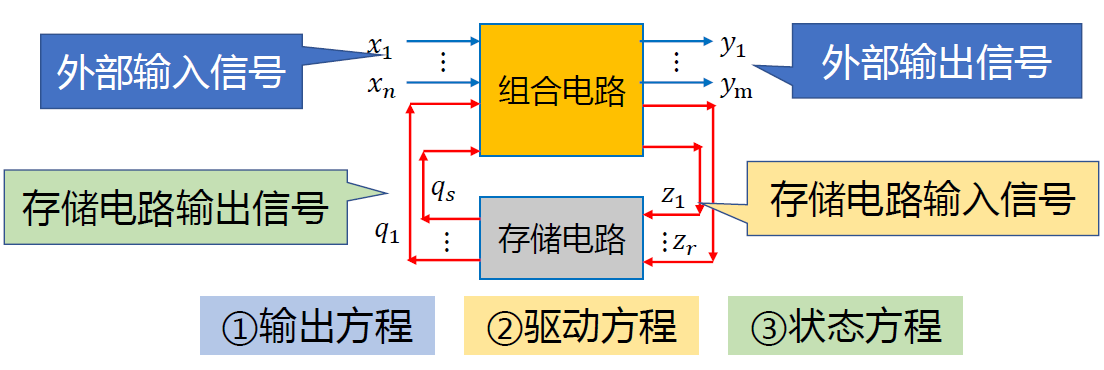
时序逻辑电路
-
电路的输出与以下均有关:
- 当前时刻的输入 𝑥𝑖
- 电路过去(上一个时刻)的工作状态 y𝑚=𝑓𝑚(𝑥1,⋯,𝑥𝑚, 𝑞1,⋯,𝑞𝑠 )
-
电路框图:
-
三大方程组描述逻辑关系

-
用向量形式表示\(\begin{cases}Y = F(X, Q^n)\\Z = G(X, Q^n)\\Q^{n+1} = H(Z, Q^n)\end{cases}\)
- 一个时序逻辑电路可以用这 3 个方程清楚的描述出来, 此三大方程为今后分析和设计时序逻辑电路的关键
-
注意:
- 现态(原态):存储电路当前时刻的状态 𝑄𝑛 - 次态(新态):存储电路下一时刻的状态 𝑄𝑛+1
-
5.1 触发器¶
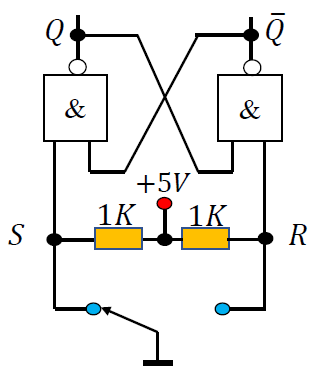
5.1.1 基本 RS 触发器¶
-
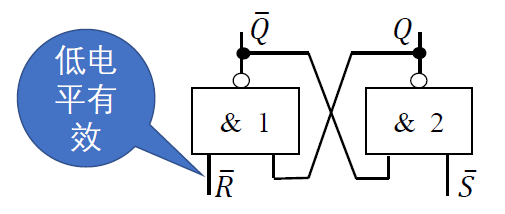
基本 RS 触发器,又称RS 锁存器,是各种触发器电路中结构最简单的一种,是各种复杂电路结构触发器的基本组成部分。
-
电路结构: 由两个与非门首尾相接,交叉耦合构成。
- 有两个触发输入端\(\overline{R} 和 \overline{S}\)
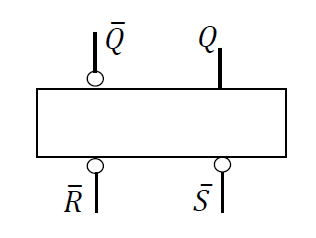
- \(Q^n : 现态\quad Q^{n+1}: 次态\)
-
𝑅:置 0 端 (Reset the Q=0 清零端, 复位端)
𝑆:置 1 端 (Set the Q=1 置位端)
- 有两个触发输入端\(\overline{R} 和 \overline{S}\)
-
工作原理
-
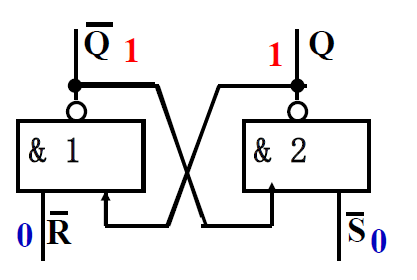
输入\(\overline{R} = \overline{S} = 1\textcolor{orange}{(R=S=0)}\) 时, 保持原态
- 若原状态: \(Q = 1, \overline{Q} = 0\) 输出: \(Q = 1, \overline{Q} = 0\) 保持原态 -
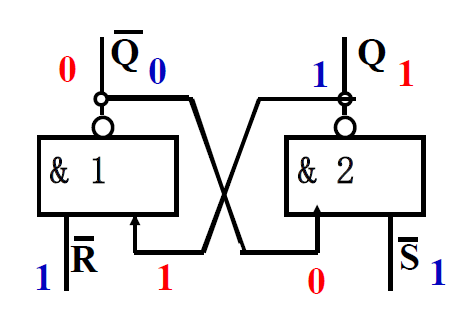 - 若原状态: \(Q = 0, \overline{Q} = 1\) 输出: \(Q = 0, \overline{Q} = 1\) 保持原态
-
- 若原状态: \(Q = 0, \overline{Q} = 1\) 输出: \(Q = 0, \overline{Q} = 1\) 保持原态
- 
-
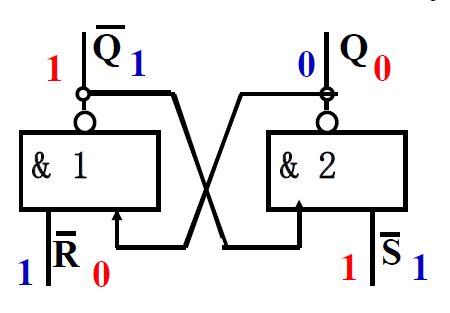
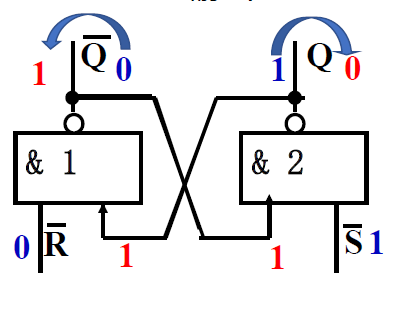
输入\(\overline{R} = 0, \overline{S} = 1 \textcolor{orange}{(R=1)}\)时, 触发器为 0 态, \(Q=0, \overline{Q} = 1\)
- 若原状态: \(Q = 0, \overline{Q} = 1\) 输出: \(Q = 0, \overline{Q} = 1\) 保持原态 -
 - 若原状态: \(Q = 1, \overline{Q} = 0\) 输出: \(Q = 0, \overline{Q} = 1\) 清 0
-
- 若原状态: \(Q = 1, \overline{Q} = 0\) 输出: \(Q = 0, \overline{Q} = 1\) 清 0
- 
-
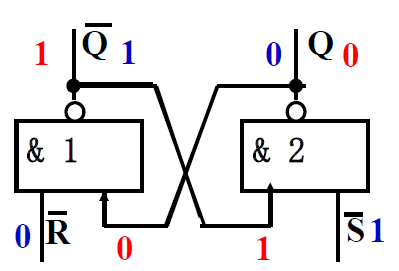
输入\(\overline{R} = 1, \overline{S} = 0 \textcolor{orange}{(S=1)}\)时, 触发器为 1 态, \(Q=1, \overline{Q} = 0\)
- 若原状态: \(Q = 1, \overline{Q} = 0\) 输出: \(Q = 1, \overline{Q} = 0\) 保持原态 -
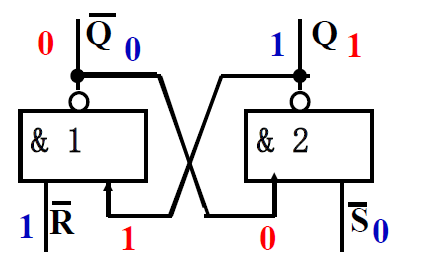 - 若原状态: \(Q = 0, \overline{Q} = 1\) 输出: \(Q = 1, \overline{Q} = 0\) 置 1
-
- 若原状态: \(Q = 0, \overline{Q} = 1\) 输出: \(Q = 1, \overline{Q} = 0\) 置 1
- 
-
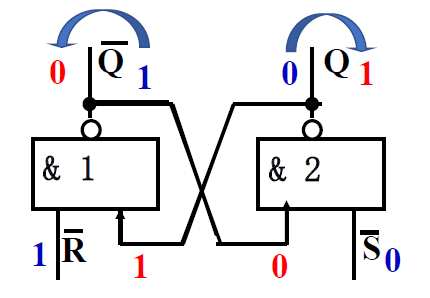
输入\(\overline{R} = 0, \overline{S} = 0 \textcolor{orange}{(S=R=1)}\)时, 不论原态如何, 输出全为 1, \(Q = \overline{Q}=1\)
-
 - 当\(\overline{R} = \overline{S} = 0时, Q = \overline{Q}=1\)违背互补输出的条件, 所以不允许\(\overline{R} = \overline{S} = 0\) 同时输入, 违背状态
- 当\(\overline{R} = \overline{S} = 0\)同时转变为 1 是, 翻转快的门输出先变为 0, 另一个此时维持为 1, 状态不定
- 当\(\overline{R} = \overline{S} = 0时, Q = \overline{Q}=1\)违背互补输出的条件, 所以不允许\(\overline{R} = \overline{S} = 0\) 同时输入, 违背状态
- 当\(\overline{R} = \overline{S} = 0\)同时转变为 1 是, 翻转快的门输出先变为 0, 另一个此时维持为 1, 状态不定 -
注意: 与非门实现的 RS 触发器为==低电平有效==
或非门实现的 RS 触发器为==低电平有效==
-
-
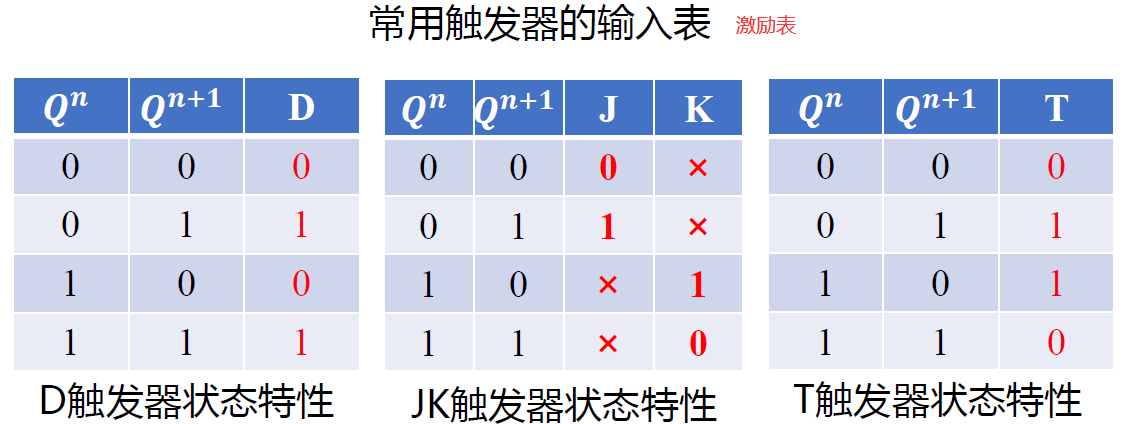
描述方法
-
功能表: 反映触发器在不同输入下对应功能的表格 低电平有效
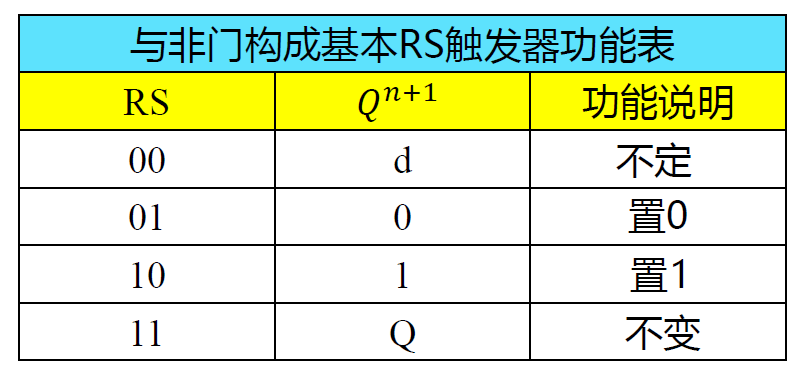
-
次态卡诺图: 根据触发器的功能表/状态表 得到的反映触发器次态和现态以及输入关系的卡诺图
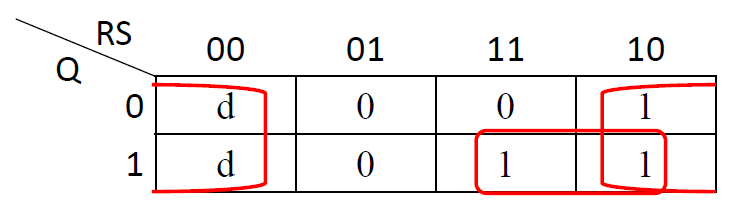
-
次态方程(特性方程) : 反应触发器次态和现态 以及输入关系的表达式 (根据卡诺图化简而来)
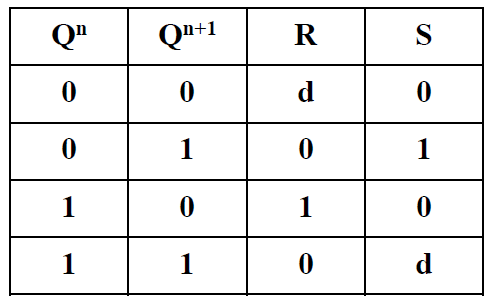
- 次态方程: \(Q^{n+1} = \overline{S} + RQ^n\) - 约束方程: \(R+S = 1\)
-
状态图: 反映触发器两种状态之间转移关系的有向图
- 圆圈表示稳定状态 (起点: 现态, 终点: 次态) - 有向线段表示状态转移方向 触发条件 -
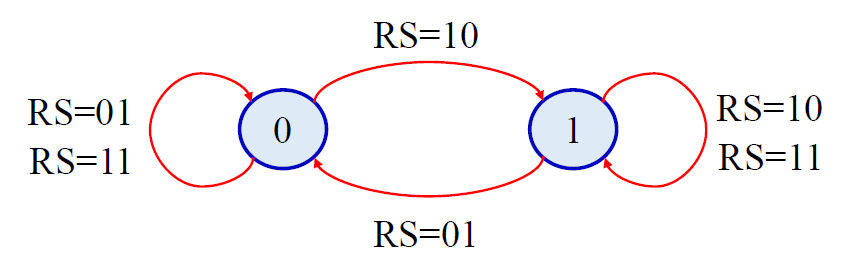
-
状态表: 反应触发器在输入作用下 现态与次态之间的转移关系 \(Q^n + RS \Rightarrow Q^{n+1}\)
-
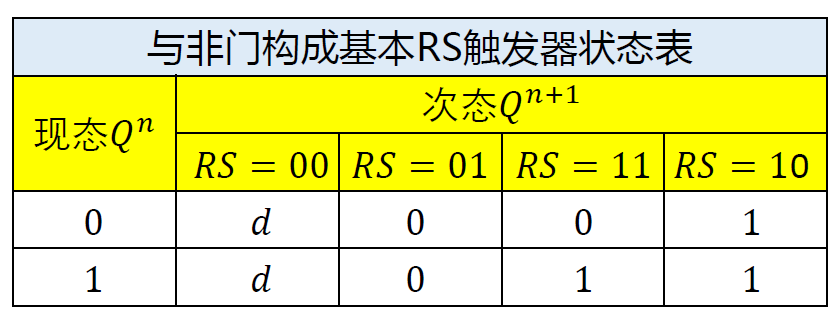
-
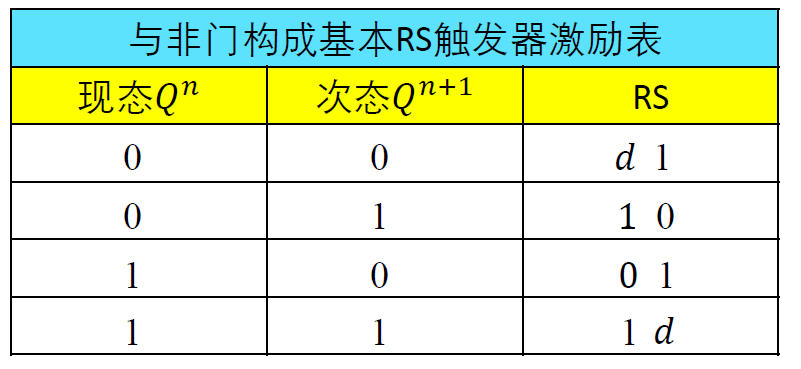
激励表: 反映触发器从现态\(Q^n\)转移到某种次态\(Q^{n+1}\)时, 对输入信号的要求 \(Q^n +Q^{n+1}\Rightarrow RS\)
-
-
时序图: 注意: 图上为\(\overline{R}和\overline{S}\) 低电平有效
-
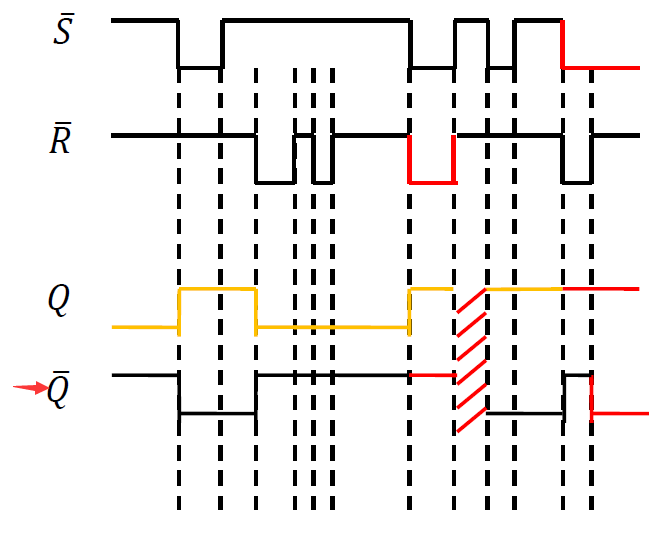
-
5.1.2 常用的时钟控制触发器¶
一. 简单结构的钟控触发器¶
1. 钟控 R-S 触发器¶
-
引入: 基本 RS 触发器
- 优点: 结构简单。它不仅可作为记忆元件独立使用,而且由于它具有==直接复位. 置位== 功能,因而被作为各种性能完善的触发器的基本组成部分。
- 缺点:
- S 和 R 端不能同时有效, 实际中不能保证这种情况一定不出现
- 只要输入变化, 状态就会改变
- 解决办法: 加入电平控制信号->钟控触发器
-
钟控 RS 触发器的结构和工作原理
-
在基本 RS 触发器的基础上增加一个时钟控制端 变成高电平有效 ① 提高触发器的抗干扰能力 ② 多个触发器在同一个控制信号的作用下同步工作
- 逻辑图:
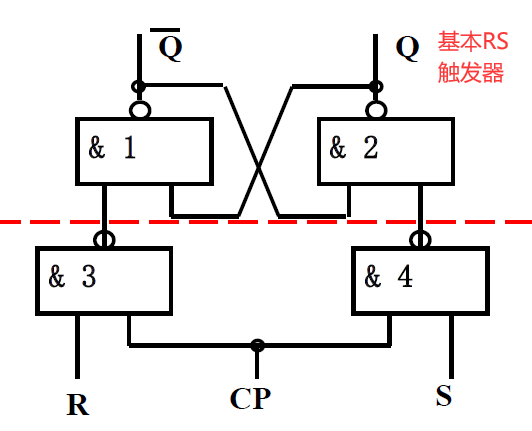 符号:
符号:  - R: Reset 清零端
S: Set 置 1 端
OP: Clock pulse 时钟脉冲
- R: Reset 清零端
S: Set 置 1 端
OP: Clock pulse 时钟脉冲 -
状态变化
1. > CP=0 时, 相当于 RS 中的\(\overline{R} = \overline{S} = 1\), 保持原态
- <img src="数字电路与逻辑设计.assets\image-20221018162747811.png" alt="image-20221018162747811" style="zoom: 33%;"/>2. > CP=0 时, 经过与非操作, RS 高电平有效 , 类似或非门耦合的 RS 触发器
- <img src="数字电路与逻辑设计.assets\image-20221018173708200.png" alt="image-20221018173708200" style="zoom: 33%;"/>
-
-
描述
-
真值表->功能表
1. CP=0, 电路保持不变, \(Q^{n+1} = Q^n\) 2. CP=1, 如下 -
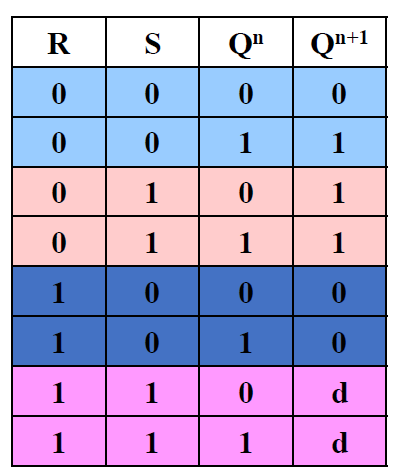
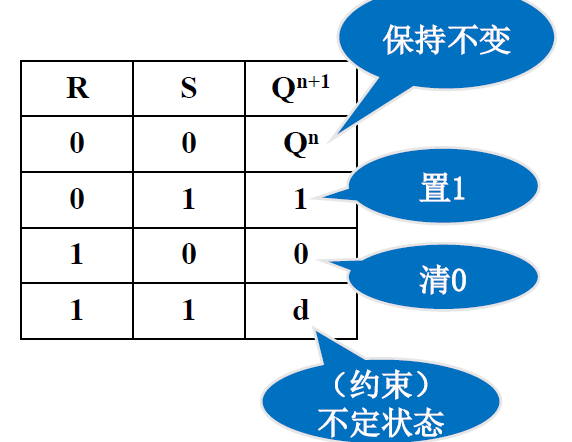
-
次态卡诺图和次态方程 -
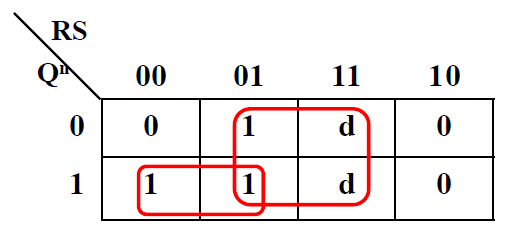 - CP=0 时, \(Q^{n+1} = Q^n\)
- CP=1 时, \(\textcolor{#66ccff}{Q^{n+1} = S + \overline{R}Q^n}, 约束方程: RS=0\) 和 或非门构成的 RS 触发器特性方程一致, 高电平有效
- CP=0 时, \(Q^{n+1} = Q^n\)
- CP=1 时, \(\textcolor{#66ccff}{Q^{n+1} = S + \overline{R}Q^n}, 约束方程: RS=0\) 和 或非门构成的 RS 触发器特性方程一致, 高电平有效 - 激励表
- 状态图和状态表
-

- 时序图: CP = 1 时, 高电平有效, R 为清零端(复位端); S 为置 1 端 CP=0 时, 维持原态
-
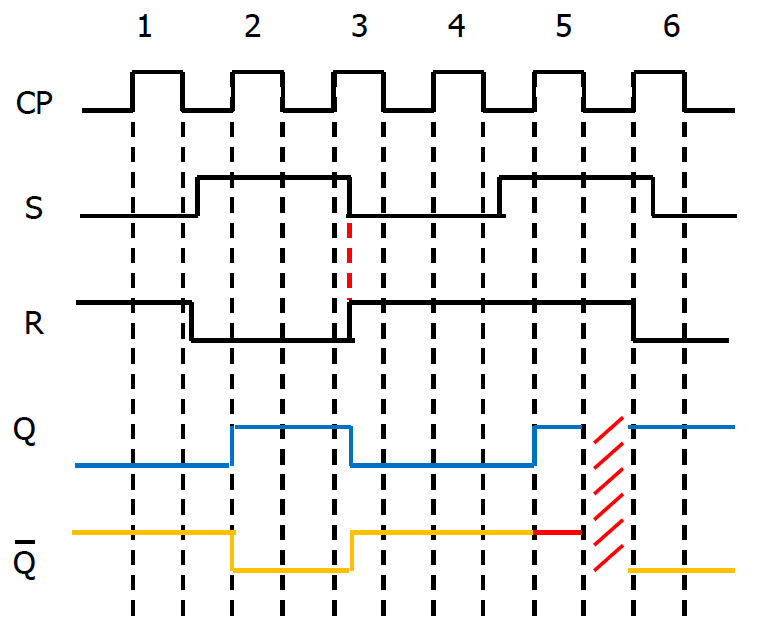
-
-
钟控 RS 触发器存在的问题
-
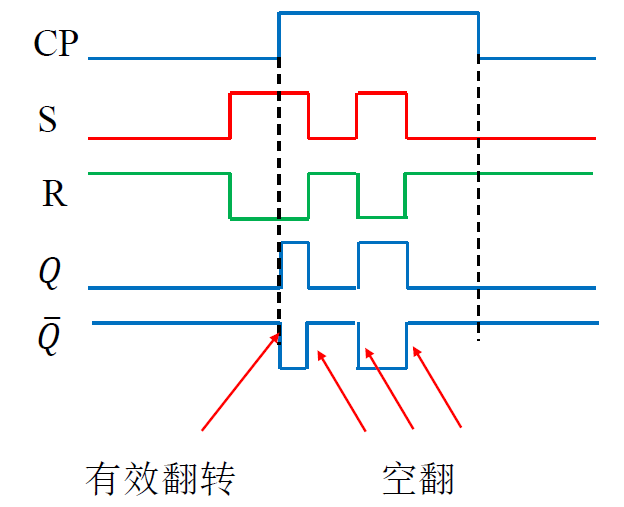
空翻
- 在一个时钟脉冲周期内, 触发器发生多次翻转 (不应该出现)
*
-
当 R = S = 1 时, 依然会出现不定状态
-
-
钟控 RS 触发器 小结
- 电路加了一级门电路,用 CP 进行统一控制,有效地提高了电路的可靠性,但存在空翻现象;
- 电路仍存在不定状态,即使用时,需要约束条件。为了解决不定状态,采用让两路数据成为互补的数据,从根本上解决相同信号。 改进的电路如下几种: - 钟控 D 触发器 - 钟控 JK 触发器 - 钟控 T 触发器 - 钟控 T’ 触发器
2. 钟控 D 触发器¶
-
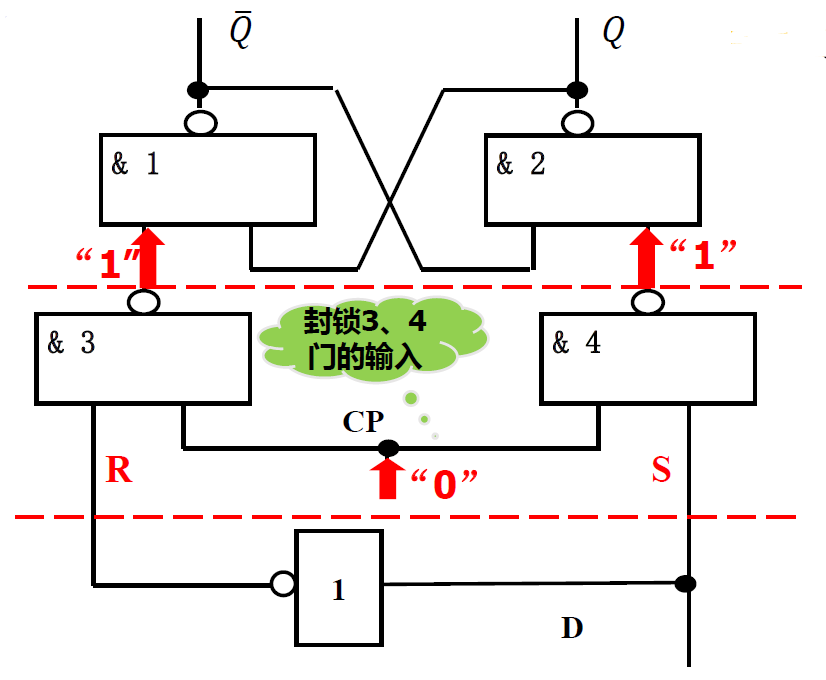
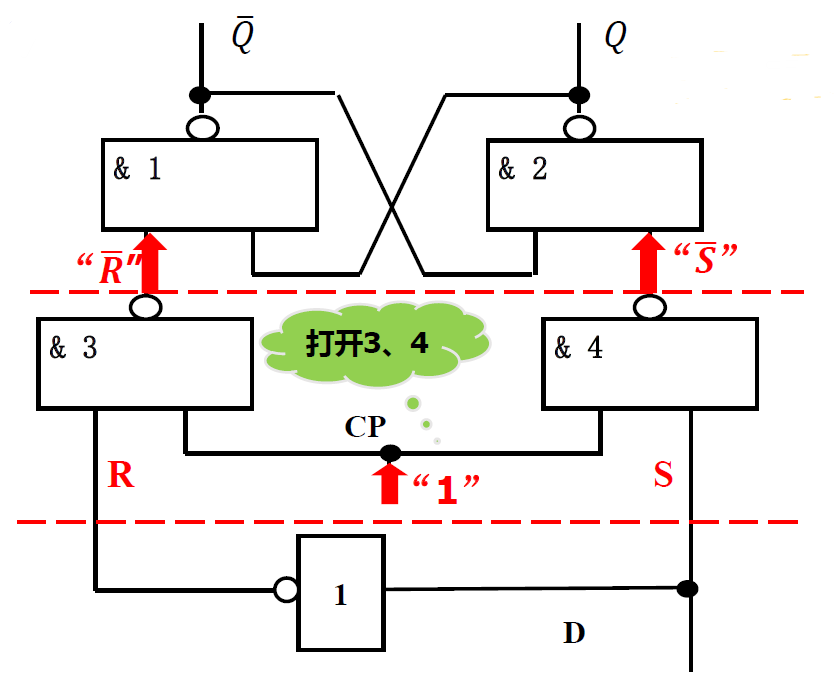
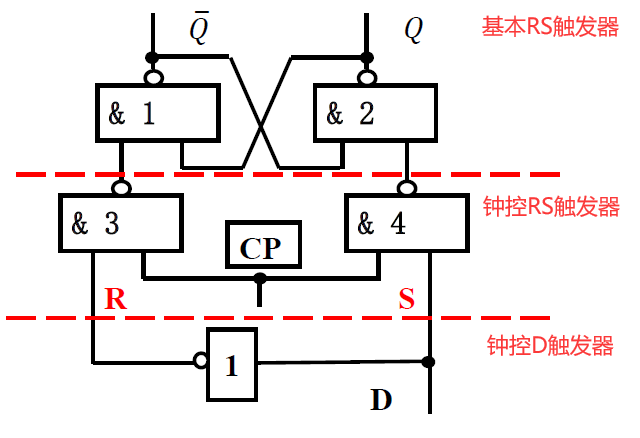
D 触发器: 在钟控 RS 基础上, 将输入改为一个信号 D 控制, S 接信号 D, R 接\(\overline{D}\) 实现信号的互补输入
- 逻辑图:
 符号图:
符号图: 
- 逻辑图:
-
状态变化
-
CP = 0 时, 保持原态
-
CP=1 时, $Q^{n+1} = S + \overline{R}Q^n, S = D, R = \overline{D} $
-
-
次态方程, 真值表和功能表
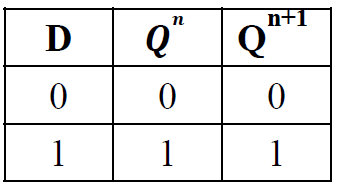
-
CP=0 时, 电路静止, \(Q^{n+1} = Q^n\)
CP=1 时, \(\begin{cases}Q^{n+1} = S + \overline{R}Q^n \\ S = D, R = \overline{D} \end{cases}\Rightarrow \textcolor{#66ccff}{ Q^{n+1} = D}\)
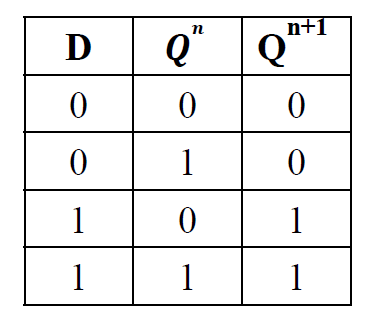
->
-
-
状态表和状态图
- 当 CP=1 时, 状态表和状态图如下 :
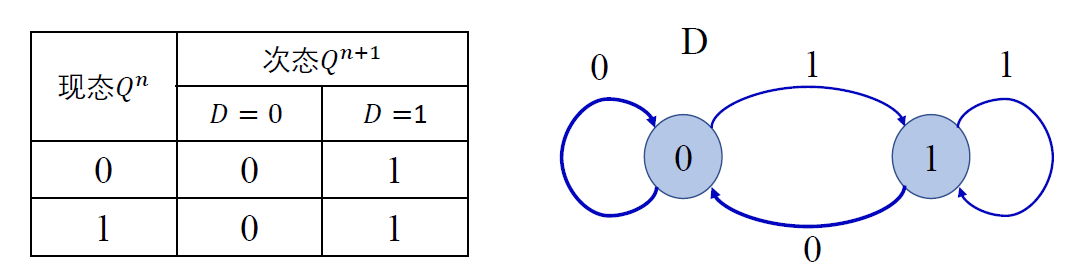
- 当 CP=1 时, 状态表和状态图如下 :
- 时序图
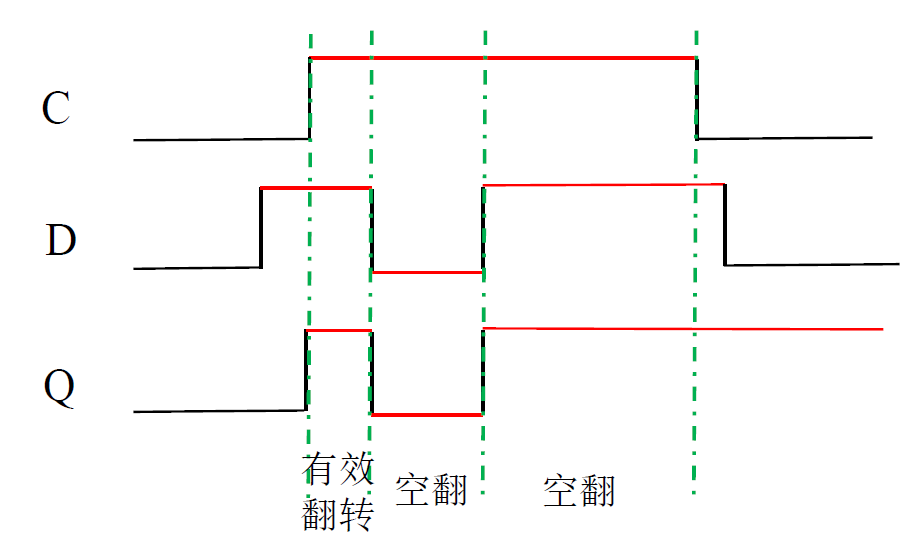 依然存在空翻现象
依然存在空翻现象
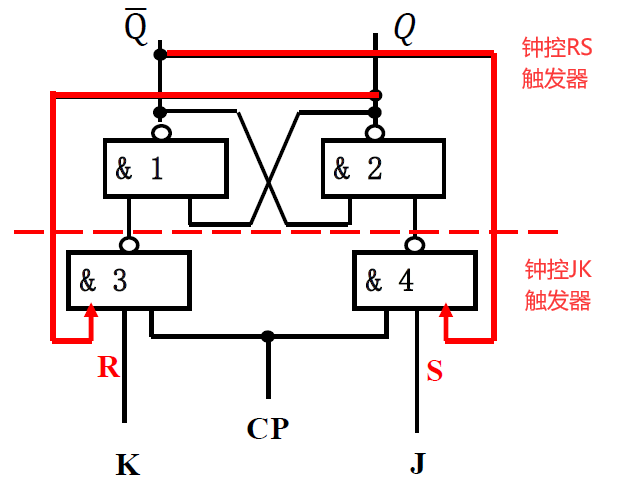
3. 钟控 JK 触发器¶
-
在钟控 R-S 基础上添加了反馈; 设置信号 J 接到 S, 信号 K 接到 R (S->J K->R)
- 逻辑图:
 符号:
符号: 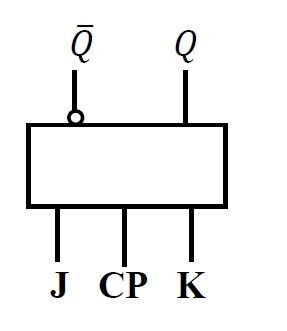
- 逻辑图:
-
状态变化
-
CP=0, 保持原态
-
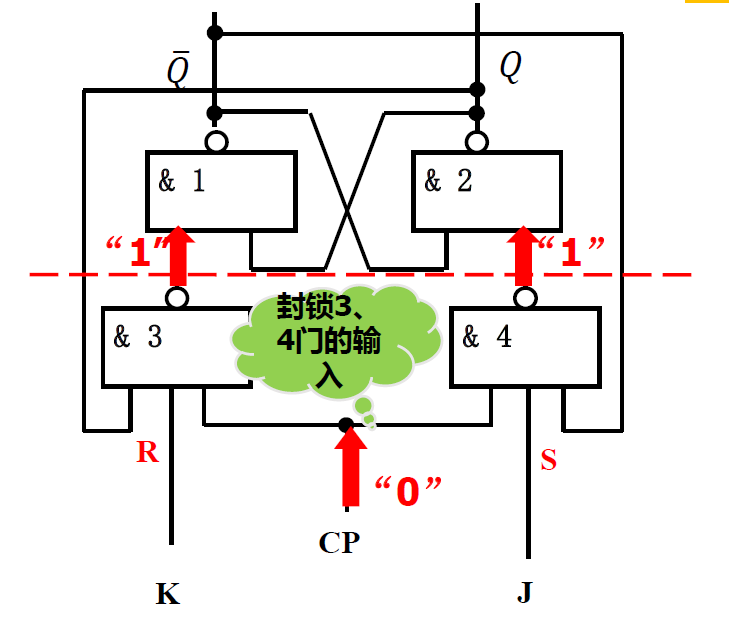
-
CP=1
1. > J=K=0 保持不变
- <img src="数字电路与逻辑设计.assets\image-20221018194825073.png" alt="image-20221018194825073" style="zoom: 33%;" />2. > K = 1 J = 0 清 0
- <img src="数字电路与逻辑设计.assets\image-20221018195800080.png" alt="image-20221018195800080" style="zoom: 33%;" />3. > K = 0 J = 1 置 1
- <img src="数字电路与逻辑设计.assets\image-20221018200435708.png" alt="image-20221018200435708" style="zoom: 33%;" />4. > J=1 K=1 翻转
- <img src="数字电路与逻辑设计.assets\image-20221018200634625.png" alt="image-20221018200634625" style="zoom: 33%;" /> -
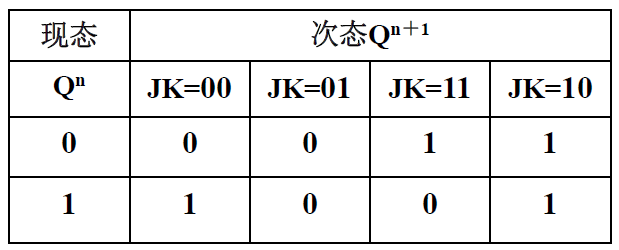
真值表和功能表
- CP=0 时, 电路静止, \(Q^{n+1} = Q^n\)
- CP=1 时, 如下
<img src="数字电路与逻辑设计.assets\image-20221018200929718.png" alt="image-20221018200929718" style="zoom:50%;" /> $\Rightarrow$ <img src="数字电路与逻辑设计.assets\image-20221018201011834.png" alt="image-20221018201011834" style="zoom:50%;" /> -
次态卡诺图 次态方程
-
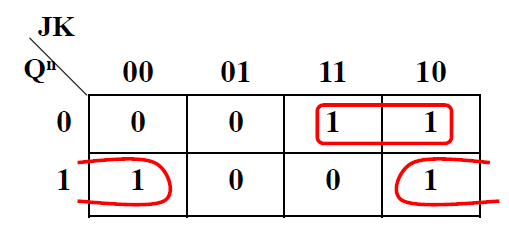
- CP=0 时, \(Q^{n+1} = Q^n\)
CP=1 时, <font color='#66ccff'>$Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n$</font> <font color='orange'>跟异或门很相似</font> -
激励表
-
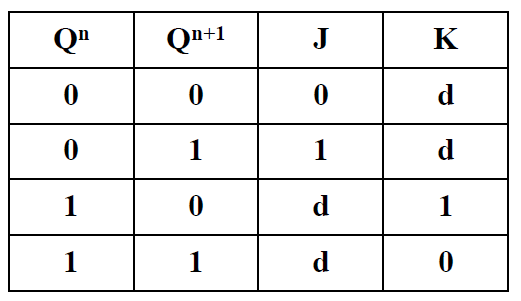
-
状态图 状态表
-
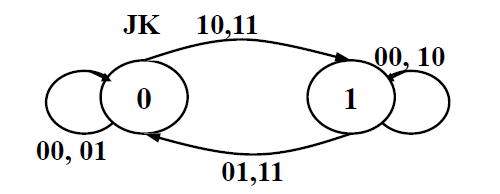 -
- 
-
时序图 -
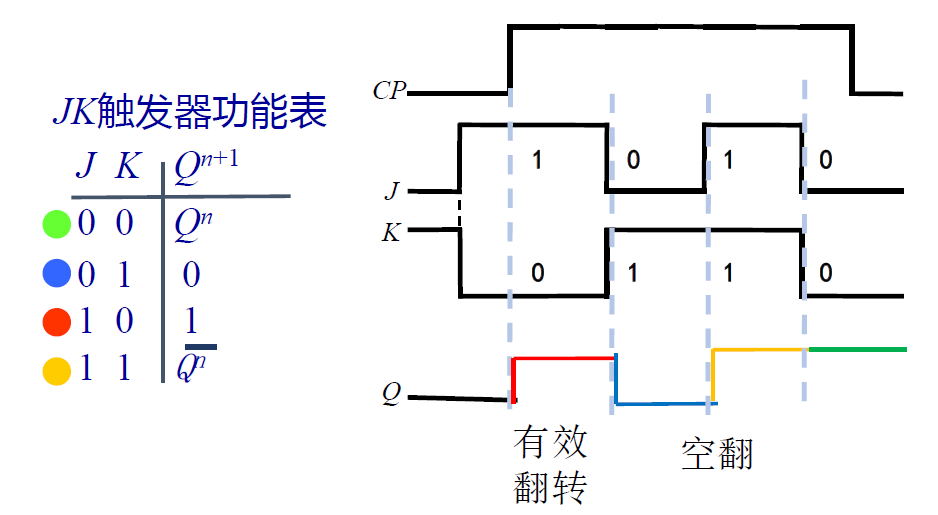 - 依然存在空翻现象
- 依然存在空翻现象
-
4. 钟控 T 触发器¶
-
钟控 T 触发器 : 在 JK 触发器上, 把 J 端和 K 端直接相连, 形成 T 端
- 逻辑图:
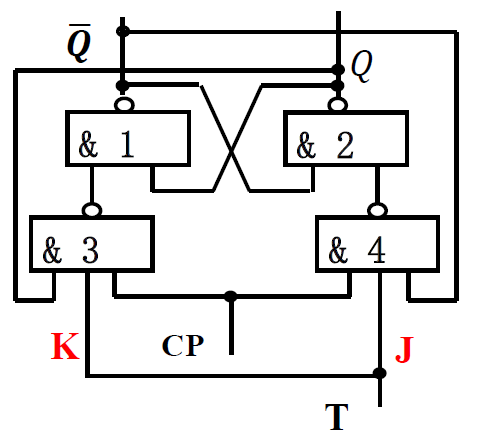 符号:
符号: 
- 逻辑图:
-
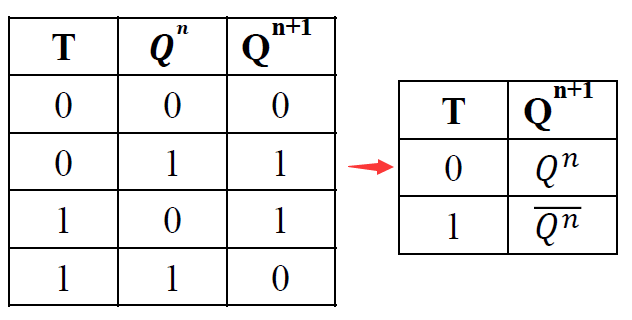
次态方程, 真值表和功能表
- CP=0 时 电路静止, \(Q^{n+1} = Q^n\)
- CP=1 时 \(\begin{cases}Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n\\ J=K=T\end{cases} \Rightarrow \textcolor{#66ccff}{Q^{n+1} = T\overline{Q^n} + \overline{T}Q^n = T\oplus Q^n}\)
- 真值表:
-
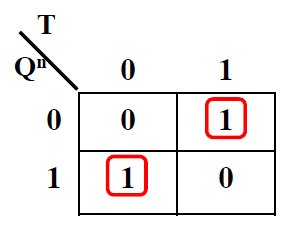
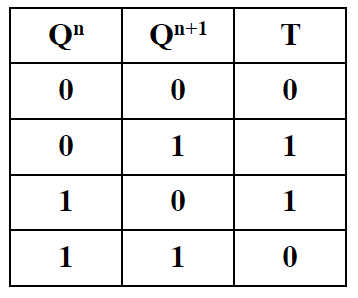
次态卡诺图和激励表
- 卡诺图:
- 激励表:
- 卡诺图:
-
状态表和状态图
-
CP=1 时, 状态表和状态图如下
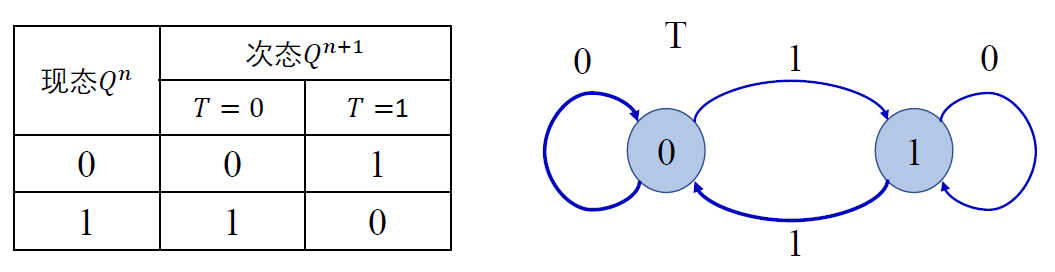
-
T’触发器¶
- T′触发器又叫计数器,一个时钟周期到来,在上升沿到来实现对原状态的反转,那么每次上升沿到来都对原状态进行反转就可以实现计数。
- 相当于 T 触发器中 T=1
5. 钟控触发器总结¶
- 空翻 : 同一时钟脉冲作用期间触发器状态发生两次或多次变化的现象
- 空翻原因
- 时钟脉冲作用期间,输入信号直接控制着触发器状态的变化
- CP 为 1 时,输入信号发生变化,触发器状态就会发生变化
- 时钟宽度控制不够
- CP 为 1 时间过长,输入的多次变化得到完全响应,使得一个时钟脉冲作用期间触发器多次翻转。
- 时钟脉冲作用期间,输入信号直接控制着触发器状态的变化
- 解决方法:
- 主从触发器 (不常用, 自学)
- 边沿触发器
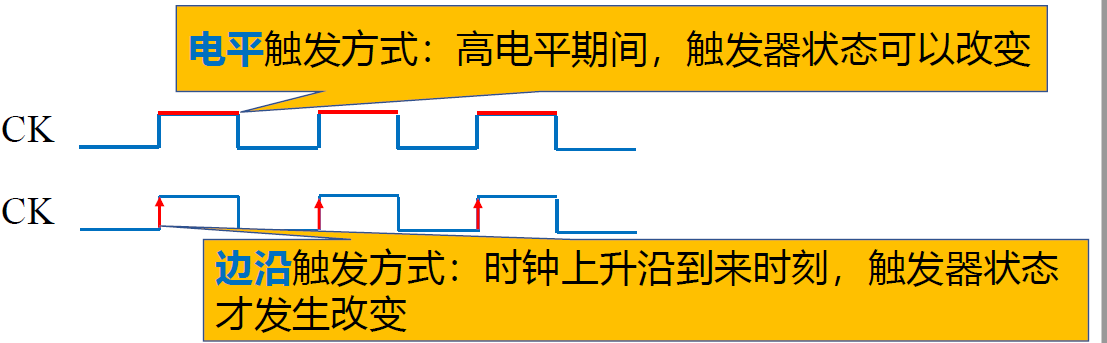
二. 边沿触发器¶
- 边沿触发器: 边沿触发器的状态改仅出现在时钟脉冲的==上升沿== 或者==下降沿== 上,而在时钟稳定的 0 或 1 期间,输入信号都不能进入触发器。在出现上升沿 / 下降沿时对输入进行采样
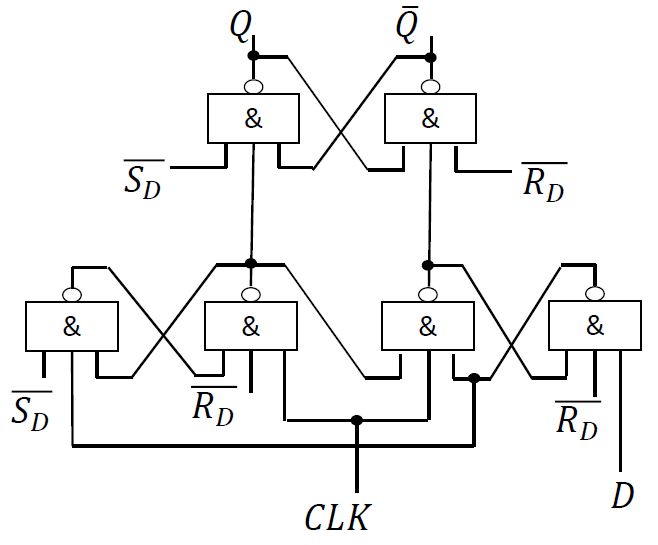
1. 边沿 D 触发器 7474¶
-
逻辑图 :
 符号 :
符号 : 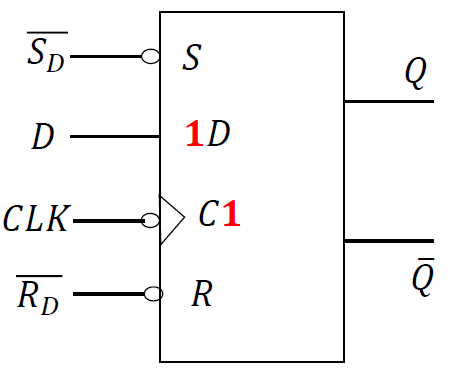
- \(\overline{R_D}直接置'0'端;\quad \overline{S_D}直接置'0'端\)
-
区分边沿信息
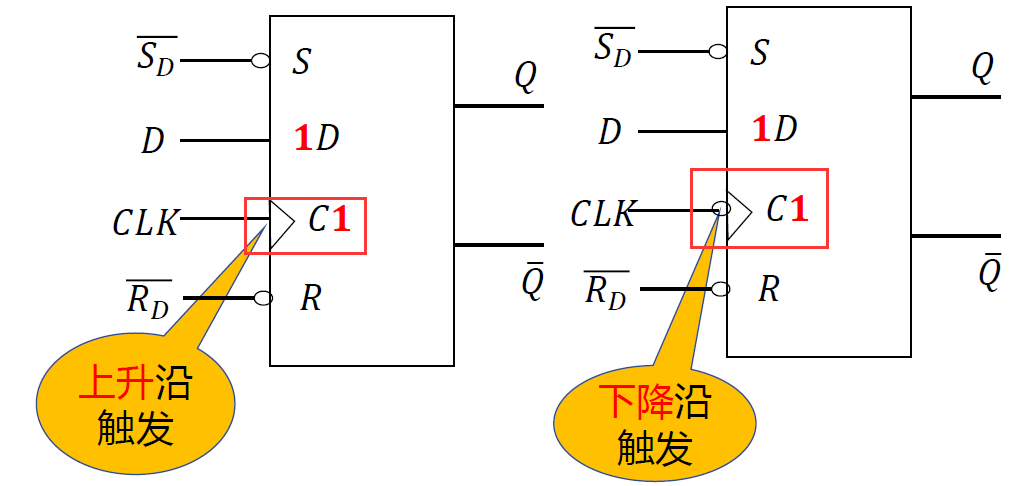
-
原理
-
设\(\overline{S_D} = \overline{R_D} = 1\) 并且==CLK=0==
-
Qn = 1 / 0: 保持不变
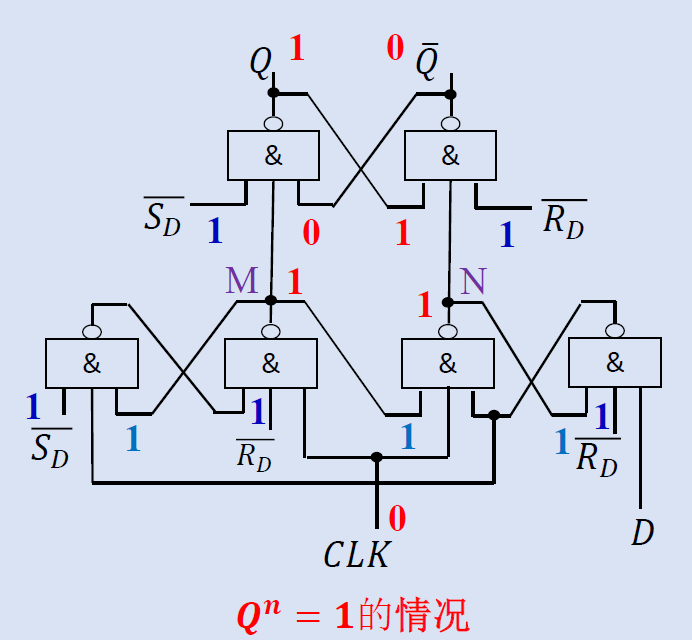
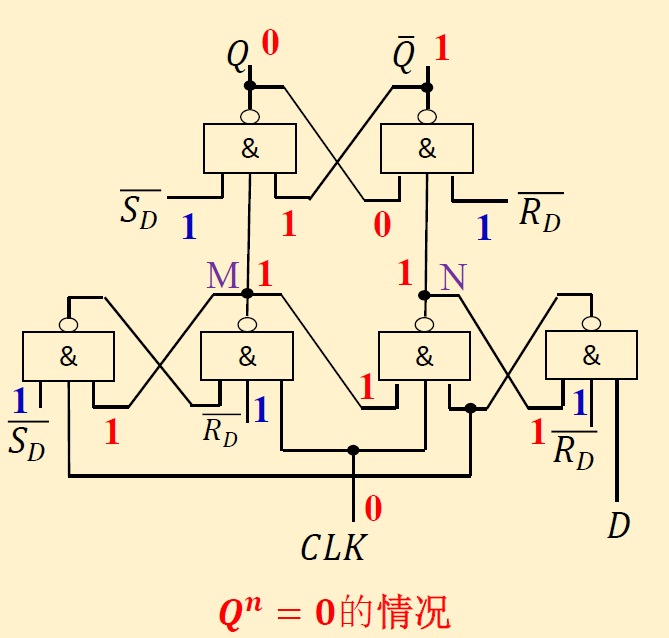
M=N=1, 输出 Q 保持不变
-
CLK 由 0==变成== 1 时
-
D = 0 / 1
-
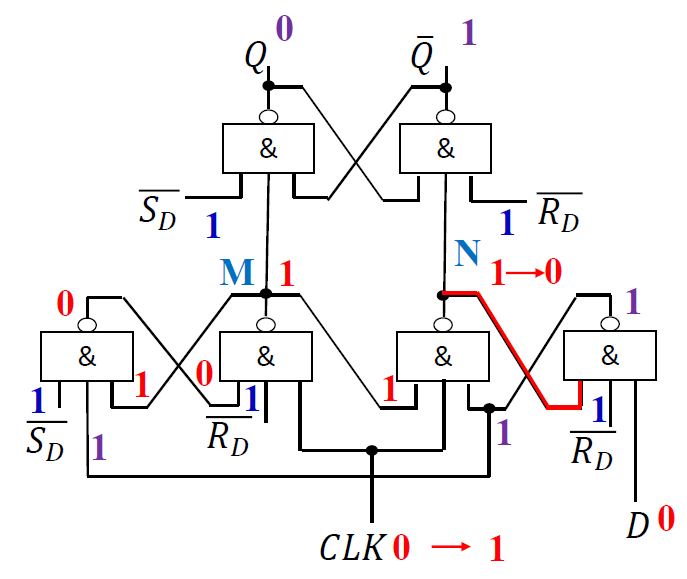
如果在上升沿过后,CLK=1 期间,输入 D 发生变化,但由于 N=0 ,输入变化不发生作用。
-
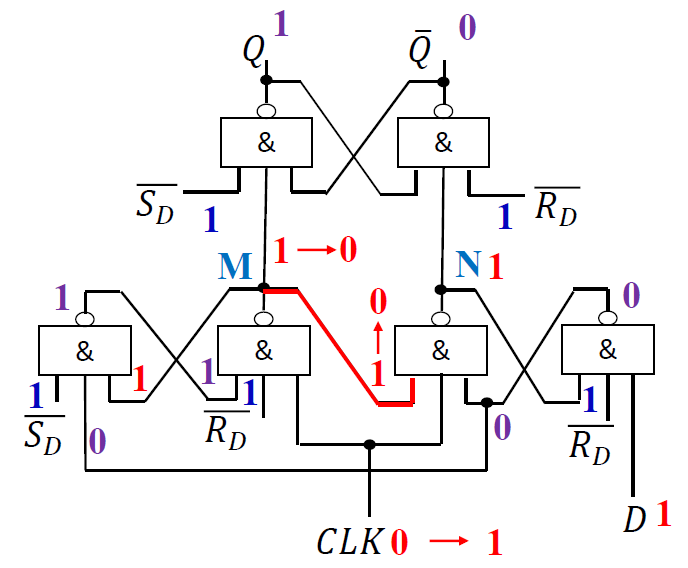
如果在 CLK=1 期间,输入 D 发生变化,但由于 M=0 ,导致 M 和 N 不会变化,因此输入不变化会输出不会发生变化
- \(Q^{n+1} = D = 1\)
-
-
-
-
特性表&特性方程
-
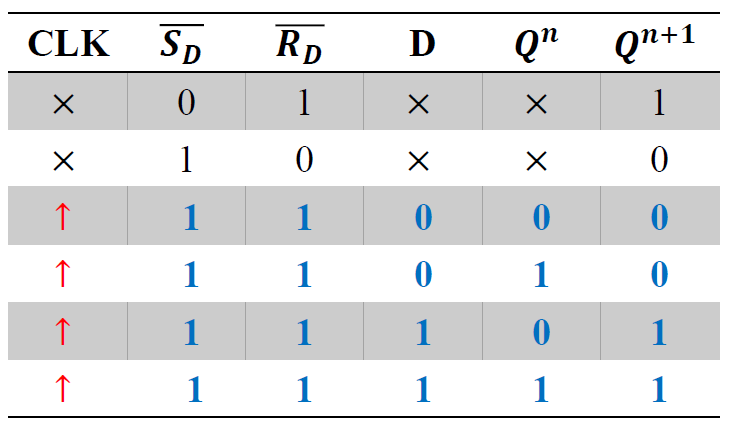 ↑表示上升沿触发
- 特性方程: \(Q^{n+1} = D\)
- D 触发器最简单, 应用最广
↑表示上升沿触发
- 特性方程: \(Q^{n+1} = D\)
- D 触发器最简单, 应用最广 -
时序图
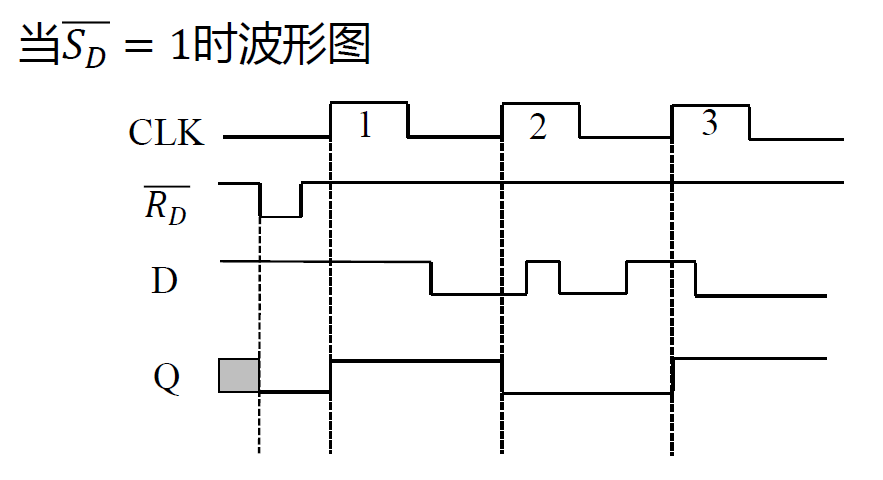
-
2. 边沿 JK 触发器¶
-
下降沿 JK 触发器逻辑原理图 (JK: \(Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n\))
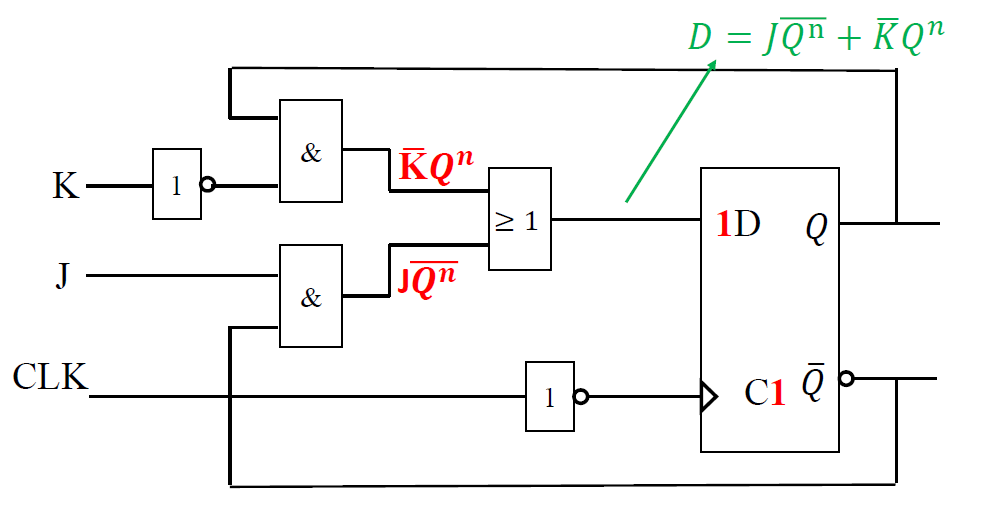 下降沿, 在 CLK 上加了个非门
下降沿, 在 CLK 上加了个非门
-
下降沿 JK 触发器符号:
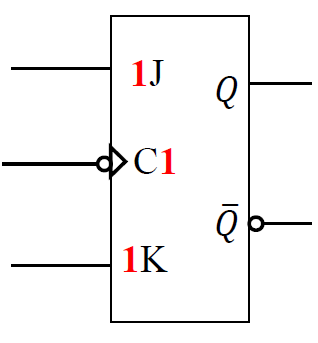
- 下降沿 JK 触发器特性表
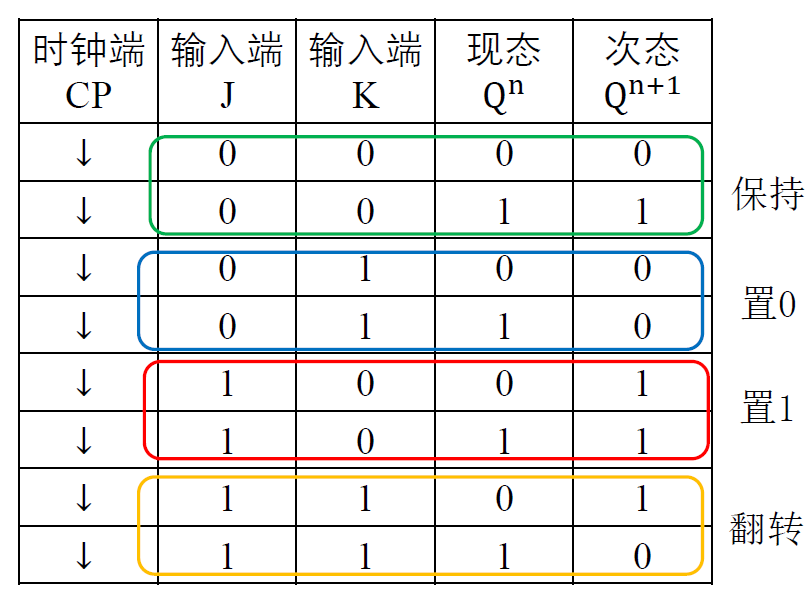
- 功能最齐全, 并且输入没有约束
- 时序图
- 下降沿 JK 触发器时序图 :
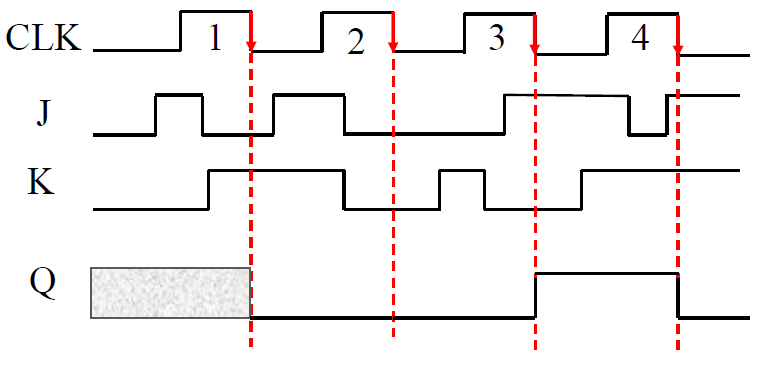
- 上升沿 JK 触发器时序图 :
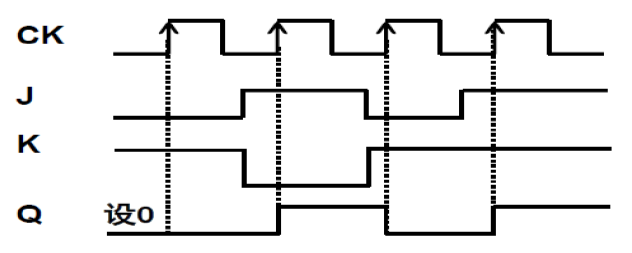
- 下降沿 JK 触发器时序图 :
5.1.3 不同触发器转换¶
-
目的: 在已有触发器的基础上,通过增加附加转换电路,使之转变成另一类型的触发器
- 触发器转换 结构示意图:
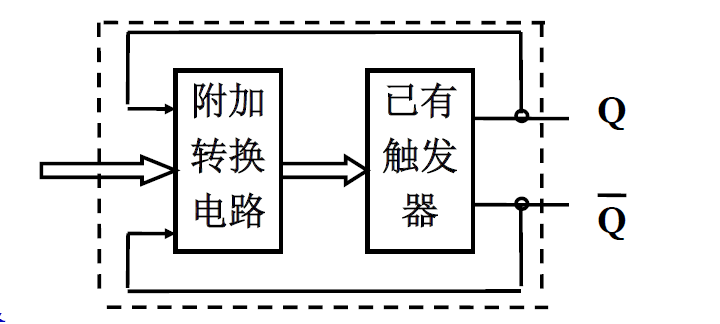
- 触发器转换 结构示意图:
-
转换方法
- 公式法: 利用两个触发器的特性方程, 联立比较, 转换电路表达式 (常用)
- 图表法: 对比两个触发器的激励表, 列出转换电路的真值表, 求出逻辑表达式
-
代数法
-
例: JK 触发器转换成其他类型触发器
1. > JK 型转 D 型触发器
- JK 触发器公式: $Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n$ - D 触发器公式: $Q^{n+1} = D = DQ^n + D\overline{Q^n}$ - $J=D; K=\overline{D}$2. > JK 型转 T 型触发器
- T 型触发器公式: $Q^{n+1} = T\overline{Q^n} + \overline{T}Q^n$ - $J = K = T$3. > JK 型转 RS 型触发器
- JK 型触发器本身就具有 RS 型的所有功能, 只需要令 J=S, K=R 即可 -
例: D 触发器转换成其他类型触发器 (直接用组合电路表示出需要的公式)
1. > D 型转 JK 型触发器
- JK 触发器公式: $Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n$ - D 触发器公式: $Q^{n+1} = D$ - $D = J\overline{Q^n} + \overline{K}Q^n$2. > D 型转 RS 型
- RS 触发器公式: $Q^{n+1} = \overline{S} + RQ^n$ - $D = \overline{S} + RQ^n$3. > D 型转 T 型
- T 型触发器公式: $Q^{n+1} = T\oplus Q^n$ - $D = T\oplus Q^n$
-
-
卡诺图法
-
T 触发器转 JK 型触发器
-
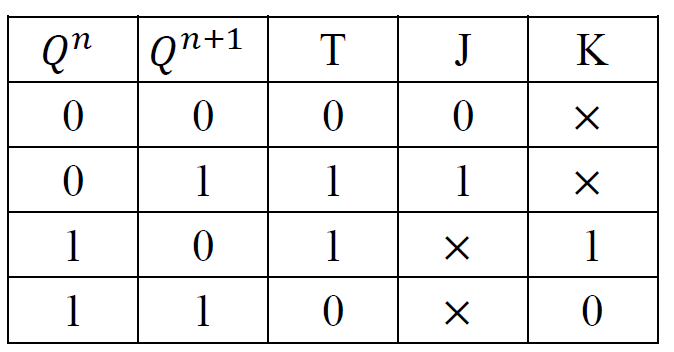 \(T = f(J, K, Q^n)\)
-
\(T = f(J, K, Q^n)\)
- 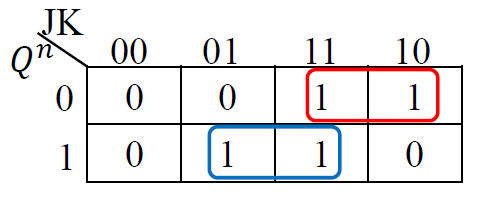 - \(T = J\overline{Q^n} + KQ^n\)
- \(T = J\overline{Q^n} + KQ^n\) -
T 触发器转 RS 触发器
-
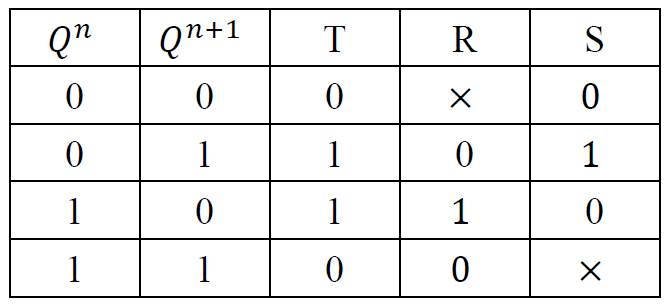 \(T = f(R, S, Q^n)\)
-
\(T = f(R, S, Q^n)\)
-  - \(T = S\overline{Q} + RQ^n\)
- \(T = S\overline{Q} + RQ^n\)
-
5.1.4 触发器的应用¶
-
开关消颤
 由于机械弹性作用,机械式开关在使用中,通常伴随有一定时间的触点机械抖动。触电抖动可能导致判断出错(一次按下或释放被错误地认为是多次操作)
由于机械弹性作用,机械式开关在使用中,通常伴随有一定时间的触点机械抖动。触电抖动可能导致判断出错(一次按下或释放被错误地认为是多次操作)-
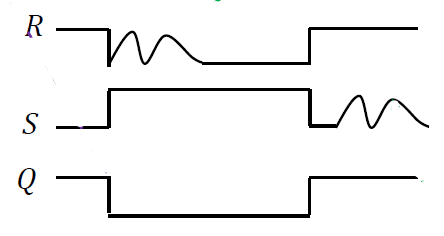
基础 RS 结构触发器只对$\overline{R}$的第一次**负跳变**响应<font color='orange'>(低电平有效,R=S=1 是维持原状,没有影响)</font>
-
分频 / 计数功能
- 分频: 将单一频率信号的频率降低为原来的\(\frac{1}{N}\)
- 计数: 用来统计输入脉冲的个数
- 电路图:

- \(Q^{n+1} = \overline{Q^n}\)
- 下一级的 CLK = \(\overline{Q}\)
- 时序图:

- 𝑄1 对 CLK 二分频 𝑄2 对 CLK 四分频 𝑄3 对 CLK 八分频
5.2 时序逻辑电路分析¶
5.2.1 时序逻辑电路概述¶
-
时序逻辑电路分类
-
按照输入的脉冲是否同步
- 异步时序逻辑电路 / 同步时序逻辑电路
- 同步: 存储电路里所有触发器有一个==统一的时钟源== ,它们的状态在同一时刻更新
异步: 没有统一的时钟脉冲或没有时钟脉冲电路的状态更新不是同时发生的。-
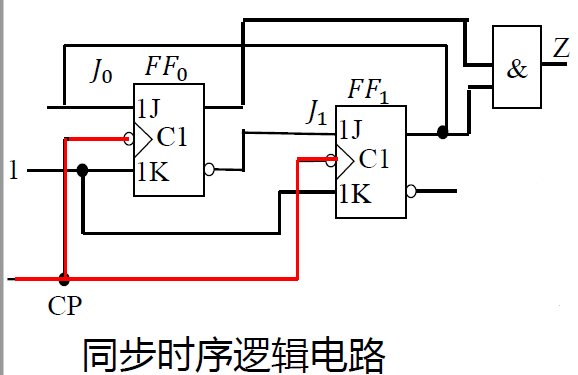
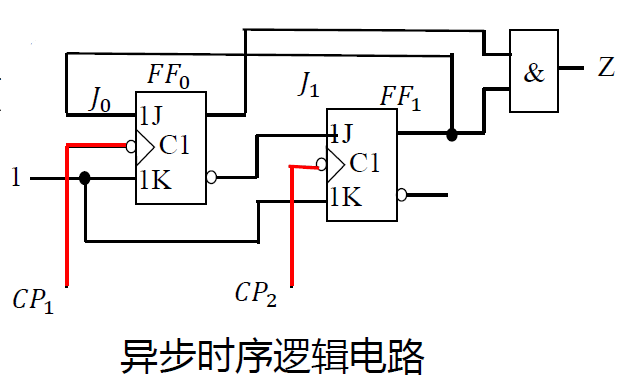
-
按照输入和输出关系 - 摩尔(Moore) 型电路 - 米里(Mealy) 型电路
-
5.2.2 同步时序逻辑电路¶
一. 同步时序逻辑电路特点¶
-
同步时钟信号
- 电路状态的改变依赖于输入信号和时钟脉冲信号
- 同步时序逻辑电路中触发器的状态变化是在 CP 脉冲作用下==同时发生== 的
- 同步时钟信号作为一种默认的==时间基准== 而非输入信号
-
- 现态:脉冲到来前电路触发器的状态 次态:脉冲到来后电路触发器的状态
-
对于同步时序逻辑电路,只需==根据当前状态下的输入== ,求得电路的 下一个状态 和 输出值
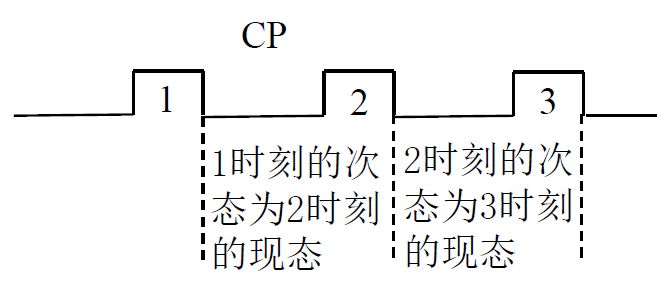
二. 同步时序逻辑电路分类¶
根据==输出信号== 的特点,又可将同步时序逻辑电路划分为摩尔(Moore )型和米里( Mealy )型
-
摩尔 Moore 型电路: 电路输出 Z 仅仅取决于各触发器的状态,输入只决定电路触发器的状态改变, 与输入无关
-
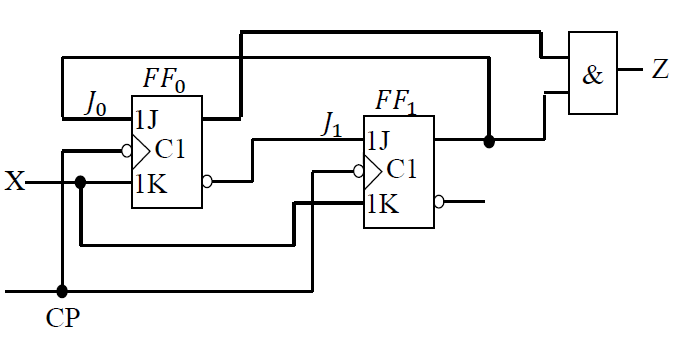
X 不直接影响输出 Z, Z 的值只取决于触发器状态\(Q_0^n和 Q_1^n\)
-
-
米里 Mealy 电路 : 电路的输出 Z 是输入变量 A 及触发器输出 Q1. Q0的函数,即当前的输入和当前的状态==共同决定== 当前的输入
-
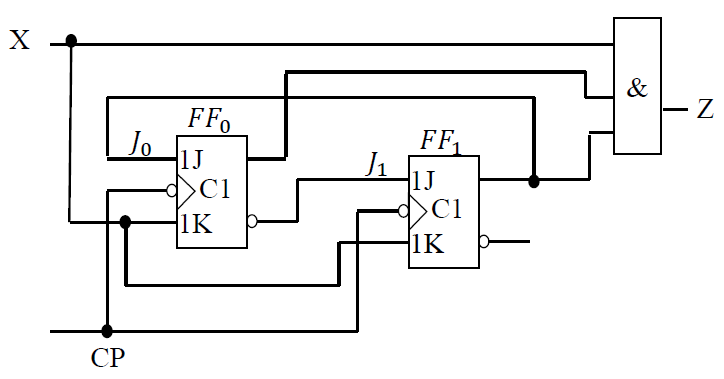
Z 的变化不仅与触发器当前的状态\(Q_0^n和 Q_1^n\) 有关,还与当前的输入 X 有关
-
-
Moore 型电路: \(所有的输入\Rightarrow 状态y \Rightarrow 输出\)
Mealy 型电路: \(\begin{cases}过去的输入\Rightarrow 状态y\\当前的输入\end{cases}\Rightarrow输出\)
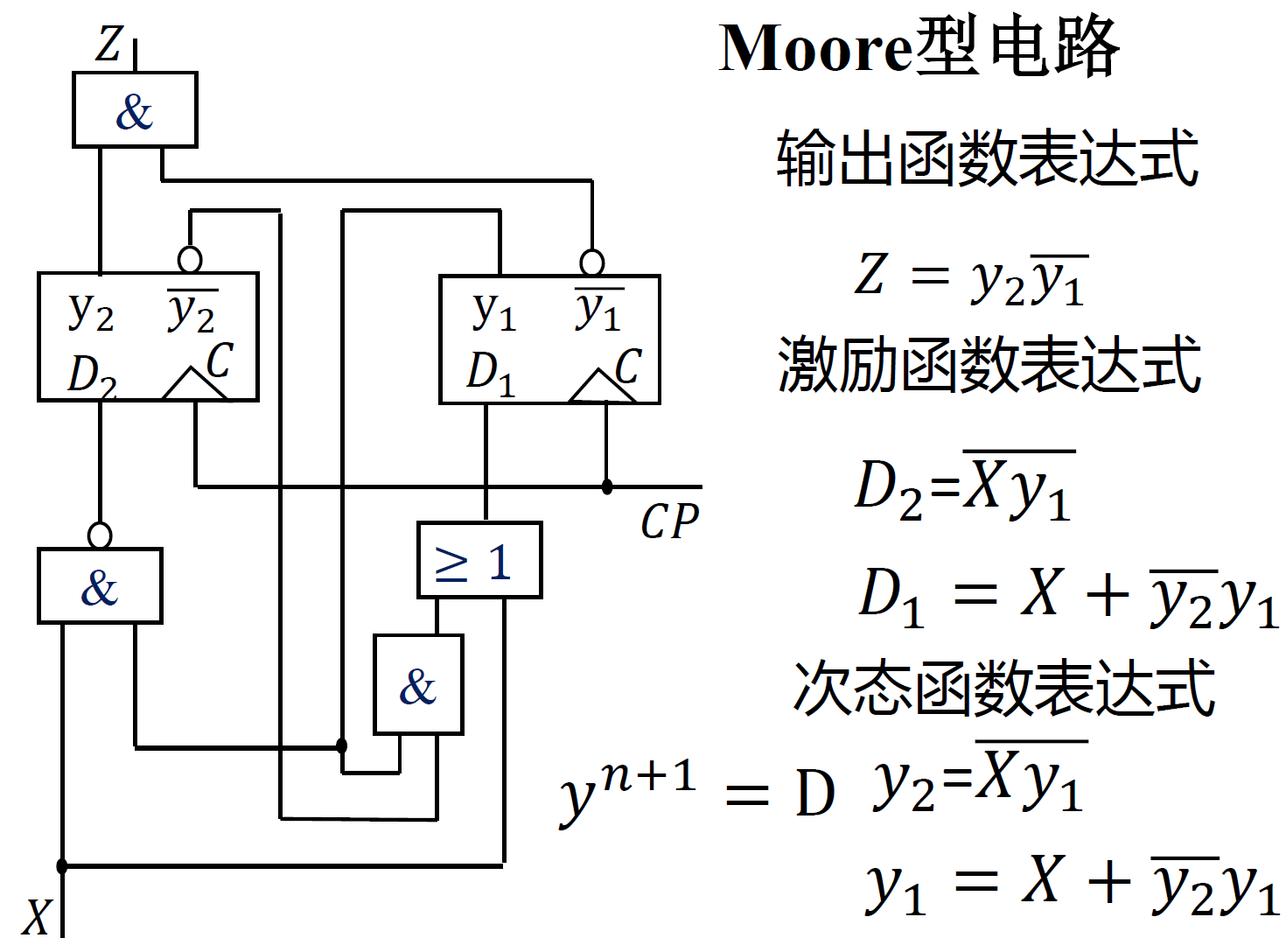
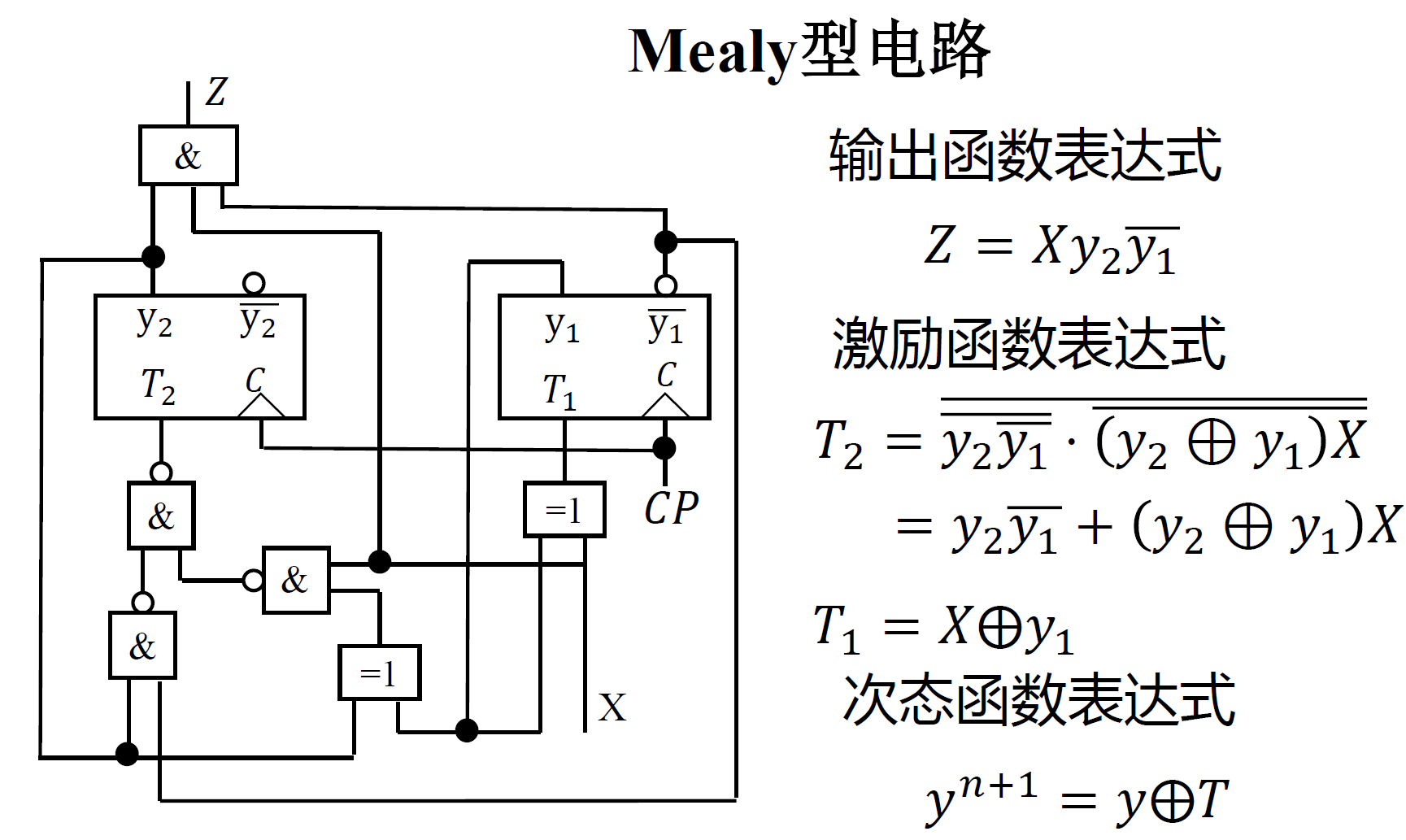
-
状态表 : 一种反映时序逻辑电路
输出Z .次态yn+1和电路输入x .现态y 之间关系的表格- 是同步时序逻辑电路分析和设计的常用工具
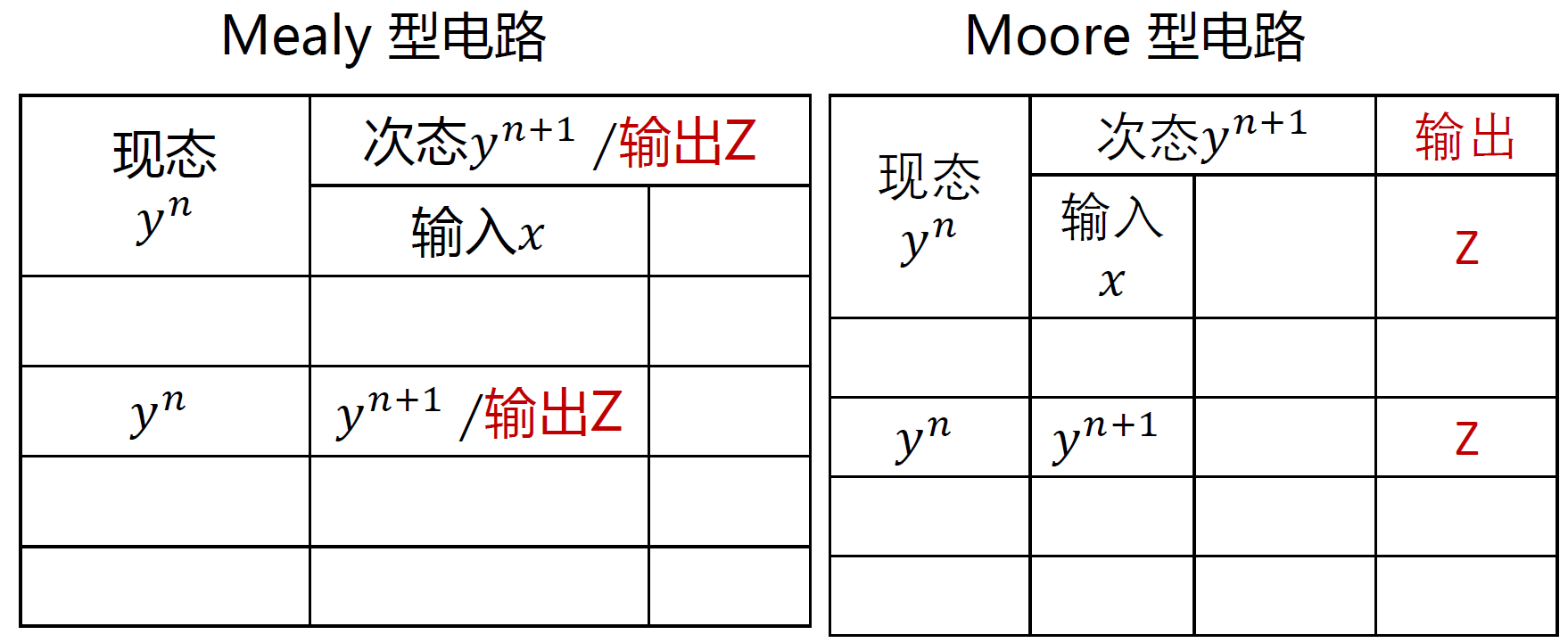
- Mealy的输出由当前状态(yn)和当前输入(X)共同决定
- Moore的输出仅由当前状态(yn)决定
-
状态图 : 一种反映时序逻辑电路状态 转移规律 及==相应输入/输出取值关系== 的有向图

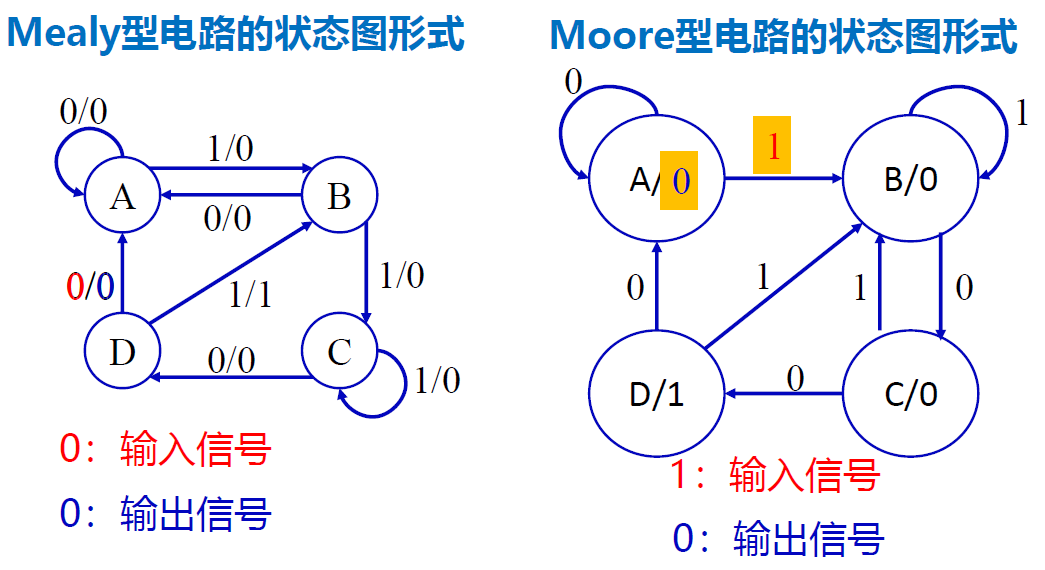
- Mealy 由于输出还受 X 影响, 输出 Z 需要写在 X 旁边, 形式为
X/Z - Moore 由于输出只受状态影响, 输出写在状态上即可
三. 同步时序逻辑电路分析¶
由于时序逻辑电路中的基本单元是触发器,加上同步时序逻辑电路中脉冲只作为时间基准,因此课程中讨论 基于触发器时序电路的分析方法 。
-
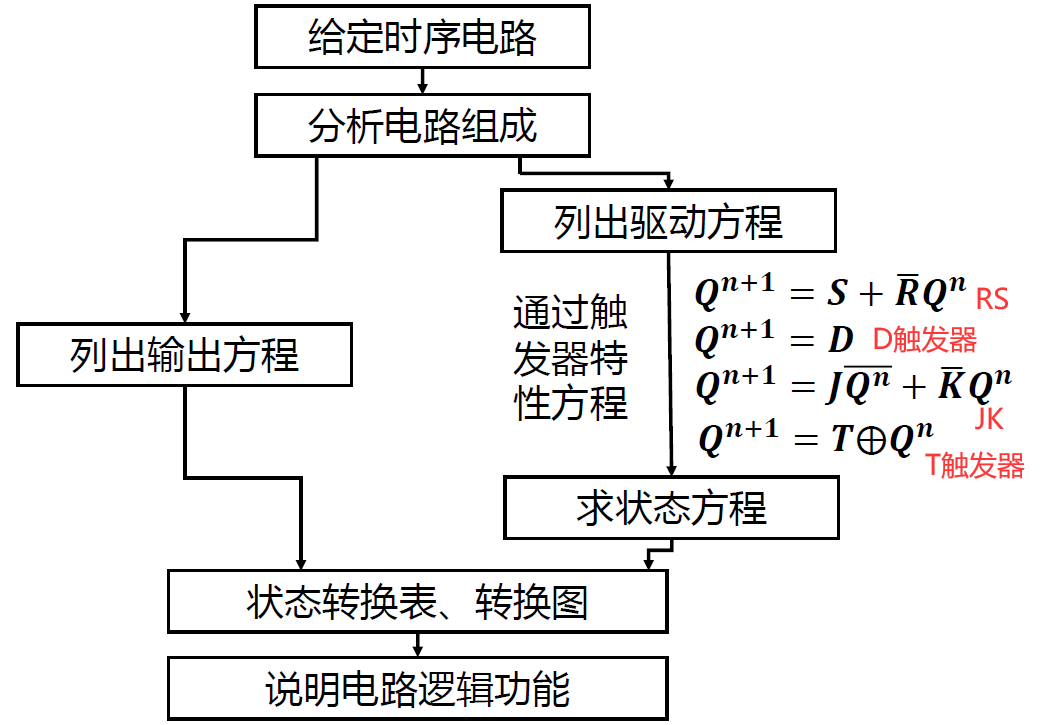
时序电路分析的步骤
-
\[ 逻辑电路图 \Rightarrow \begin{cases}驱动方程\\输出方程\\状态方程\end{cases} \Rightarrow \begin{cases}状态转换表\\状态转换图\\时序表\end{cases}\Rightarrow 逻辑功能 \]
- 驱动方程(激励方程): 触发器输入信号的逻辑表达式 \((如J_0=Q_1^n, K_0 = \overline{Q_0^n})\)
- 输出方程: 输出变量的函数 (Moore 型不包含输入 X, Mealy 型包含输入 X) (\(如Z=Q_1^n\overline{Q_0^n}\))
- 状态方程: 下一个状态的函数 (感觉更应该叫次态方程) \((如Q_0^{n+1} = J\overline{Q_0^n}+\overline{K}Q_0^n = Q_1^n\overline{Q_0^n} + \overline{Q_0^n}Q_0^n = Q_1^n\overline{Q_0^n})\)
- 分析一个时序电路, 就是找出给定时序电路的逻辑功能
- 找出电路的状态和输出在输入变量和时钟信号作用下的变化规律
- 可以用==输出方程== . 驱动方程 和 状态方程 求解出任何给定输入变量状态和存储电路状态下时序电路的==输出== 和==次态==
-
-
时序电路分析方法
- 确定系统变量 (输入变量, 输出变量, 状态变量)
- 列驱动方程(控制函数, 激励方程) , 列输出方程(输出函数) - 从逻辑(电路)图中写出每个触发器的驱动方程
- 列状态方程(次态函数) - 从得到的驱动方程代入触发器特征方程, 得到触发器状态方程, 进而求出电路==次态==
- 列状态转换表, 画状态转换图
- 画时序波形图(如有需要)
-
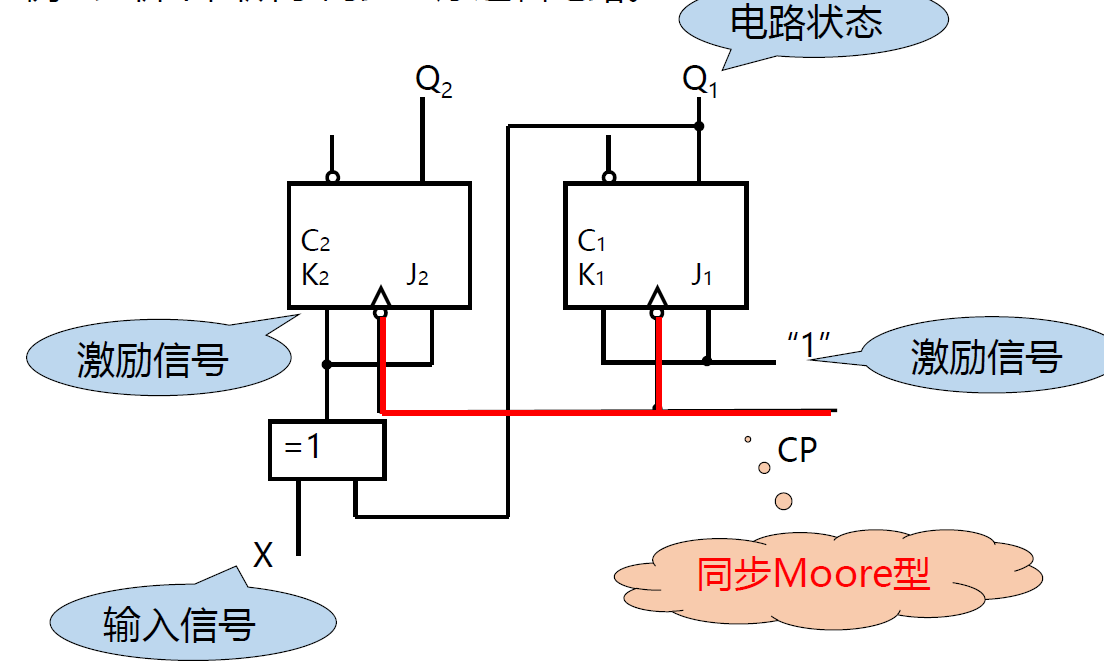
例 1: 分析 模四计数器(Moore)
-
逻辑方程式
- 输出函数表达式 : 单独的 y2, y1 (Moore 型) - 激励函数表达式 : \(\begin{cases}J_1 = K_1 = 1\\J_2 = K_2 = X\oplus y_1\end{cases}\) - 状态方程组 : \(JK触发器 : Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n\) - 代入得: \(\begin{cases}y_1^{n+1} = 1\cdot \overline{y_1^n} + \overline{1}\cdot y_1^n = \overline{y_1^n}\\ y_2^{n+1} = X\oplus y_2^n \oplus y_1^n\end{cases}\)
-
填状态转换表
- 现态次态状态转换表 & 真值表
<img src="数字电路与逻辑设计.assets\image-20221023001535502.png" alt="image-20221023001535502" style="zoom: 33%;" /> -
画状态转换图
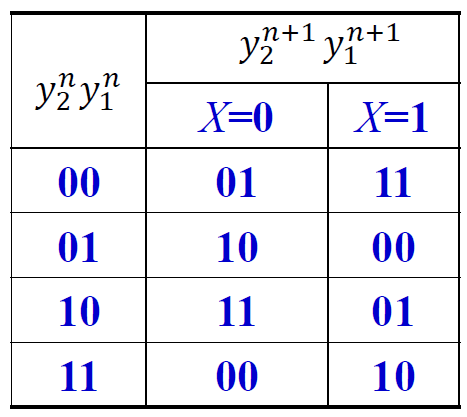
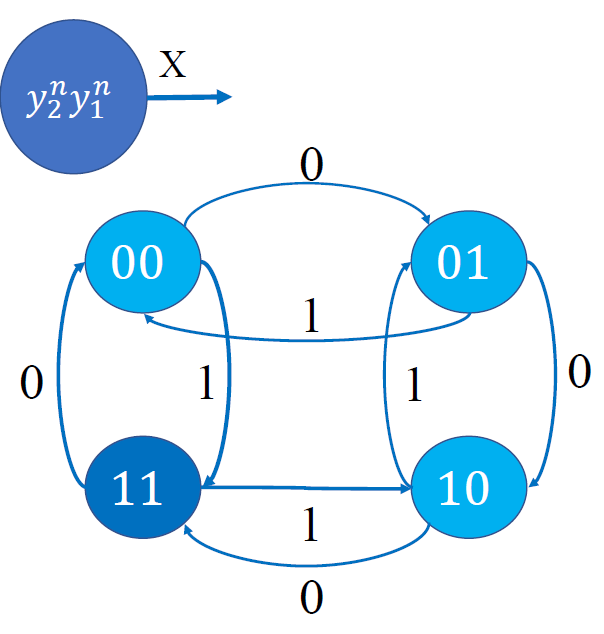
-
电路功能:
- X=0 时:
 电路进行模 4 加 1 计数
- X=1 时:
电路进行模 4 加 1 计数
- X=1 时:  电路进行模 4 减 1 运算
- 电路功能: 可你计数器, y2可以理解为进位 / 借位端 (加减的区别在于 初态是 00 时, 加减输出 1 的时刻不一样)
电路进行模 4 减 1 运算
- 电路功能: 可你计数器, y2可以理解为进位 / 借位端 (加减的区别在于 初态是 00 时, 加减输出 1 的时刻不一样) -
时序图
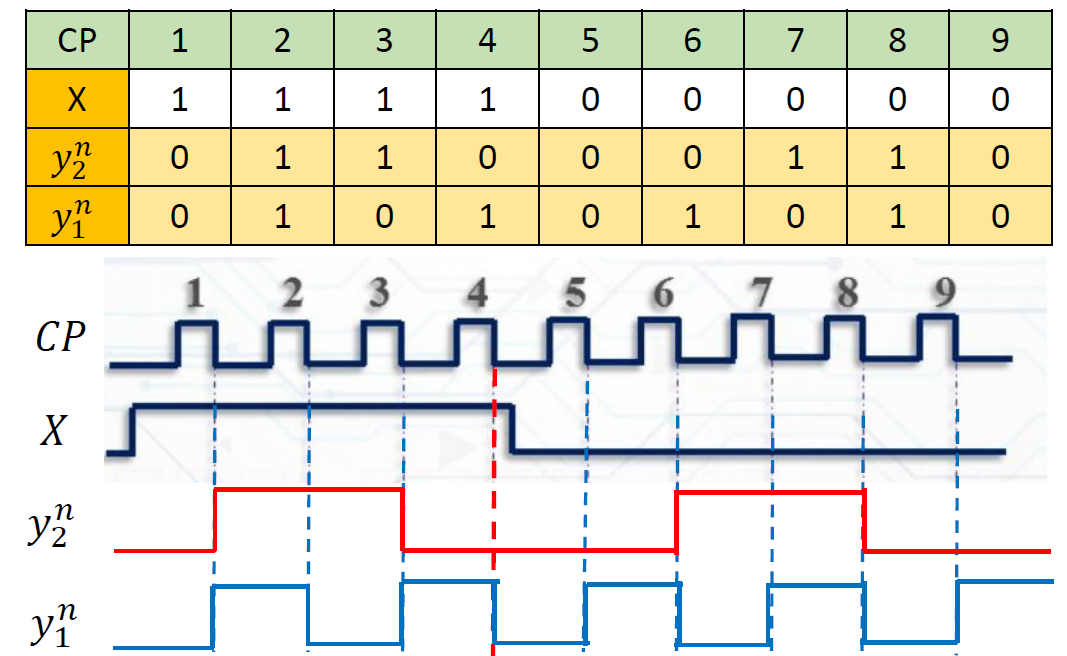
-
-
例 2 : 分析 模四计数器(Mealy)
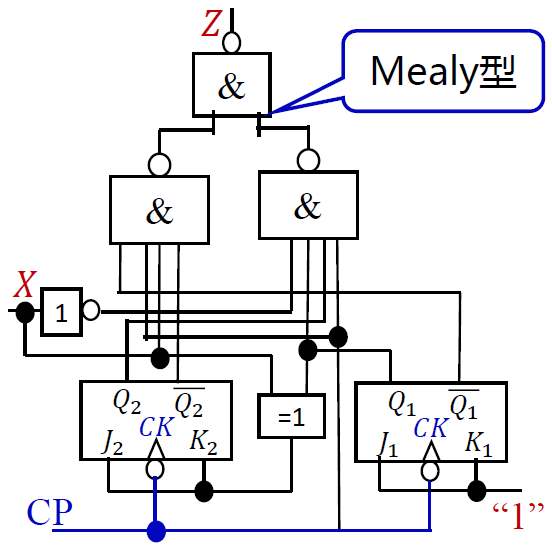

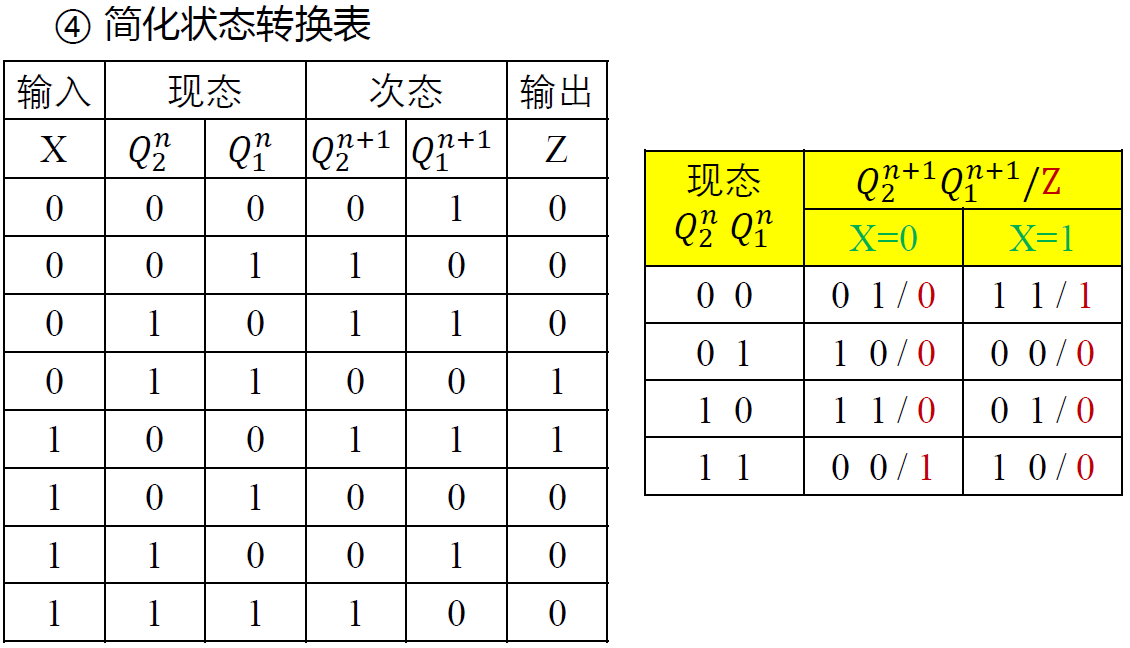
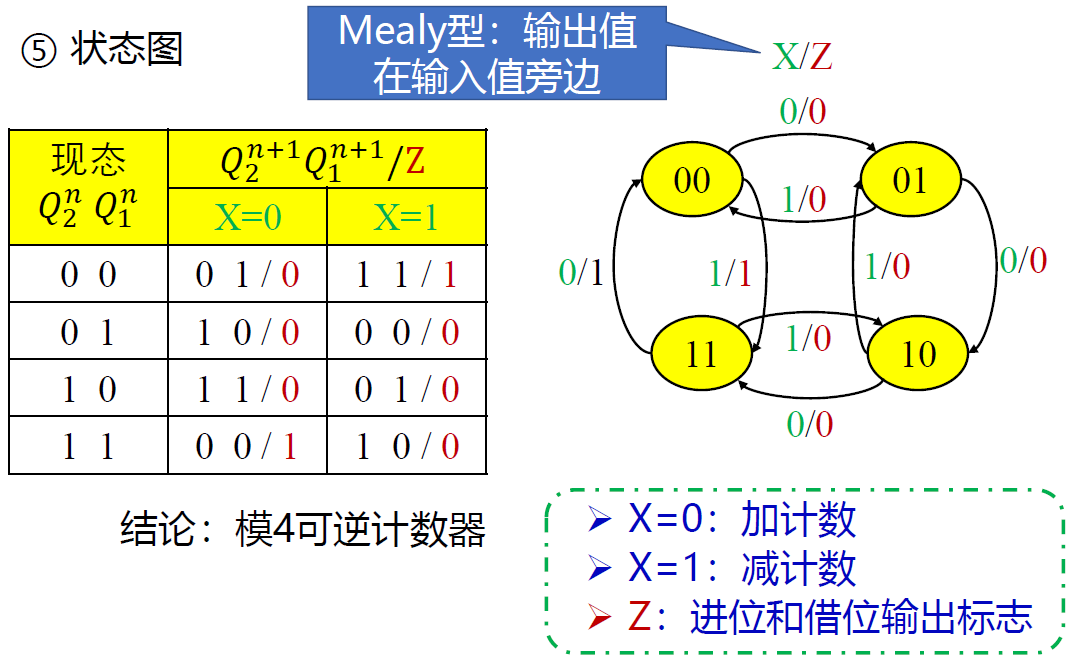
- Mealy 型同样可以实现 Moore 型的电路
-
例 3 分析 模八计数器
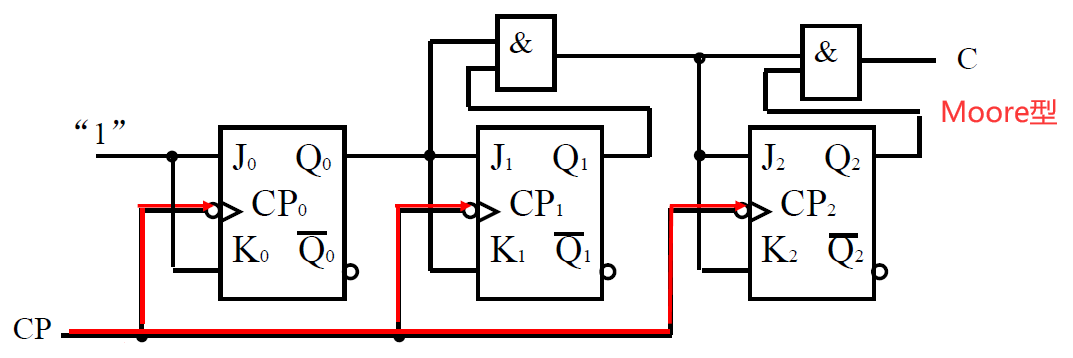
- ③ 输出方程 : \(C = Q_2Q_1Q_0\)
- ④ 状态表 :
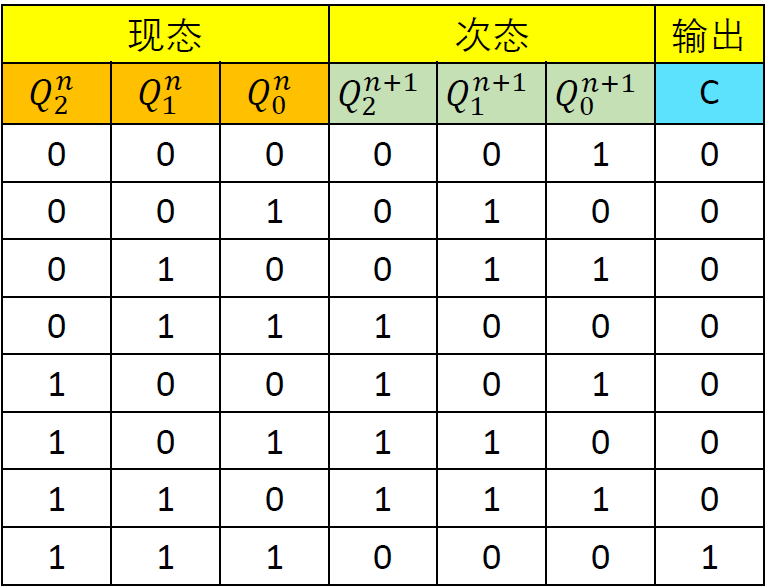 ⑤ 状态图 :
⑤ 状态图 : 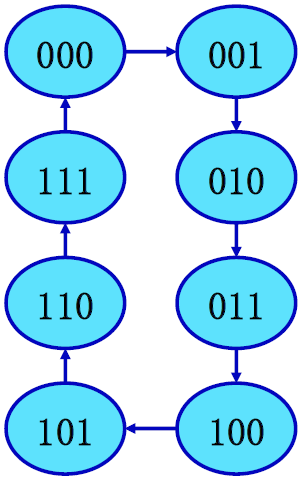
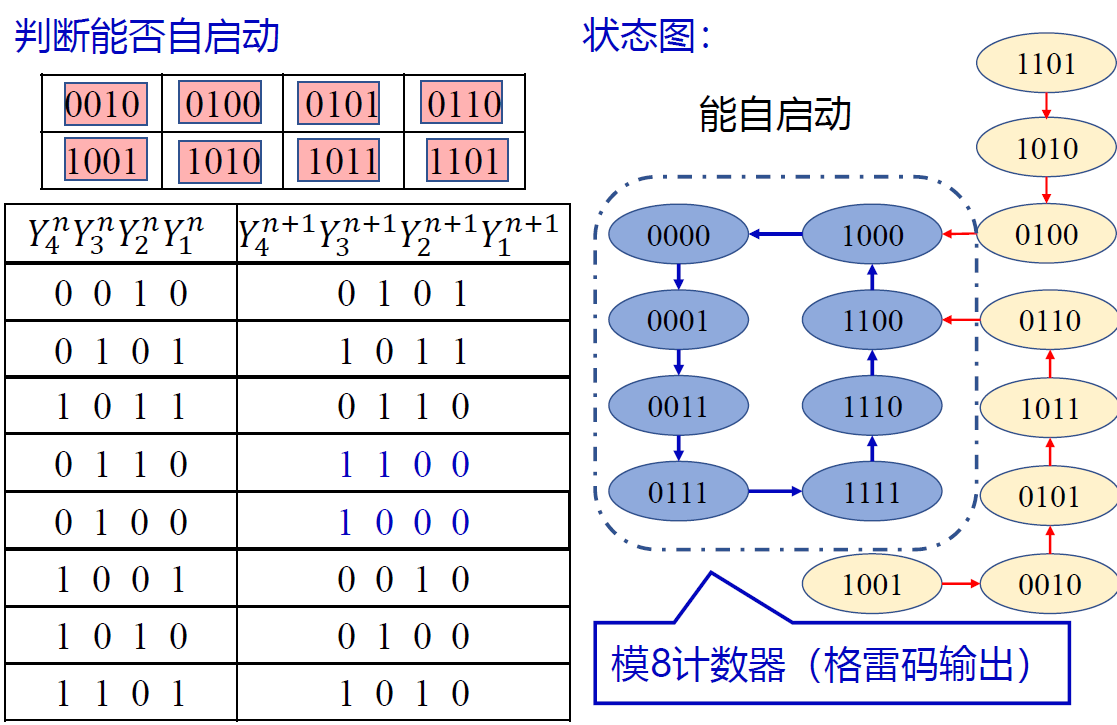
- 功能: 自启动 模八计数器
自启动 : 循环之外的状态如果能在时钟作用下进入循环
挂起 : 无法进入循环
-
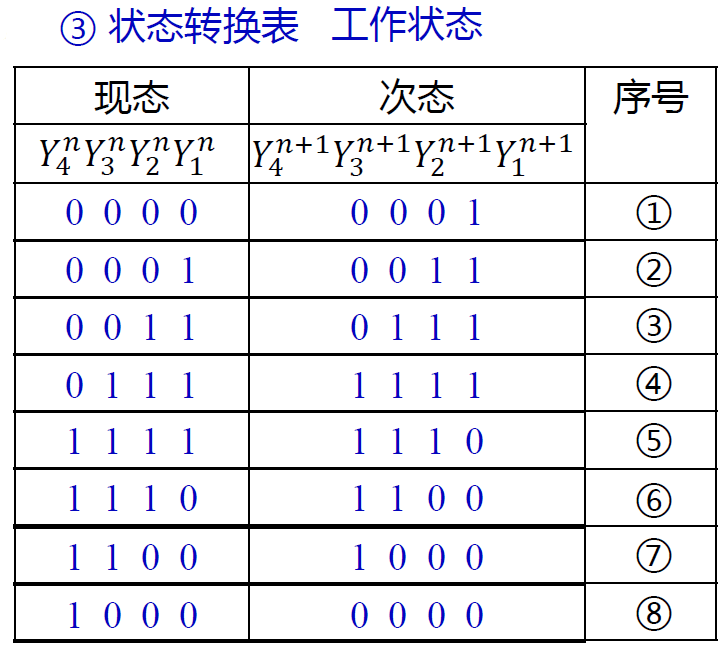
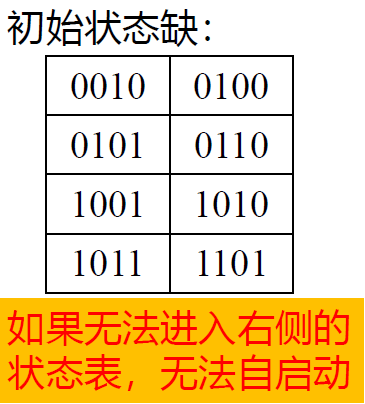
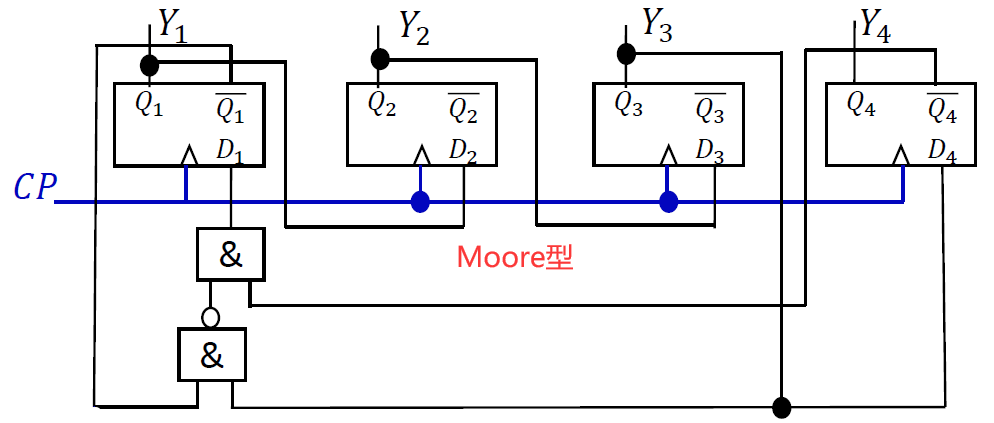
例 4 分析 模八计数器(格雷码输出)
-
例 5 分析 (可重复)1111 序列检测器
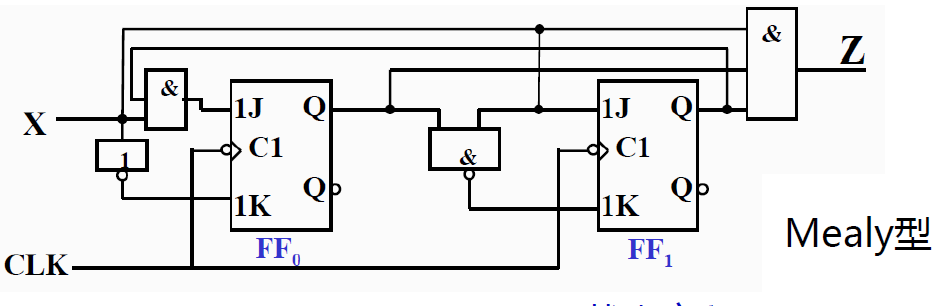

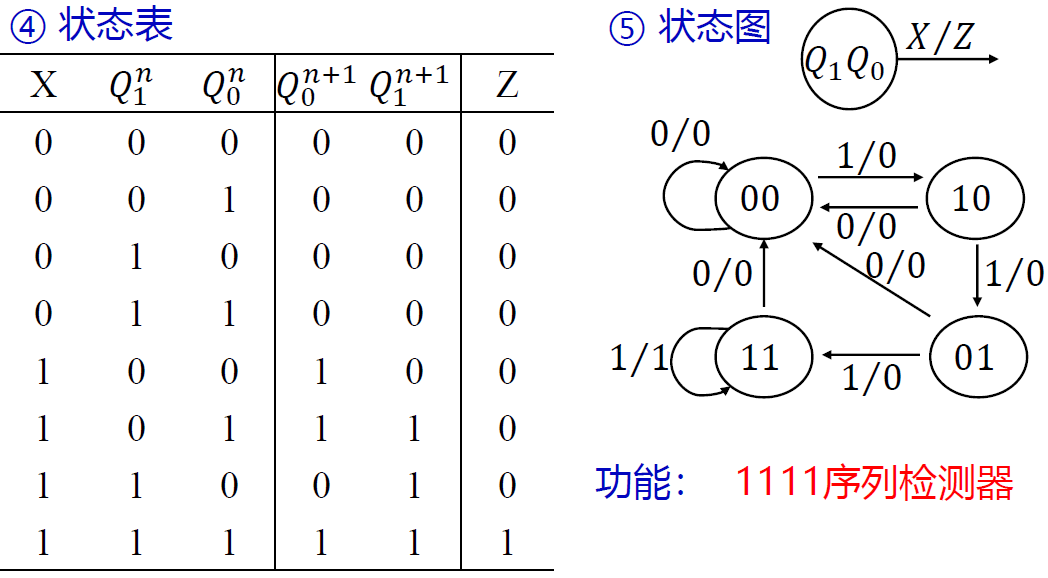
- 当且仅当连续输入 4 次"1"时, 才会输出 1
- 可重复: 继续输入 1, 状态保持不变
5.2.3 异步时序逻辑电路分析¶
-
异步时序逻辑电路分析的一般步骤
- 写出 时钟方程 . 输出函数 和 驱动方程
- 将 驱动方程 代入触发器的 特性方程 ,得到各个触发器的 状态方程
- 建立 次态真值表(状态转移表),表中加一列时钟信号的变化,画出 状态图
- 说明电路的逻辑功能,判断电路 有无自启动能力 (挂起现象的讨论)
- 异步和同步的区别仅在于 时钟 , 也就是在同步的基础上 分析什么时候状态会改变
-
例 1 分析异步 异步模 4 加 1 计数器
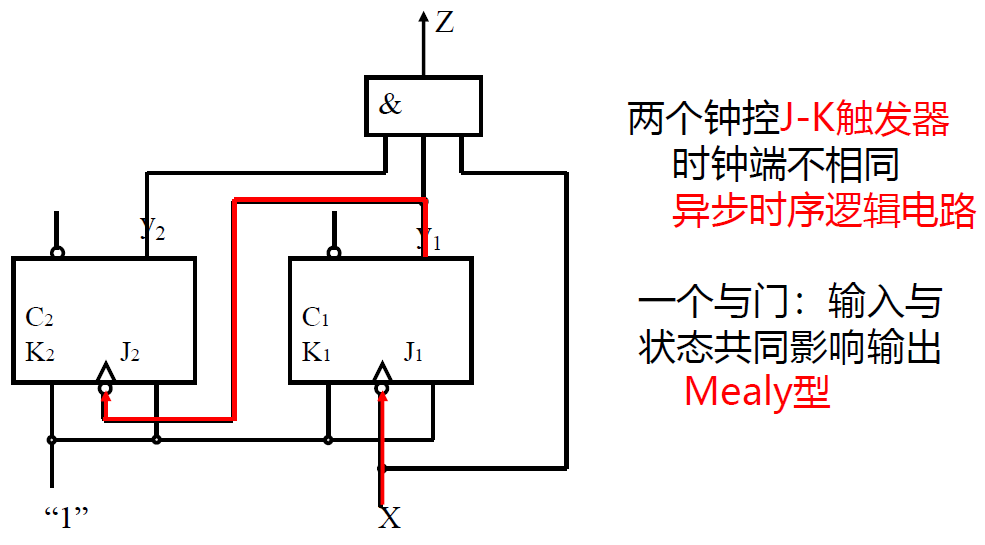
- 驱动函数表达式 : \(J_1 = K_1=1; J_2 = K_2=1\)
- 时钟方程 : \(CP_1 = X; CP_2 = y_1\)
- 状态方程 : \(y_2^{n+1} = \overline{y_2^n};\quad y_1^{n+1} = \overline{y_1^n}\)
- 状态转移表 :
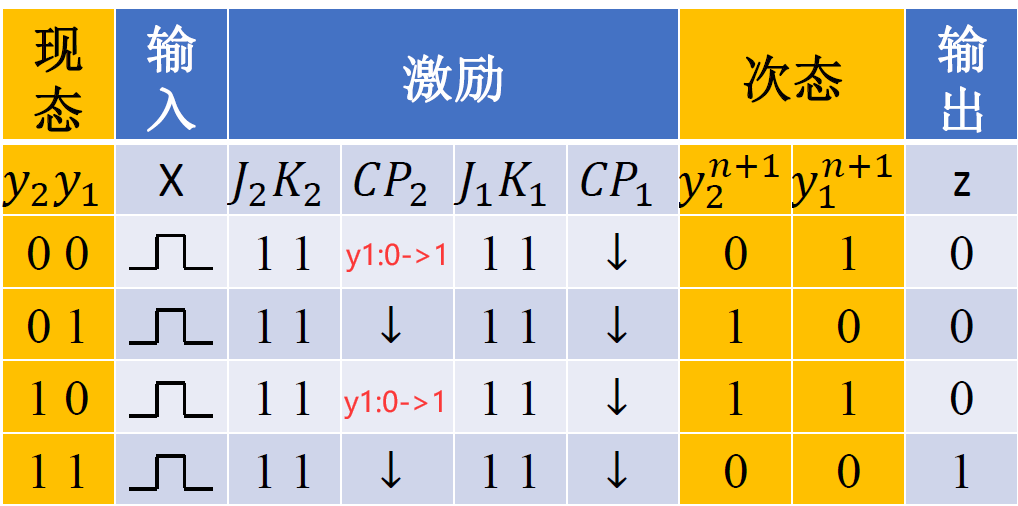
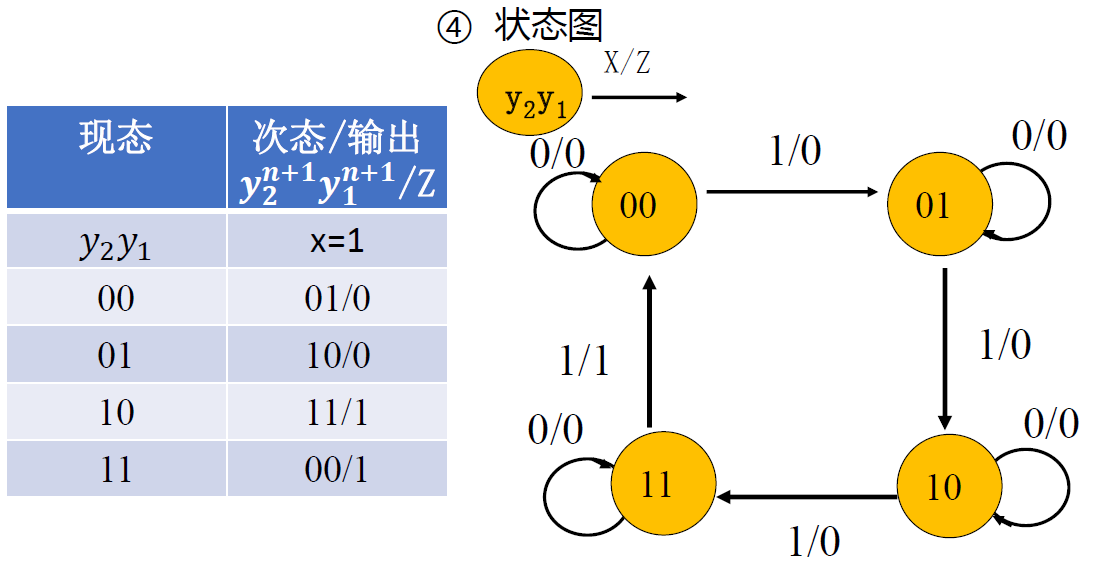
- 异步模 4 (两位二进制. 四进制. 四状态)加 1 计数器,当收到第四个输入脉冲时,电路产生一个进位输出脉冲; 当 X=0 时,电路保持不变;
-
计数/分频功能
-
脉冲信号: 是按一定电压幅度,一定时间间隔连续发出。
- 脉冲信号之间的时间间隔称为周期 T - 在单位时间(如 1 秒)内所产生的脉冲个数称为 频率 f
-
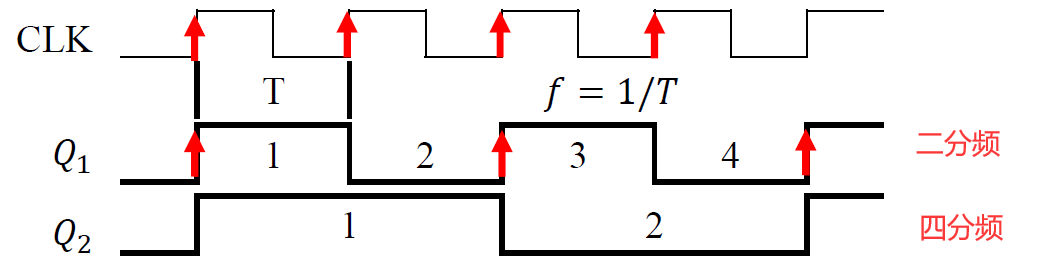
- 计数器 : 顾名思义就是在时钟的节拍下进行计数。 - 计数器在某种意义上讲,等同于对时钟进行分频。 - 分频 : 是指将意单一频率信号的频率降低为原来的 1/N
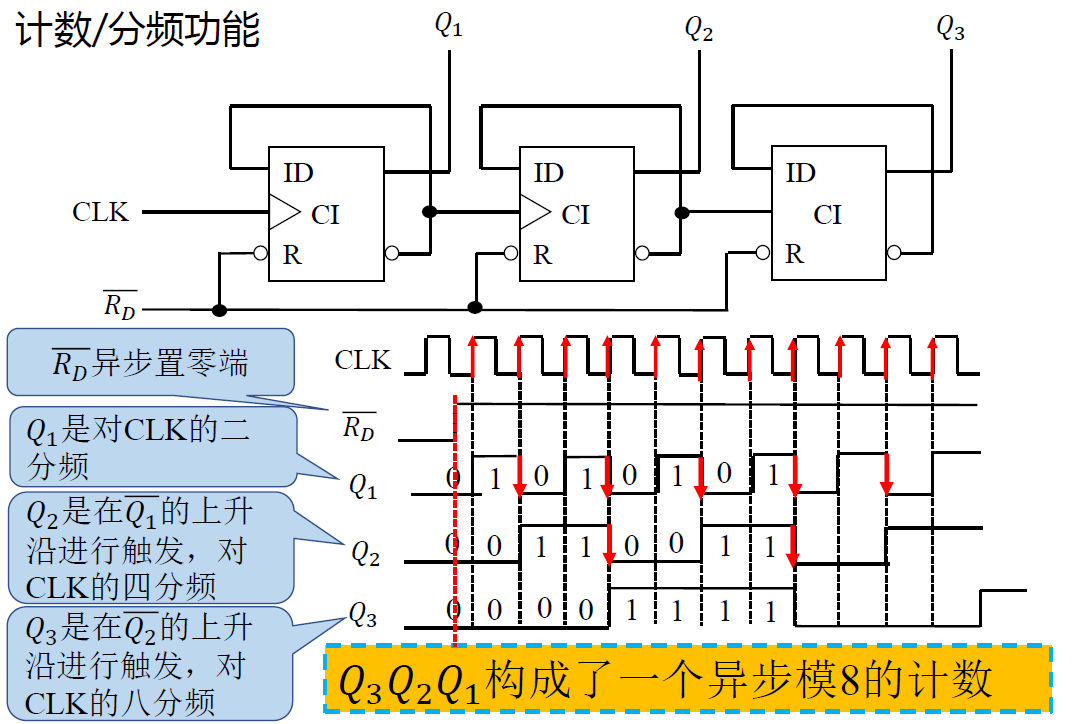
-
5.3 同步时序逻辑电路设计¶
5.3.1 触发器设计同步时序逻辑电路步骤¶
- 根据需求 → 形成原始状态图和原始状态表
- 状态化简, 求出最简状态图 状态表
- 状态编码, 得出二进制状态表
- 状态转移表 + 触发器特征方程 → 触发器激励
- 卡诺图化简 → 激励(输入)函数表达式 + 输出函数表达式
- 画出逻辑电路图
- 检查无关项
- 公式法 : \(状态方程 + 触发器的特性方程 \overset{观察}{\Longrightarrow} 激励方程\)
- 表格法 : $状态表 + 触发器的真值表 \stackrel{卡诺图化简}{\Longrightarrow} 激励方程\textcolor{orange}{(根据表格画出针对如 J_1 K_1 J_2 K_2 等卡诺图, 然后化简获得激励方程)} $
- 表格法一定能算出来, 但是比较麻烦; 公式法对于一些公式可能不好观察
例_公式法_13 进制计数器¶
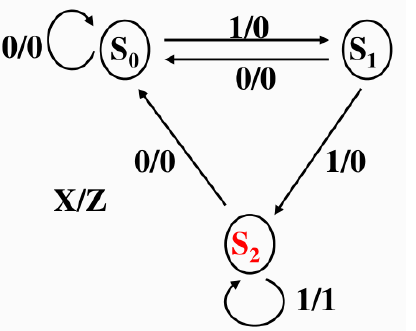
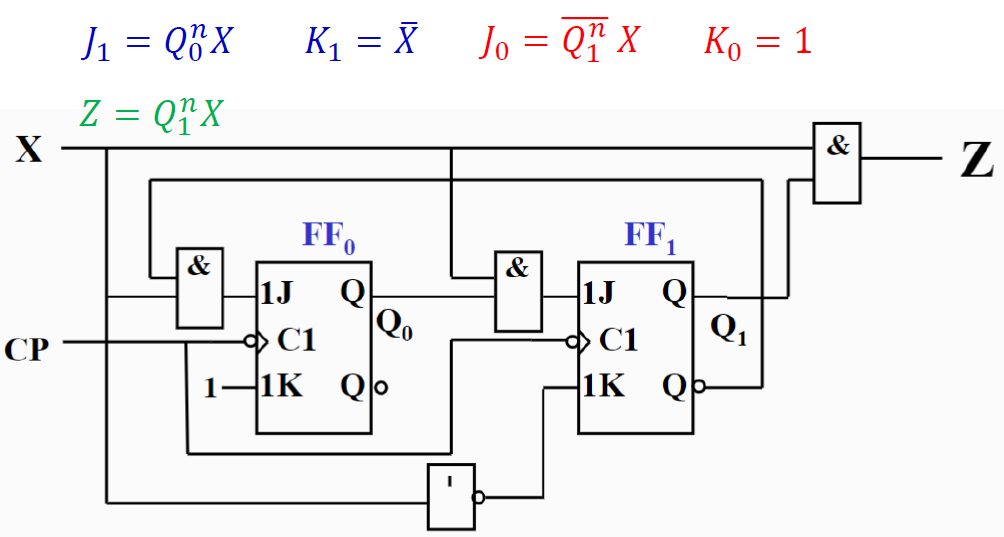
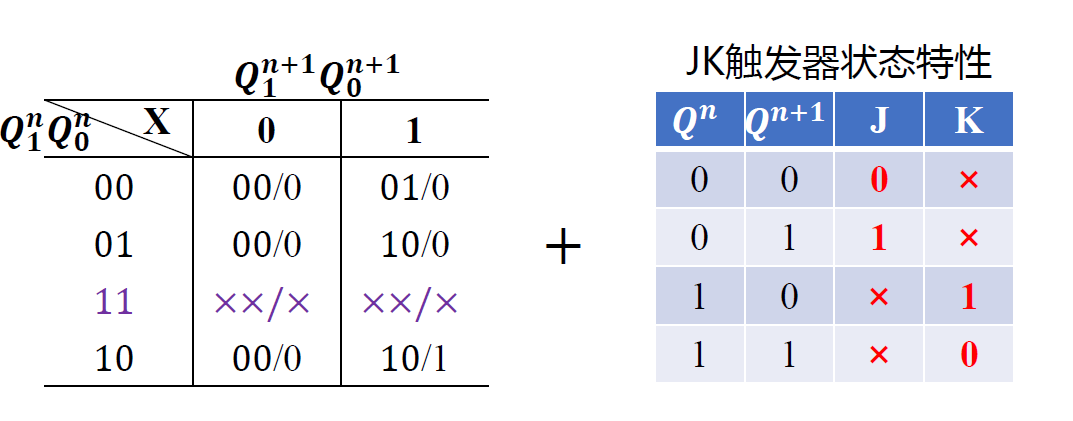
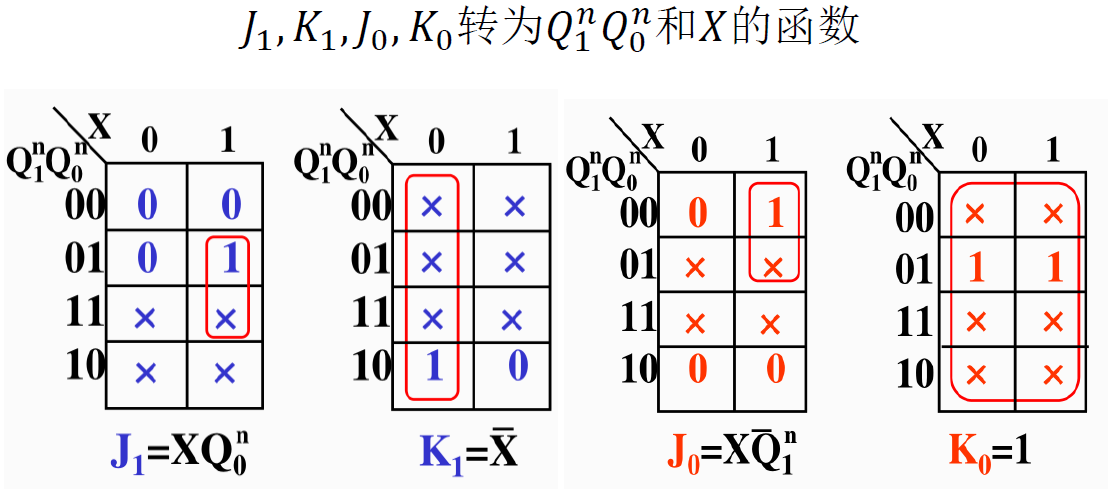
例 : 用触发器设计一个带有进位输出端的十三进制计数器 (公式法, 对次态进行讨论)
-
确定输入输出变量 : 由于电路没有输入变量,故属于 Moore 型同步时序电路。设进位输出信号为 C ,有进位输出则 C=1 ,无进位输出时 C=0.
-
给出状态转换图:根据题意,M=13,其状态由 13 个状态构成,以 𝑆𝑖表示
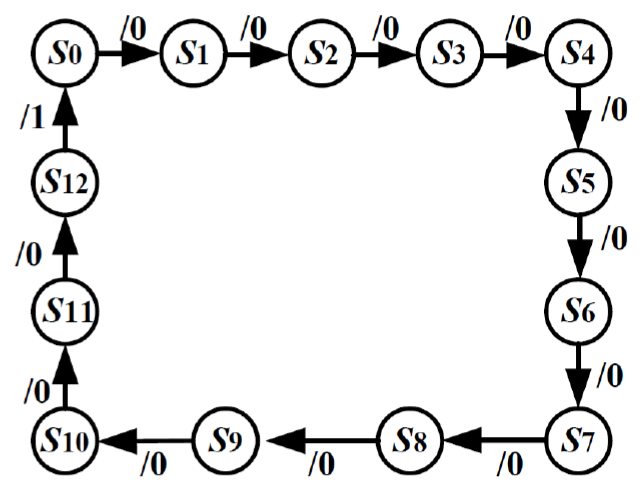
-
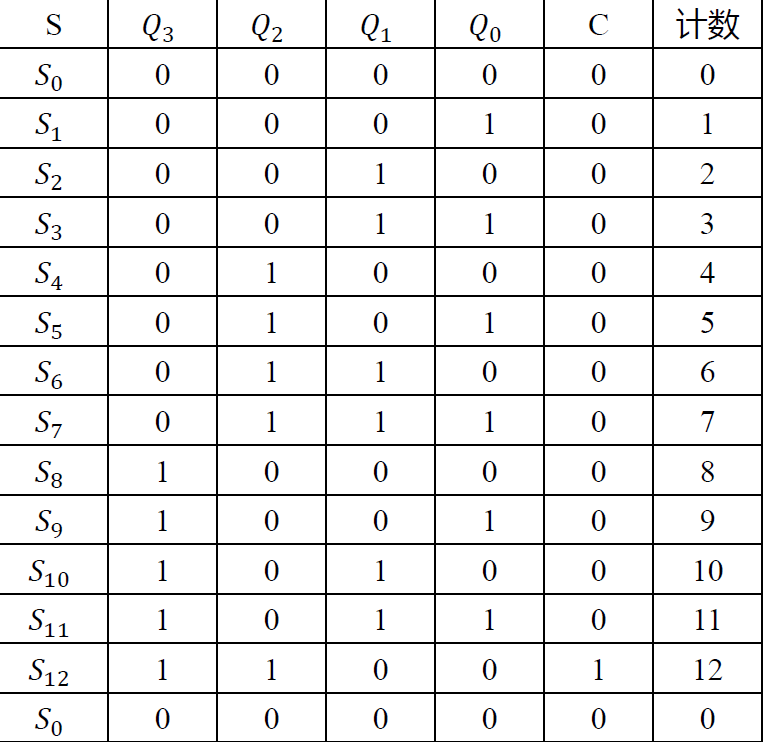
给出状态表 : M=13 > 23, 需要四位子长编码, 共 16 个状态, 取其中的 13 个状态(0-12)使用
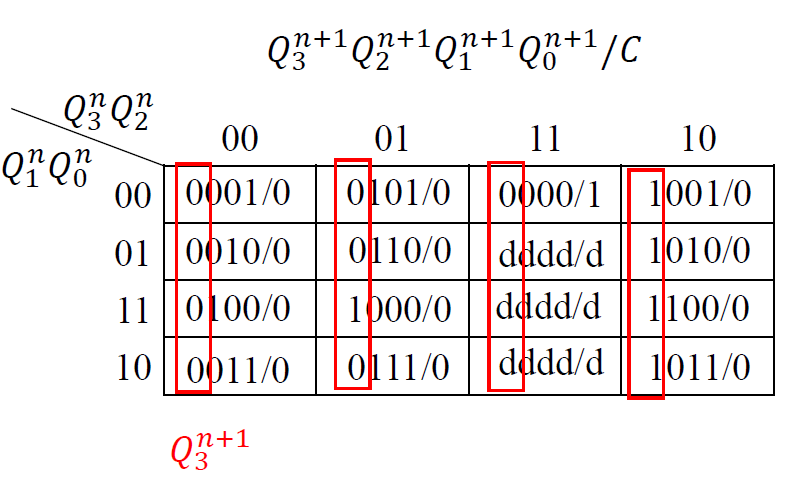
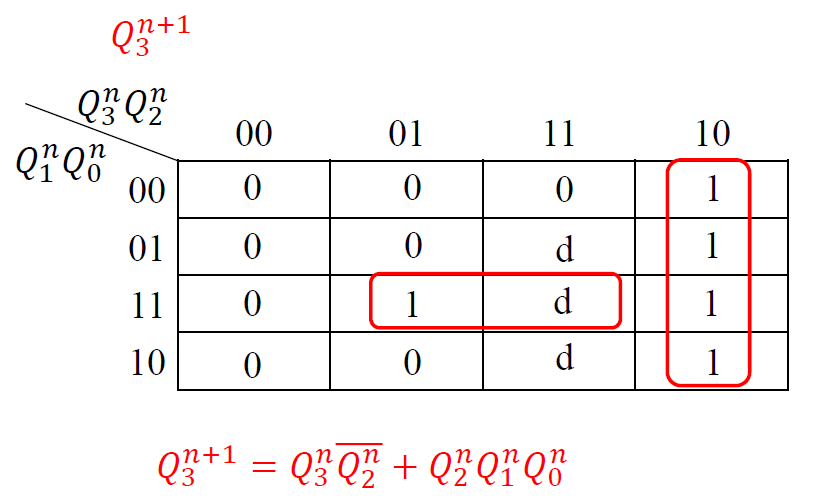
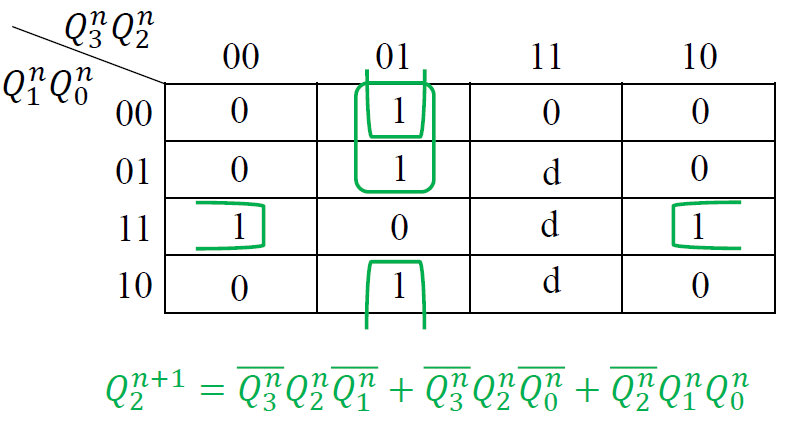
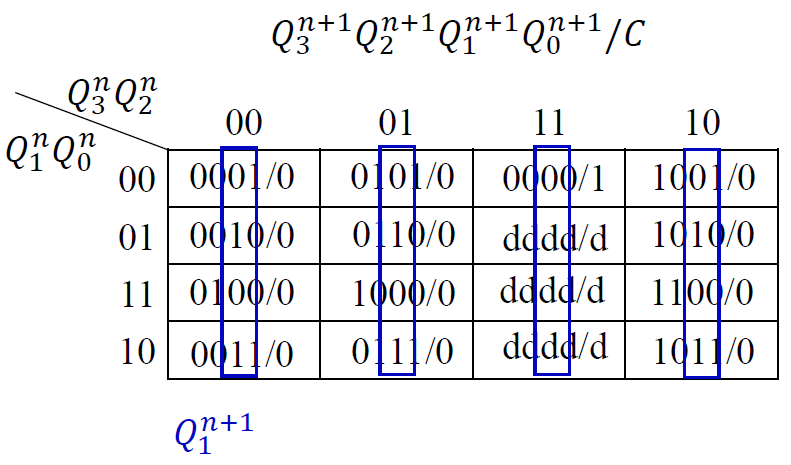
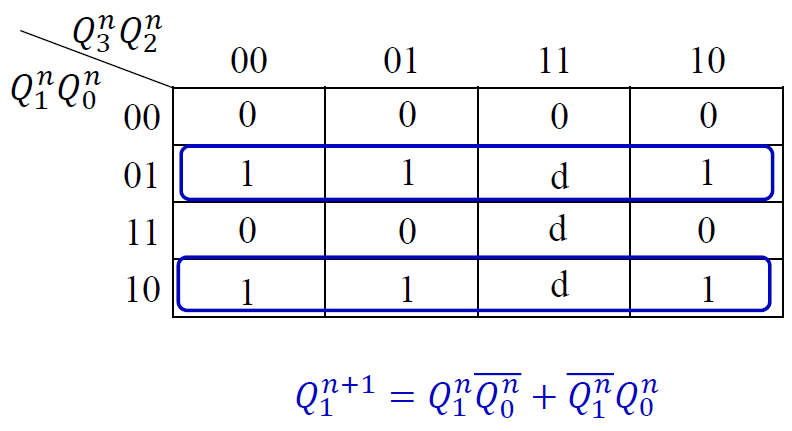
画出各输出端的卡诺图: 根据状态表得出各个输出次态的卡诺图



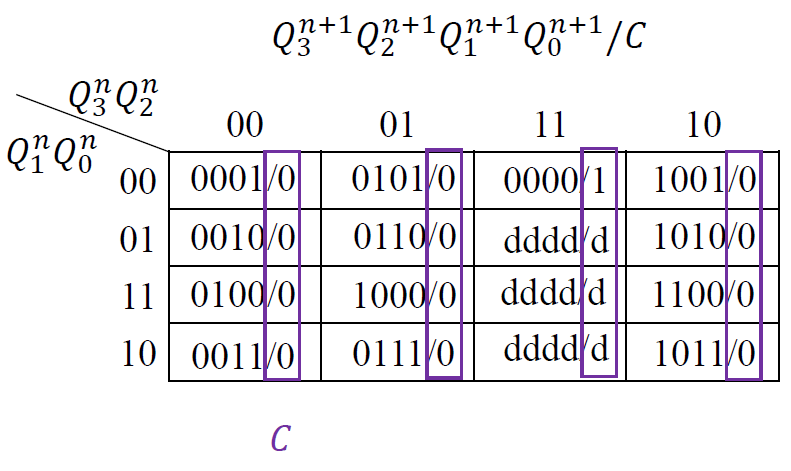
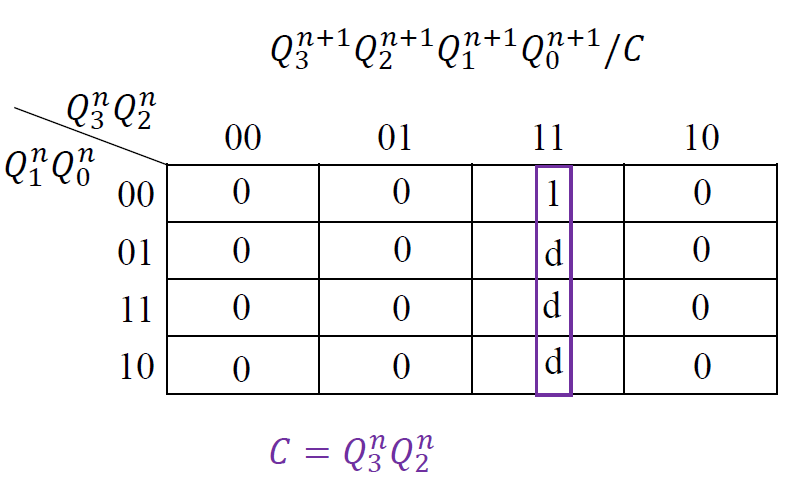
-
-
写出电路的状态方程和输出方程
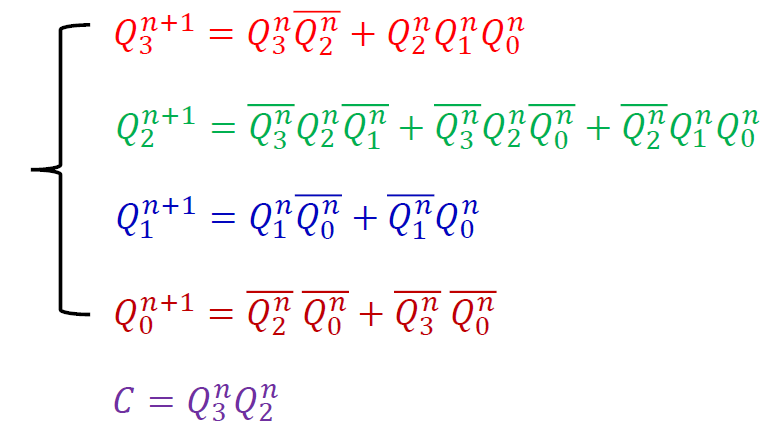
-
选择 JK 触发器来实现 (\(Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n\))
把上述方程转为 JK 触发器特性方程标准形式,可得激励信号
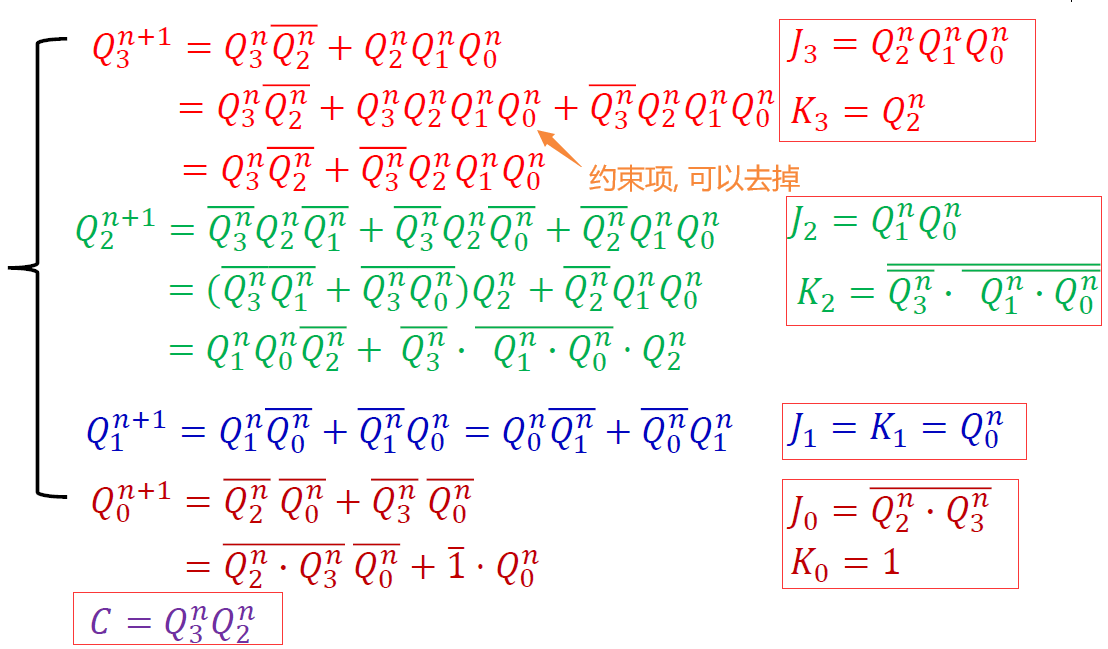
-
-
-
-
画电路图:根据驱动方程画出十三进制计数器的逻辑电路
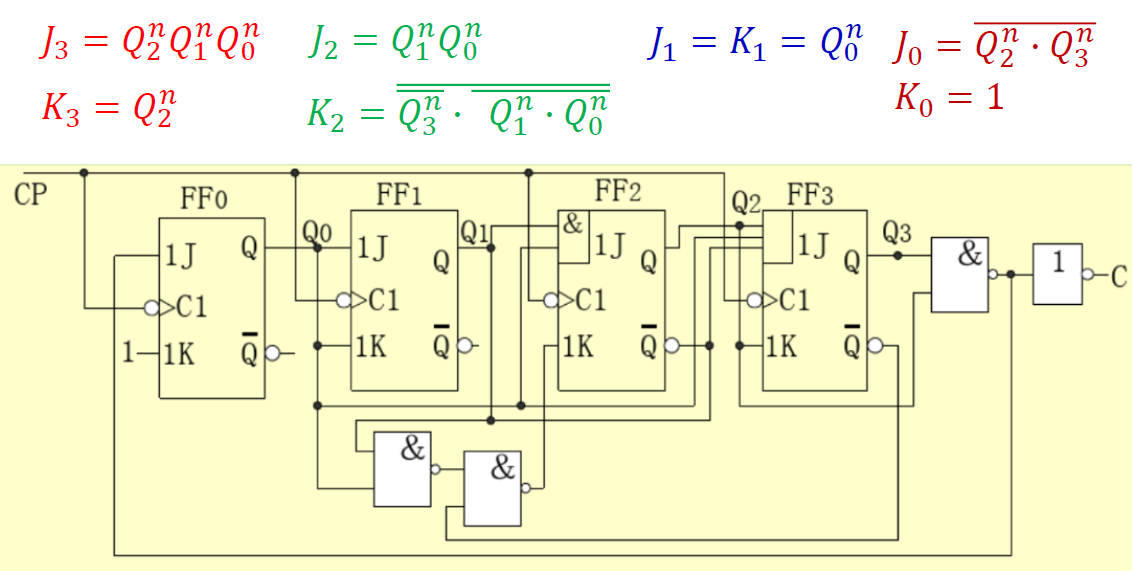
-
检查电路能否自启动 : 讨论全部情况(约束项同样需要考虑进去)
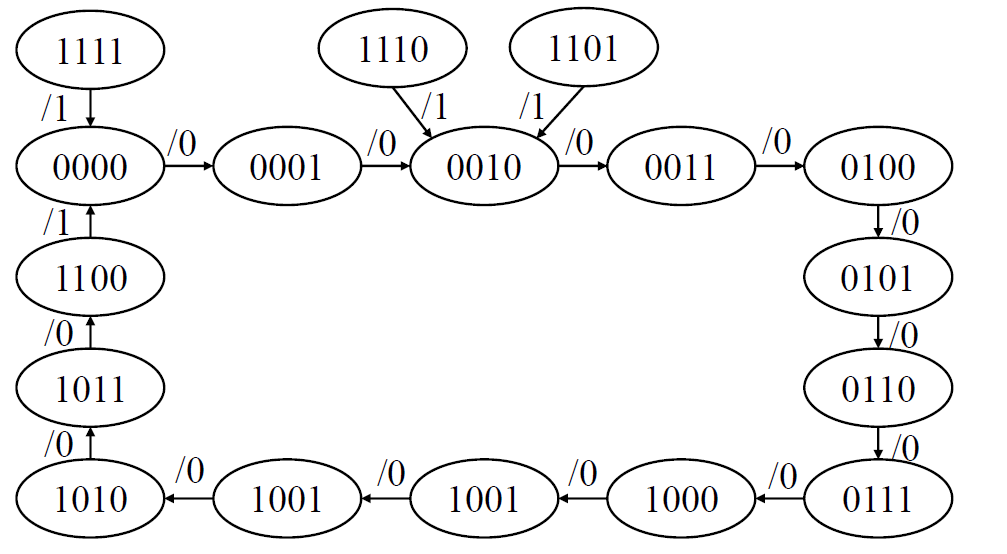
电路可以自启动
例_公式法_序列检测器¶
序列检测器(公式法) : 试设计一个“ 111 ”序列检测器。
要求 : 当连续输入 三个或三个 以上“1”时输出为“1”,否则输出为 0
-
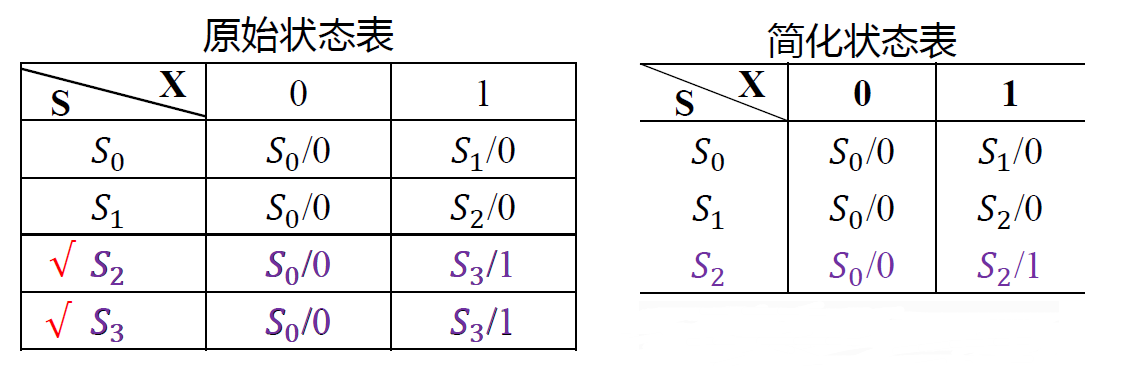
建立原始状态图, 原始状态表
- S0:输入 0 以后的状态(即未收到一个“ 1 ”以前的状态)
- S1:输入一个"1"以后的状态
- S2:连续输入两个"1"以后的状态
- S3:连续输入三个或三个以上"1"以后的状态
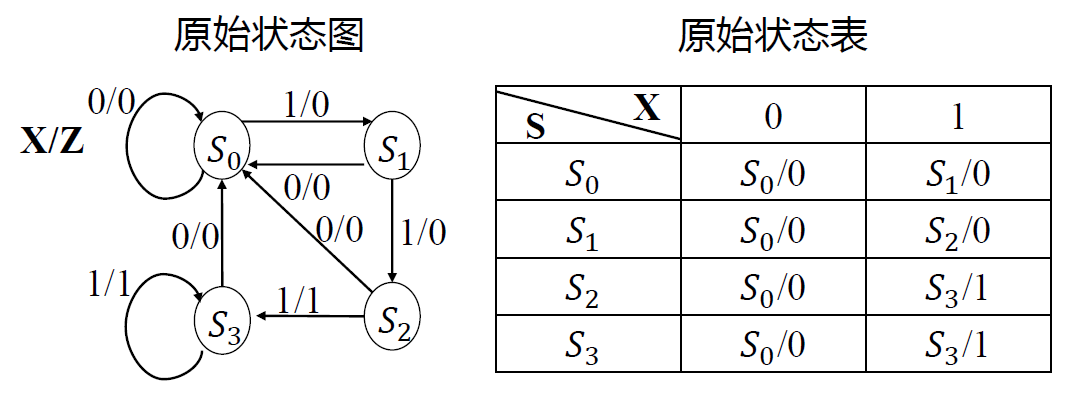
-
状态化简
-
状态 S2和 S3在相同的输入下有相同的输出,而次态也相同,称 S2和 S3两个状态等价 。
等价状态仅需保留一个。这里,去除 S3 ,保留 S2可得简化状态图。
-
状态编码
- 3 个状态, 需要两个触发器, 每个状态用 2 进制编码
- S0 : 00 S1 : 01 S2 : 10

-
驱动方程
- 选择 JK 触发器, 求出\(J_1, K_1, J_0, K_0, Z\)
- 1.
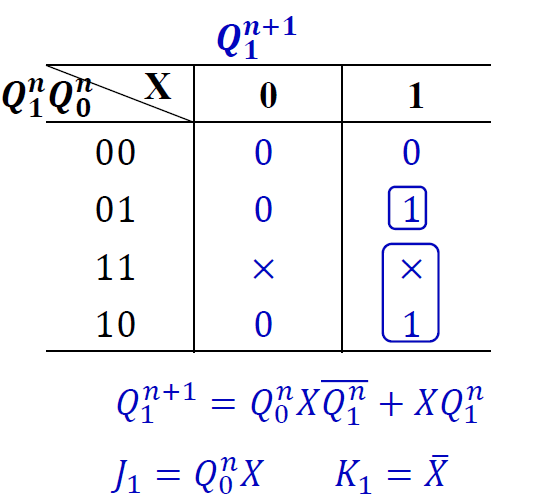 2.
2.  3.
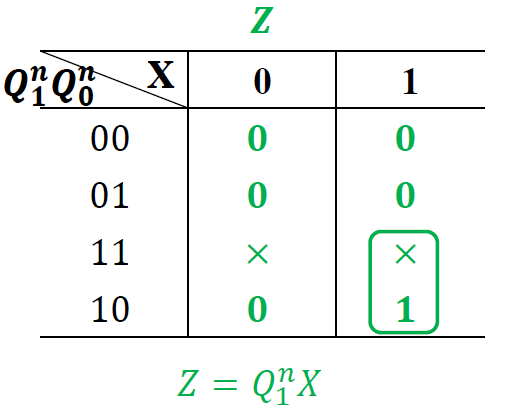
3. 
-
画电路图
-
检查自启动特性 -- 主要检查无效状态
5.3.2 [状态化简]¶
- 两种方法 : 目测法(肉眼可得)和隐含表法
-
目测法
-
输出相同, 次态相同
-
输出相同, 次态交错
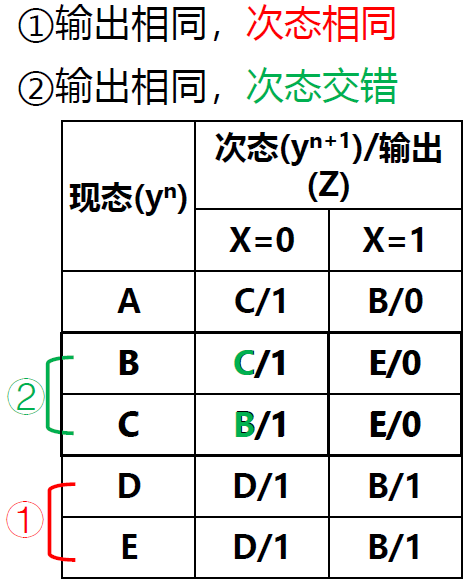
-
输出相同, 次态循环
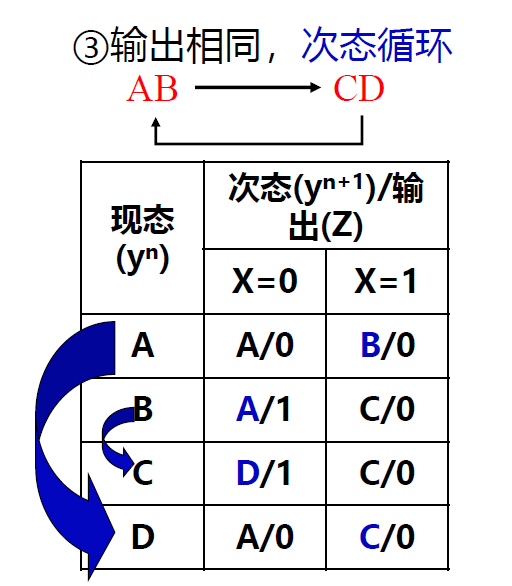
输出相同
BC 是否等价取决于 AD
AD 是否等价又取决于 BC, 次态循环
-
-
隐含表法
- 构成隐含表(横去尾,纵去头)
- 顺序比较:比较结果做 3 种记号“ ✓ ”. “×”. 状态对)
- 关连比较
- 形成最大等效类
- 合并化简
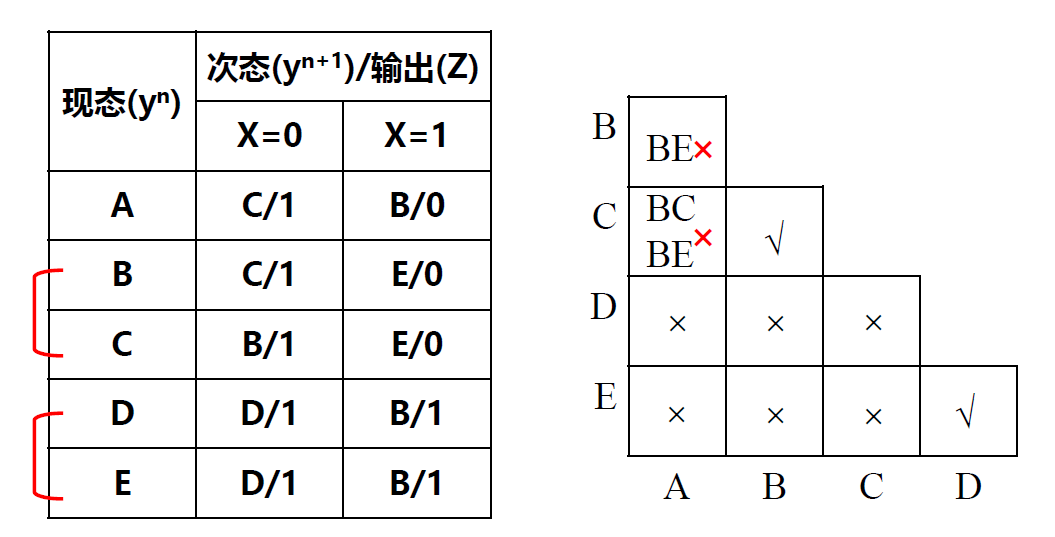 行没有 A, 列没有 E
行没有 A, 列没有 E
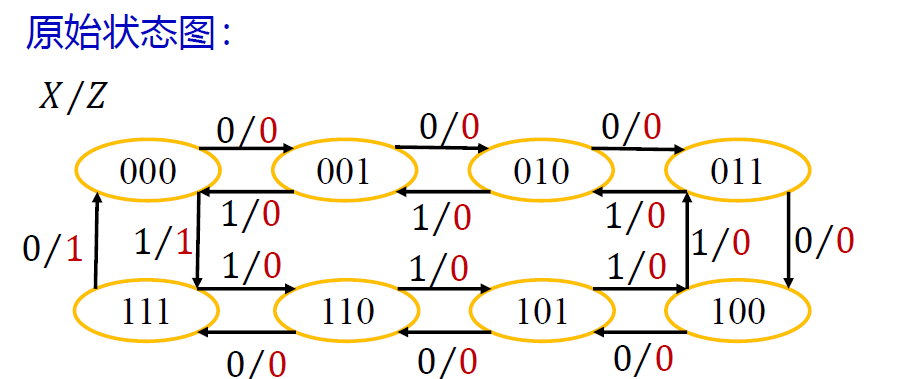
例_表格法_模 8 可逆计数器¶
例 3 计数器 : 利用 T 触发器设计一个同步模 8 可逆计数器 (表格法, 对触发器状态进行讨论)
-
8 个状态, 需要 3 个 T 触发器, 状态编码从 000~111 共 8 个状态。选择 Mealy 型,输出作为进位和借位标志
-
状态转换表 通过状态
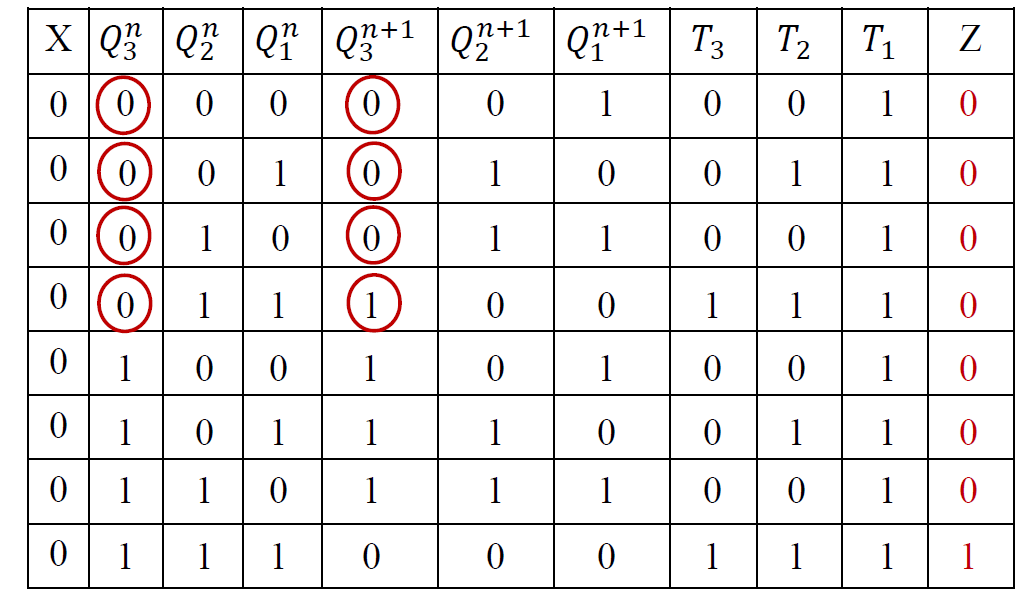
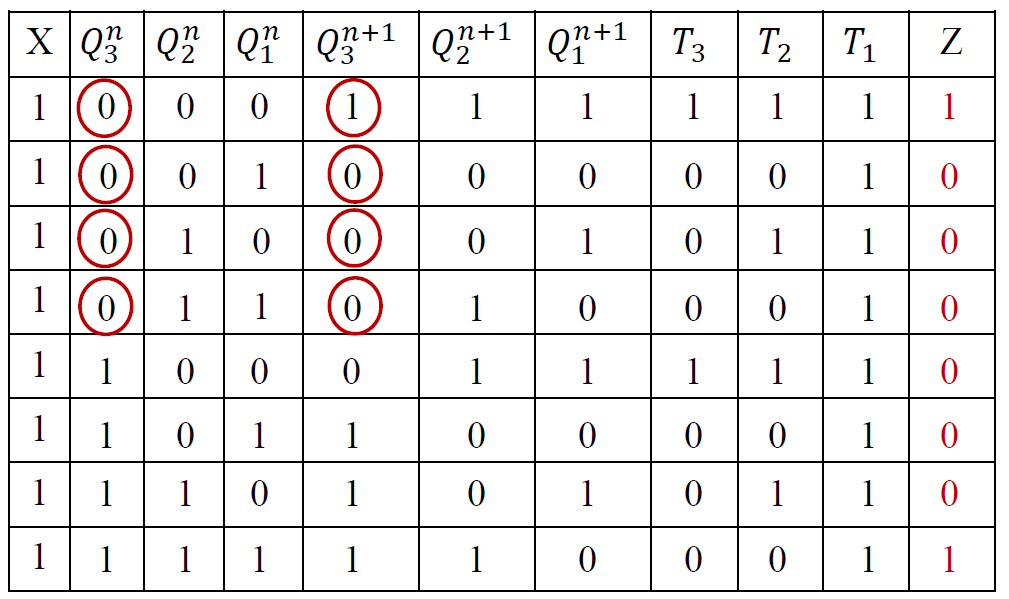
T1 = 1
-
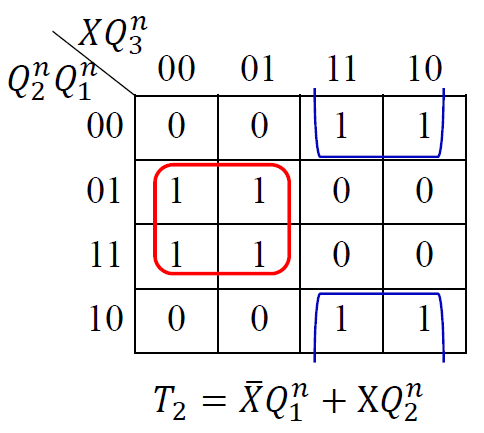
卡诺图化简, 得到激励方程


-
画电路图
-
求驱动方程的两种方法
公式法 表格法 ① 状态转移表(根据设计需求)
② 写出次态方程(\(如Q_1^{n+1} = Q_1^n\oplus Q_2^n\)) (使用卡诺图分析化简)
③ 结合触发器的特性方程(\(如JK:Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n\)) 得到驱动方程① 状态转移表(根据设计需求)
② 结合触发器的输入表(激励表) 画出包含触发器输入变量的表格
③ 使用卡诺图分析化简, 得到驱动方程-
触发器的输入表:
-
例_表格法_111 序列检测器¶
-
序列检测器(表格法) : 试设计一个“ 111 ”序列检测器。要求 : 当连续输入 三个或三个 以上“1”时输出为“1”,否则输出为 0
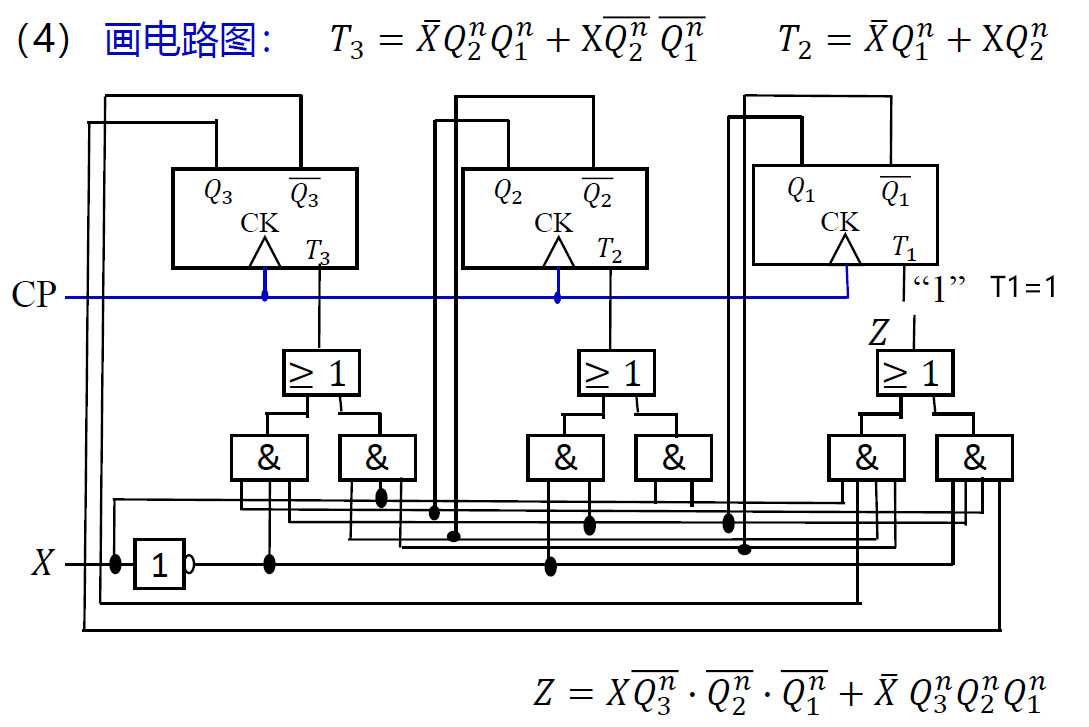
例_公式法_110 序列检测器¶
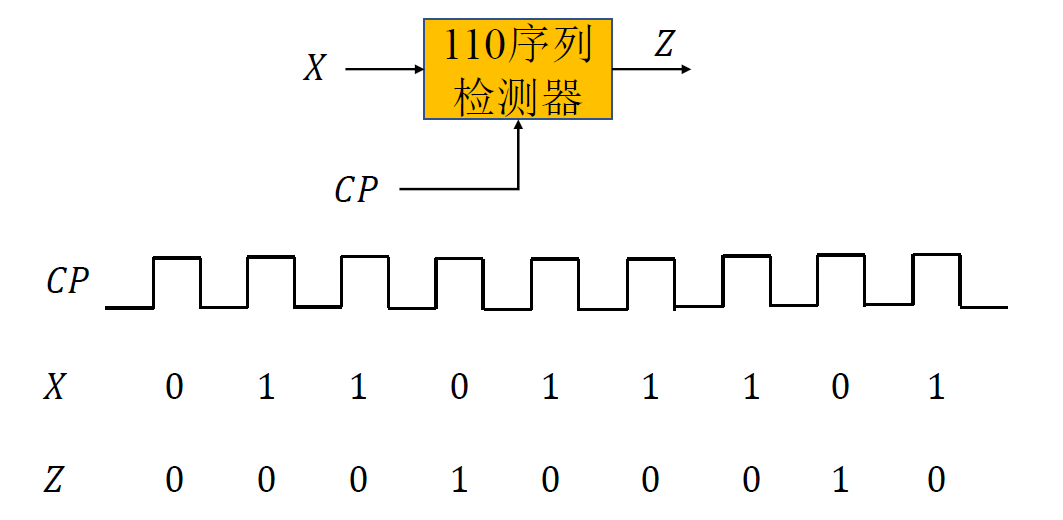
序列检测器: 利用 JK 触发器设计“ 110 ”序列检测器。
-
状态数: 4; 使用 Mealy 型电路
𝑆0——初始状态,表示收到 1 位数据: 0 𝑆1——表示收到 1 位数据 : 1 𝑆2——表示收到 2 位数据 : 11 𝑆3——表示收到 3 位数据 : 110 ,此时输出标志 Z=1
-
分析状态变化:
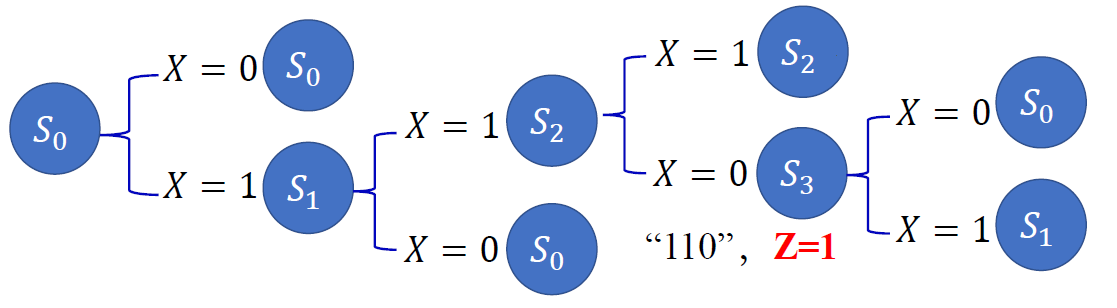
-
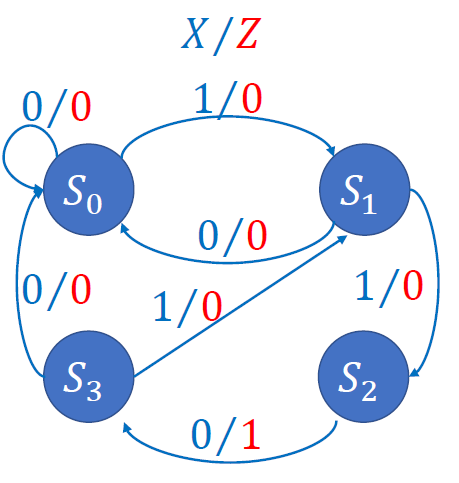
原始状态图:
-
原始状态表:
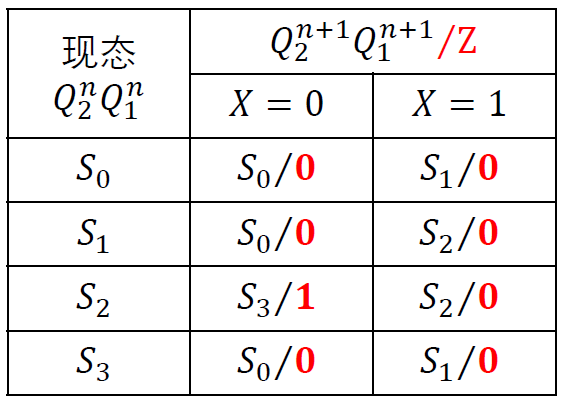
-
化简状态表:
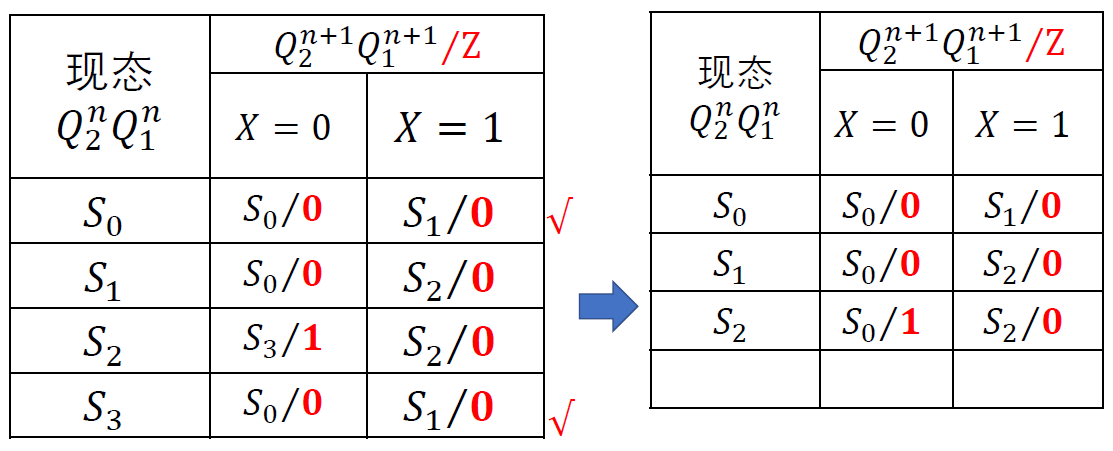
-
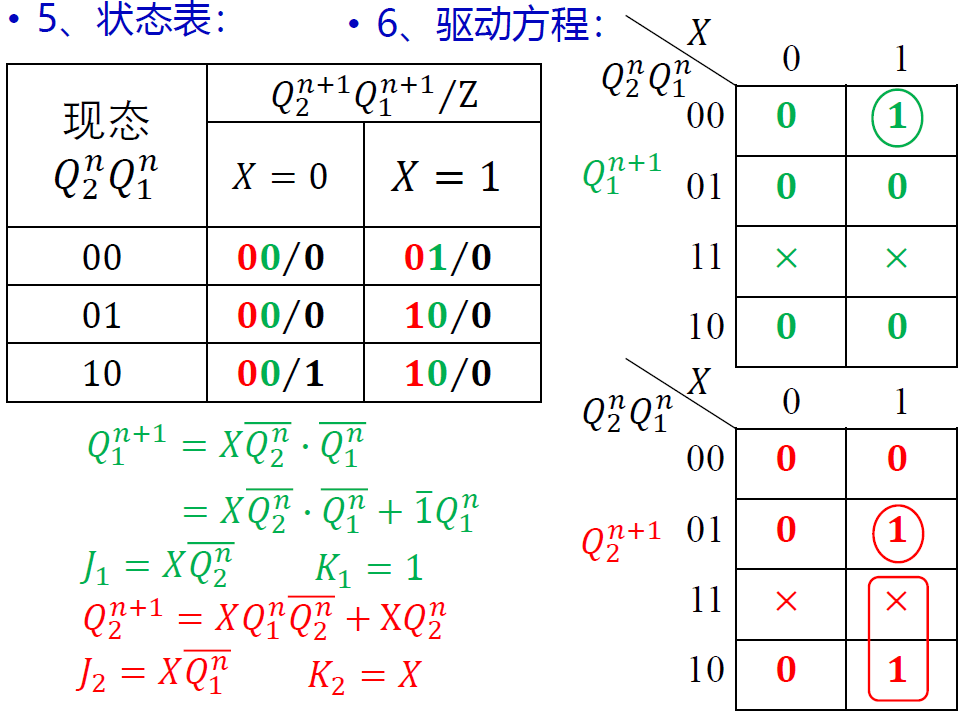
状态编码: 𝑆0——00; 𝑆1——01; 𝑆2——10
-
状态表 & 状态方程 => 驱动方程:
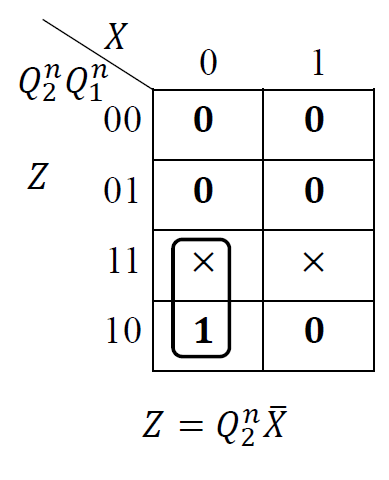
-
画逻辑电路图
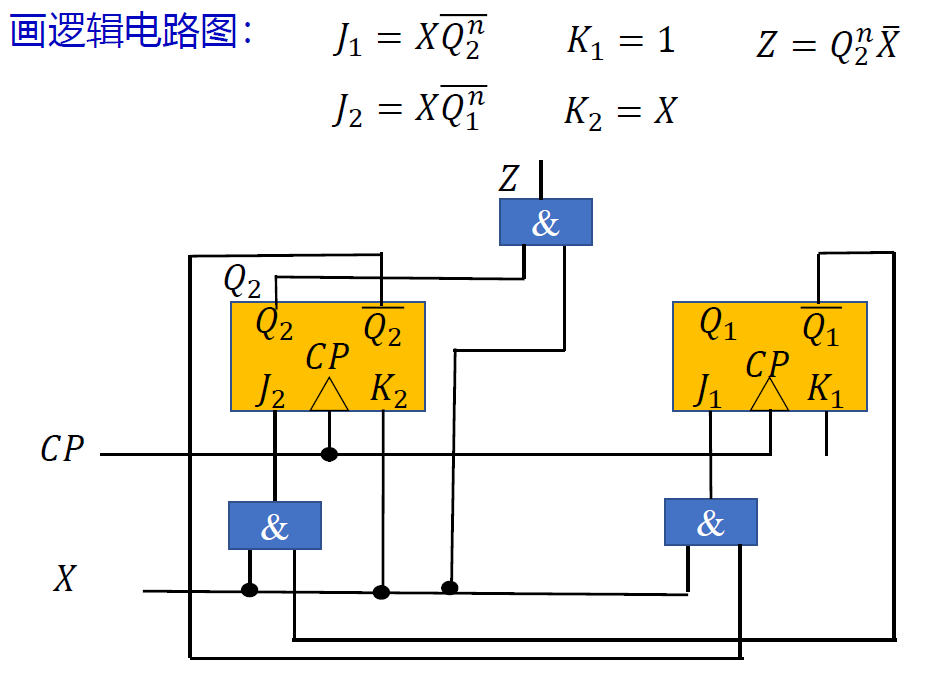
-
检查电路的自启动功能:
- 在设计线路的过程中, 现态 11 被化简, 现在需要重新考虑
- 状态方程: \(\begin{cases}𝑄_1^{𝑛+1}=𝑋\overline{𝑄_2^𝑛}\cdot\overline{𝑄_1^𝑛}\\𝑄_2^{𝑛+1}=𝑋𝑄_1^𝑛\overline{𝑄_2^𝑛}+X𝑄_2^𝑛\\𝑍=𝑄_2^𝑛\overline{ 𝑋}\end{cases}\)
- 将 X=0, 现态 11 代入次态方程组和输出方程 , 得到次态 00,Z=1; 将 X=1, 现态 11 代入次态方程组和输出方程 , 得到次态 10,Z=0;
- 电路有自启动功能
5.4 中规模时序逻辑电路芯片-计数器¶
5.4.1 计数器介绍¶
- 什么是计数器 : 统计输入脉冲的个数
- 一种能在输入信号作用下依次通过预定状态的时序逻辑电路,是数字系统和计算机广泛使用的逻辑器件 可用于计数. 分频. 定时. 控制. 产生节拍脉冲(顺序脉冲)和序列脉冲等。
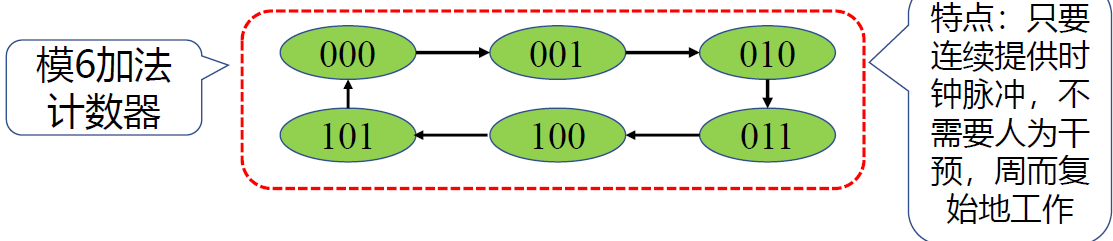
- 计数器特点
- 计数器在运行时,所经历的状态是周期性的,总是在有限个状态中循环。
- 将一次循环所包含的状态总数 称为计数器的"模" 记为M, 包含 n 个触发器的最大模值 𝑀=2𝑛。
- 把作用于计数器的时钟脉冲称为计数脉冲,用CP ( 或 CLK) 表示 。
- 计数器分类
- 按照计数器时钟控制方式分类:
- 同步计数器
- 异步计数器
- 按照计数器状态数分类:
- n 位二进制计数器
- 十进制计数器
- 任意进制计数器
- 异步二进制计数器: 由于触发器的状态翻转是由低位向高位逐级进行的,因此 , 计数速度较低。
- 若时钟脉冲的频率为 f , 则 𝑄0. 𝑄1. 𝑄2. 𝑄3输出脉冲的频率分别为 \(\frac12f . \frac14f . \frac18f . \frac1{16}f\),常称这种计数器为分频器。
- 按照计数器时钟控制方式分类:
5.4.2 同步计数器¶
- 同步二进制计数器设计思想
- 根据计数器的功能要求,n 位二进制计数器用 n 个存储单元电路组成,存储单元的状态表示二进制数,存储单元由触发器实现。
- 由于是同步计数器,输入时钟脉冲将同步加到各触发器的时钟输入端,因此只有通过控制触发器的驱动信号来达到控制触发器状态的目的。
- 驱动信号可以根据时序逻辑电路设计中提到的计数器方式通过 状态转移图 和 卡诺图 来获得。
- 工作原理:
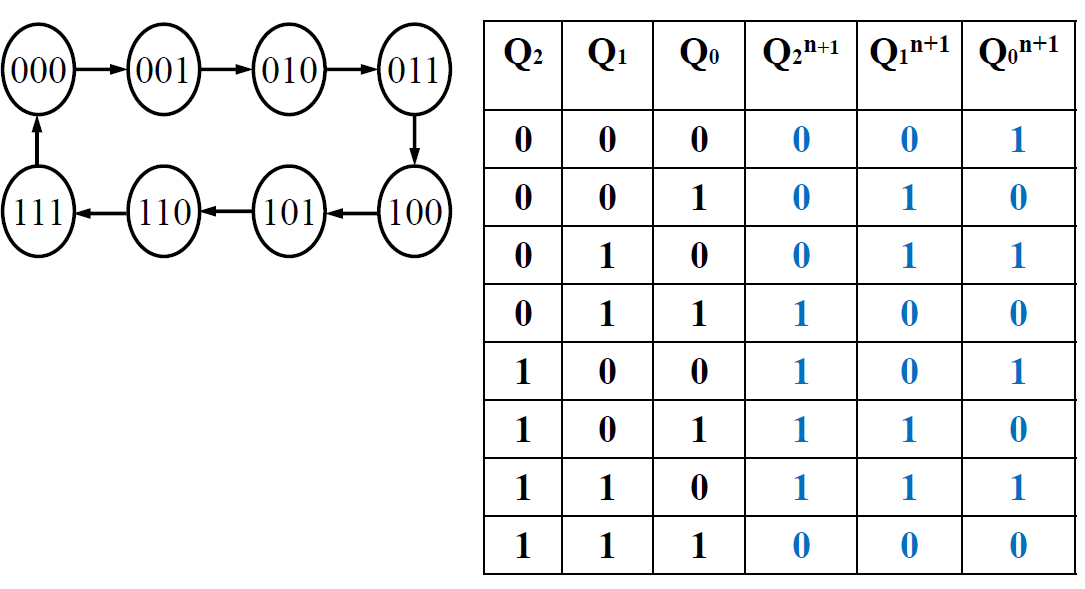 \(\begin{cases}Q_0^{n+1} = \overline{Q_0^n}\\
Q_1^{n+1} = Q_1^n\oplus Q_0^n\\
Q_2{n+1} = Q_2^{n}\oplus Q_1^n\cdot Q_0^n\\
\Rightarrow推广: Q_m^n+1 = Q_m^n\oplus Q_{n-1}^{n}...Q_1^nQ_0^n\end{cases}\)
\(\begin{cases}Q_0^{n+1} = \overline{Q_0^n}\\
Q_1^{n+1} = Q_1^n\oplus Q_0^n\\
Q_2{n+1} = Q_2^{n}\oplus Q_1^n\cdot Q_0^n\\
\Rightarrow推广: Q_m^n+1 = Q_m^n\oplus Q_{n-1}^{n}...Q_1^nQ_0^n\end{cases}\)- 由 n 个触发器构成的同步二进制计数器的模为 𝟐𝒏,没有多余状态,状态==利用率最高== , 同步计数器工作速度快
- 如果用 T 触发器构成的同步二进制加法计数器,驱动方程: - \(𝑇_0=1\) - \(𝑇_𝑖=𝑄_{𝑖−1}^𝑛𝑄_{𝑖−2}^𝑛⋯𝑄_0^𝑛(𝑖≠0)\)
- 用 JK 触发器 实现 n 位二进制同步加计数器,驱动方程为: \(𝐽_0=𝐾_0=1\\ 𝐽_1=𝐾_1=𝑄_0\\ 𝐽_2=𝐾_2=𝑄_1𝑄_0\\ 𝐽_3=𝐾_3=𝑄_2𝑄_1𝑄_0\\ ......\\ 𝐽_m=𝐾_m=𝑄_{𝑚−1}𝑄_{𝑚−2}⋯𝑄_1𝑄_0\)
- 用 D 触发器 实现 n 位二进制同步加计数器,驱动方程为: \(𝐷_0=𝑄_0\\ 𝐷_1=𝑄_1\oplus 𝑄_0\\ 𝐷_2=𝑄_2\oplus 𝑄_1𝑄_0\\ 𝐷_3=𝑄_3\oplus 𝑄_2𝑄_1𝑄_0\\ ......\\ 𝐷_𝑚=𝑄_{𝑚−1}\oplus 𝑄_{𝑚−2}𝑄_{𝑚−3}⋯𝑄_0\)
5.4.3 中规模同步计数器-74161(常用)¶
-
常用同步计数器芯片
芯片型号 计数进制 输出特点 置数方式 清零方式 74LS160 十进制 8421BCD 编码 同步 异步 74LS161 十六进制 4 位二进制码 同步 异步 74LS162 十进制 8421BCD 编码 同步 同步 74LS163 十六进制 4 位二进制码 同步 同步 - 清零方式:
- 异步清零: 只要 ① 清零端给出有效信号, 立刻清零
- 同步清零: ① 清零端给出有效信号 ② 时钟边沿到来, 才会清零
- 置数功能: ① 时钟边沿 与 ② 置数使能信号有效, 向计数器装入指定的初始值
- 清零方式:
-
常用芯片: 74161
- 电路符号和引脚符号 : 9 个输入端, 5 个输出端(⑭~⑪)
-
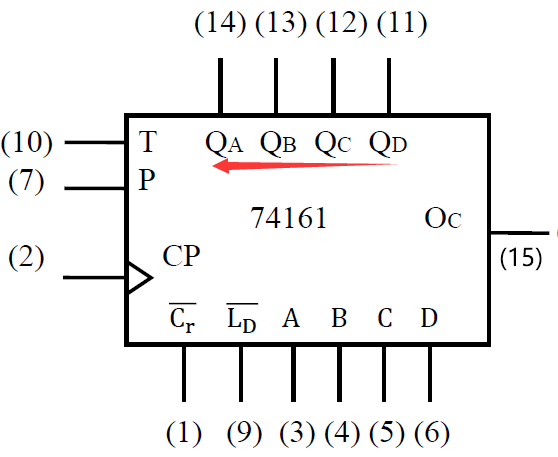 \(\begin{cases}⑭~⑪输出端: Q_DQ_CQ_BQ_A为数据输出端, 从高到低\\
⑮输出端O_C : 溢出进位输出端\\\\
②CP : 脉冲输入端\\
⑩T和⑦P: 使能输入端 \textcolor{orange}{(全为1时才会接收脉冲, 正常工作)}\\
①\overline{C_r} : 异步清零端 (低电平有效, 输入0清零)\\
⑨\overline{L_D} : 同步预置端 (低电平有效, 输入0置为预置的初始值)\end{cases}\)
\(\begin{cases}⑭~⑪输出端: Q_DQ_CQ_BQ_A为数据输出端, 从高到低\\
⑮输出端O_C : 溢出进位输出端\\\\
②CP : 脉冲输入端\\
⑩T和⑦P: 使能输入端 \textcolor{orange}{(全为1时才会接收脉冲, 正常工作)}\\
①\overline{C_r} : 异步清零端 (低电平有效, 输入0清零)\\
⑨\overline{L_D} : 同步预置端 (低电平有效, 输入0置为预置的初始值)\end{cases}\) - 逻辑功能
-
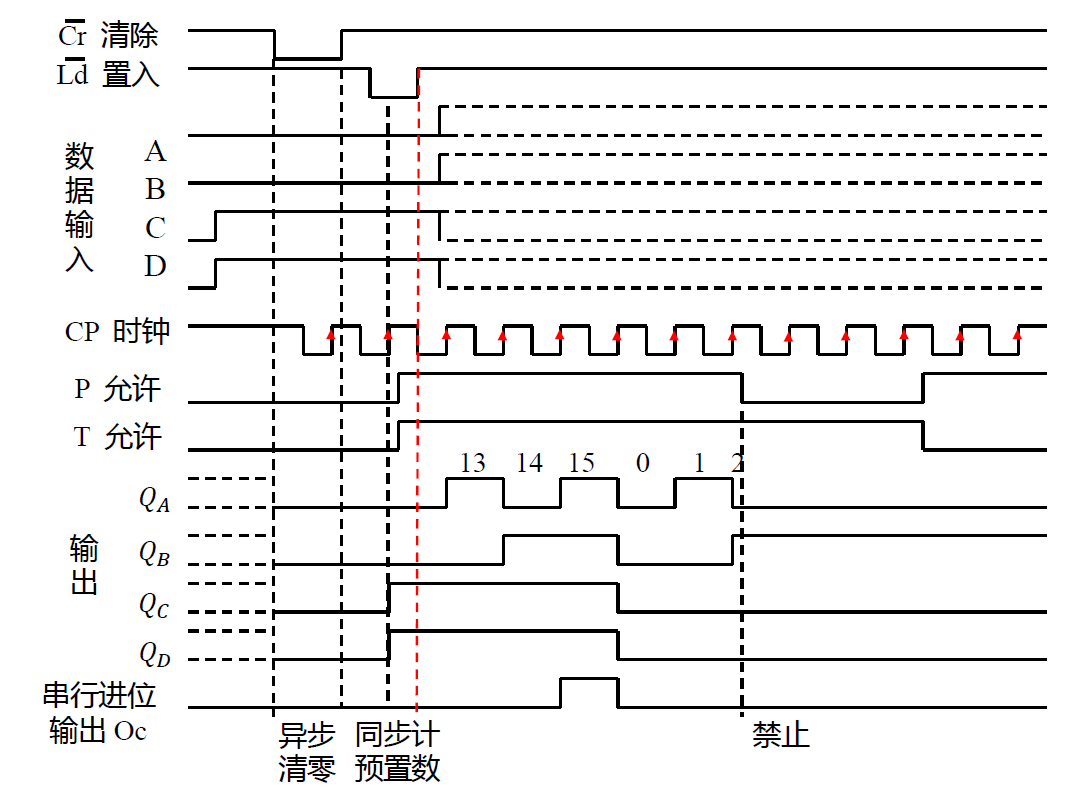
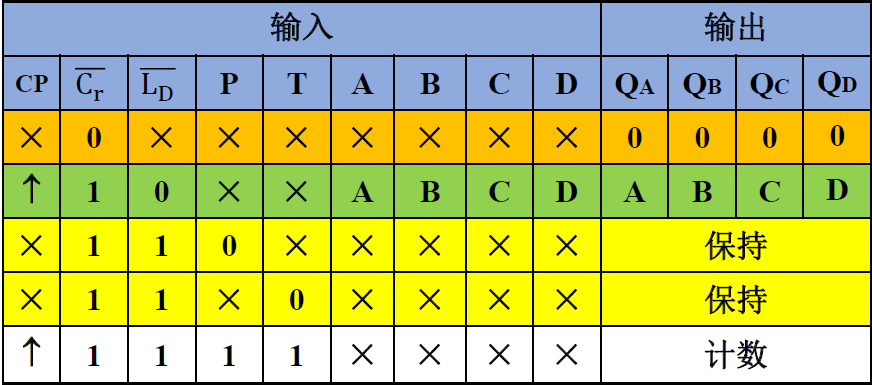 -
- 
- 电路符号和引脚符号 : 9 个输入端, 5 个输出端(⑭~⑪)
-
-
应用
-
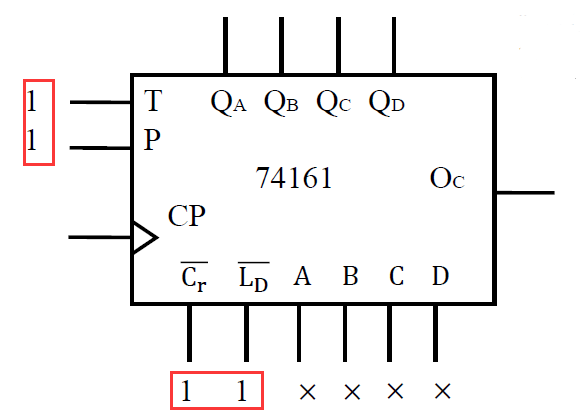
基础: 构成十六进制计数器
- 输出按 𝑄𝐷𝑄𝐶𝑄𝐵𝑄𝐴的高低顺序计数,输出依次为 0000~1111 -
-
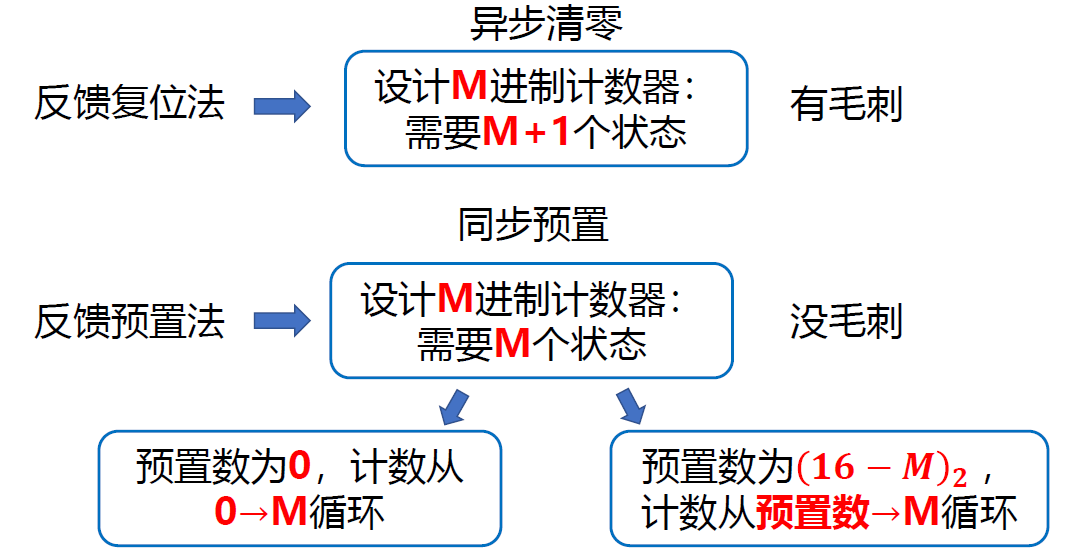
构成十进制计数器
1. 采用反馈复位法 (使用清零\(\overline{C_r}\))
- <img src="数字电路与逻辑设计.assets\image-20221107160828863.png" alt="image-20221107160828863" style="zoom:50%;" /> - 异步清零, 当计数器跳到 1010(10)时, 进位, 清零 <img src="数字电路与逻辑设计.assets\image-20221107160915631.png" alt="image-20221107160915631" style="zoom:50%;" /> - 使用反馈复位法设计 M 进制计数器 ==需要 M+1 个状态== <font color='orange'>(需要一个状态用来判断清零)</font> - 此外, 由于清零为异步清零, 监测的是第 M+1 个, 会有一瞬间到达第 M+1 个状态, 波形==存在毛刺==2. 采用反馈预置法 (使用预置\(\overline{L_D}\))
- <img src="数字电路与逻辑设计.assets\image-20221107161756428.png" alt="image-20221107161756428" style="zoom:50%;" /> - ①: 遇到 1001 时, $\overline{L_D} = 0$, 下一个波沿到来时, 原本应该变为 1010, 但是预置, 变为 0000 ②: 遇到 16 时, 进位 O~C~ = 1, 下一个状态原本应该是(1)0000, 但是预置, 变为 0110 (0110->1111, 6->15, 10 个状态) - 由于预置为同步预置, 监测的是第 M 个状态, 不会出现毛刺3. > 构成 256 进制计数器(28 = 162 = 256)
- 采用同步连接法: <img src="数字电路与逻辑设计.assets\image-20221107164606374.png" alt="image-20221107164606374" style="zoom:50%;" /> - 当低位的芯片有进位时, 高位芯片才能计数 1 次 - 采用异步连接法: <img src="数字电路与逻辑设计.assets\image-20221107164709108.png" alt="image-20221107164709108" style="zoom:50%;" /> - 将低位的进位作为脉冲, 进行计数
-
-
总结:
5.4.4 异步计数器¶
-
异步二进制计数器
- 异步二进制计数器可由 𝑇′触发器(JK 亦可)构成 , 触发器之间串接 , 低位触发器的输出 , 作为高位触发器的时钟。
-
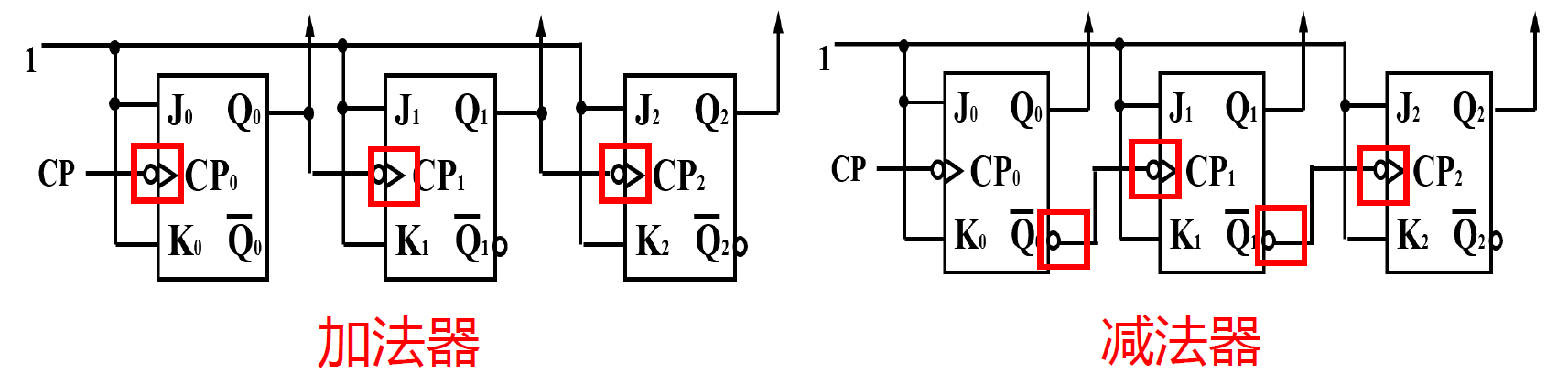
加法计数器:\(奇数个圈\Rightarrow 加法器\)
- 当采用 下降沿 触发器时,将 𝑸𝒊−𝟏和 𝑪𝑷𝒊 (1 个圈)相连;
- 当采用 上升沿 触发器时,将 𝑸𝒊−𝟏和 𝑪𝑷𝒊 (0 个圈)相连。
-
减法计数器:\(偶数个圈\Rightarrow 减法器\)
- 当采用 下降沿 触发器时,将 𝑸𝒊−𝟏和 𝑪𝑷𝒊(一个圈)相连;
- 当采用 上升沿 触发器时, 将 𝑸𝒊−𝟏和 𝑪𝑷𝒊 (0 个圈)相连。
- 圈: 两个触发器之间相连部分 图中的的反相标记(\(\circ\))
-
异步十进制出发器(多个二进制构成)
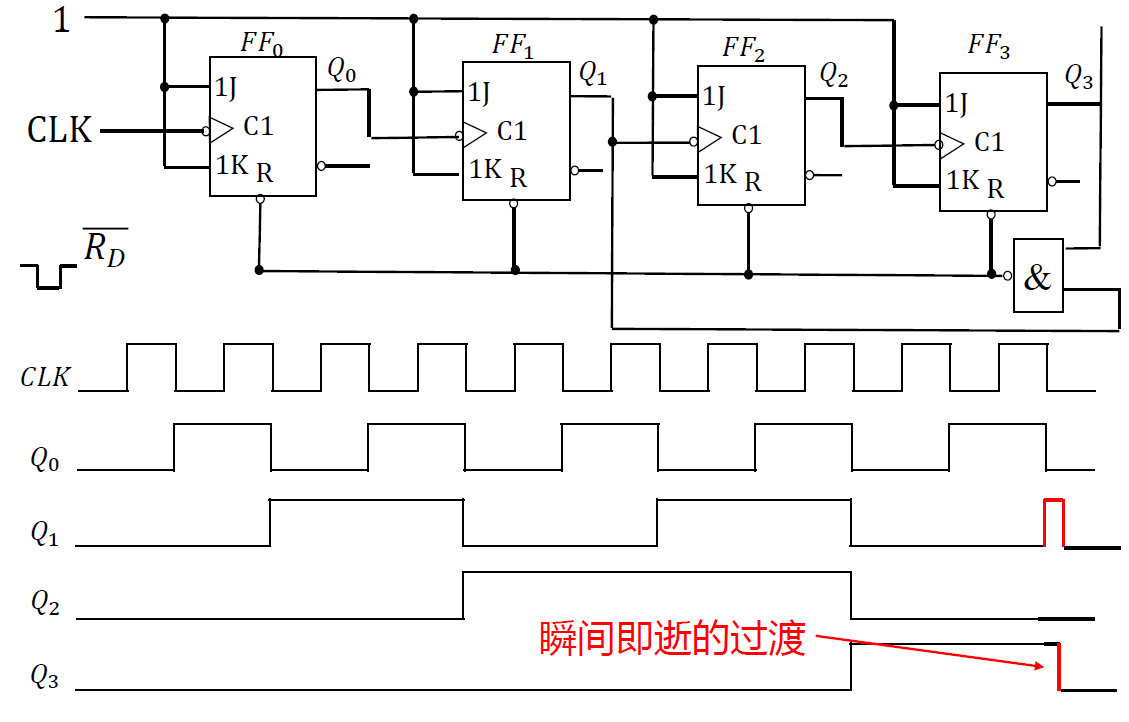
- 异步 存在毛刺
5.4.5 中规模异步计数器-7490¶
-
二-五-十进制异步计数器(
7490芯片)-
电路符号和引脚符号: 6 个输入端, 4 个输出端 (本质是由一个二进制 + 一个五进制构成)
-
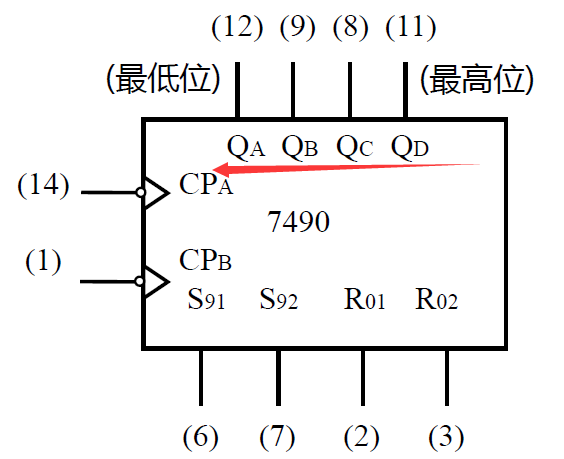 $ \begin{cases} QA \& Q_B Q_C Q_D 为数据输出端\\
S 和 S{92} 为直接置位端 (只能置 9)\
R 和 R{02} 为直接复位端\\
CP 和 CP{B} 分别为独立脉冲输入端,下降沿有效\
\qquad CP 输入, QA 二进制输出\
\qquad CP$} 输入, Q_BQ_CQ_D 实现五进制输出 \end{cases
$ \begin{cases} QA \& Q_B Q_C Q_D 为数据输出端\\
S 和 S{92} 为直接置位端 (只能置 9)\
R 和 R{02} 为直接复位端\\
CP 和 CP{B} 分别为独立脉冲输入端,下降沿有效\
\qquad CP 输入, QA 二进制输出\
\qquad CP$} 输入, Q_BQ_CQ_D 实现五进制输出 \end{cases -
逻辑功能 -
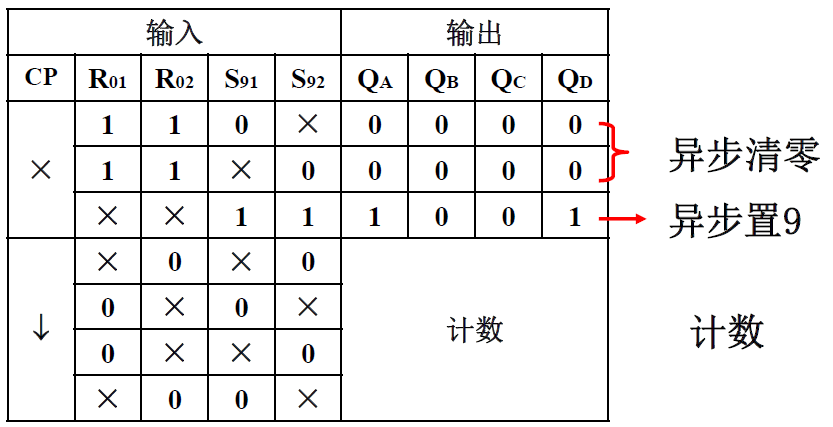 - 只能置 9, 不能预置值(所以不能使用反馈预置法)
- 只能置 9, 不能预置值(所以不能使用反馈预置法) - 基本应用
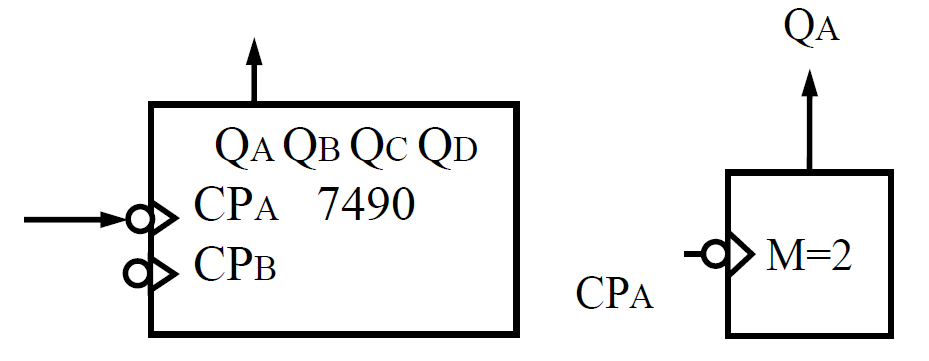
- 1 位二进制计数器
-
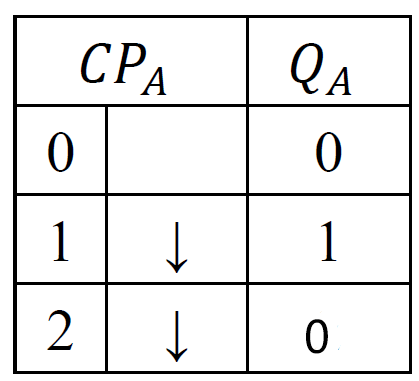 - 1 位五进制计数器
-
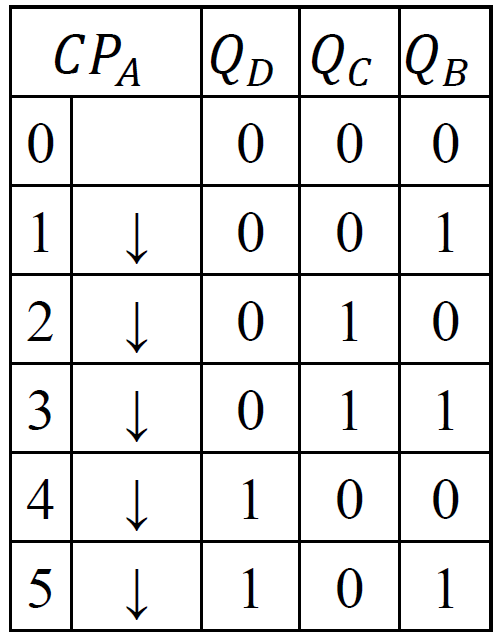
- 1 位五进制计数器
- 
-
-
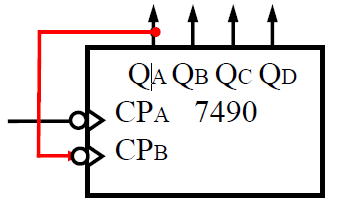
构成一位 8421 码 十进制计数器
- 将 𝑄𝐴与 𝐶𝑃𝐵相连,计数脉冲从 𝐶𝑃𝐴输入。 𝑄𝐷𝑄𝐶𝑄𝐵𝑄𝐴输出,构成 8421 码计数器。(也就是异步实现)
- 𝑄𝐷𝑄𝐶𝑄𝐵𝑄𝐴

-
构成一位 5421 码十进制计数器
- 将 𝑄𝐷与 𝐶𝑃𝐴相连,计数脉冲从 𝐶𝑃𝐵输入。 𝑄𝐷𝑄𝐶𝑄𝐵𝑄𝐴输出,构成 5421 码计数器
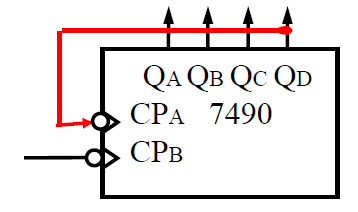
- 𝑄𝐴𝑄𝐷𝑄𝐶𝑄𝐵
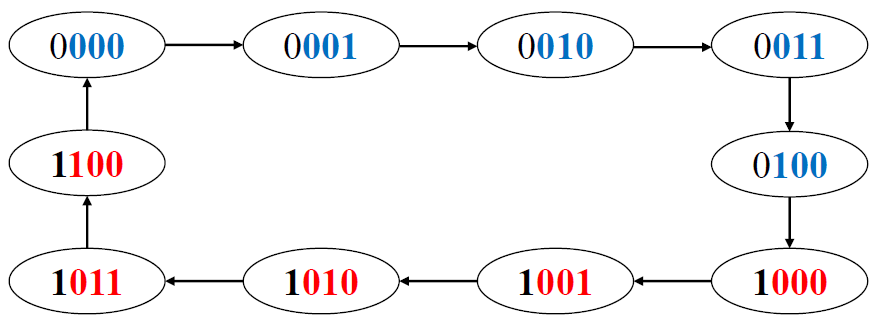
- A 作为高位
-
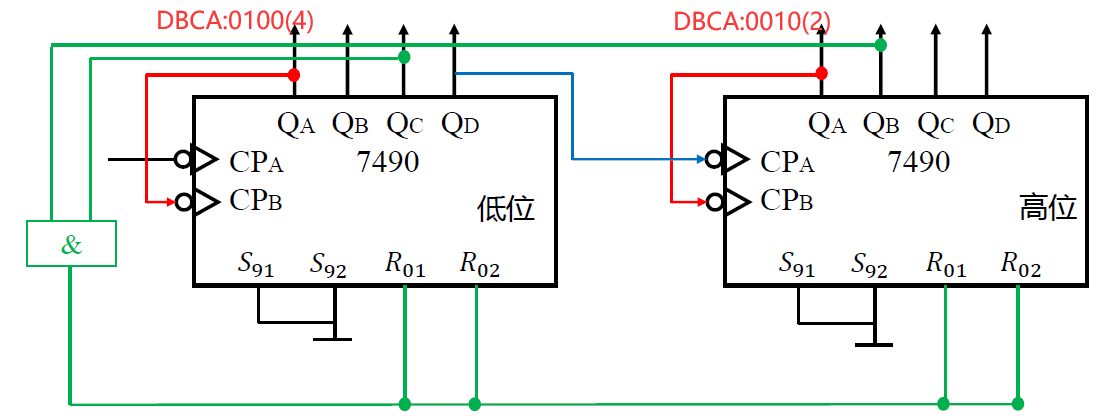
总结: 用 74LS90 实现任意模(M)的计数器
- 只能使用==反馈归零法(复位法)==
- 1~10 以内的 M 进制
- 把 M 进制所对应的输出端为 1 的输出相与后反馈到清零端,作为计数满整清零信号。
- 10 到 100 以内的 M 进制
- 由两片(个位和十位)
74LS90扩展成 100 进制; 扩展连接方法:两芯片均连接成十进制,时钟脉冲从个位 𝐶𝑃0进,个位的 𝑄3 与十位芯片的 𝐶𝑃0 相连即可。 - 把 M 进制所对应的十位,个位芯片上输出为 1 的端相与后==反馈到清零端== ,作为个位和十位的计数满整清零信号。
- 由两片(个位和十位)
- 注意 :由于 7490 是异步清零,对于 M 进制, M 数值用于清零,计数为 0 到 M-1
-
构成九进制计数器
- 九进制的输出端为 1001 ,将 𝑄𝐷. 𝑄𝐴输出相与后反馈到清零端,作为计数满整清零信号。
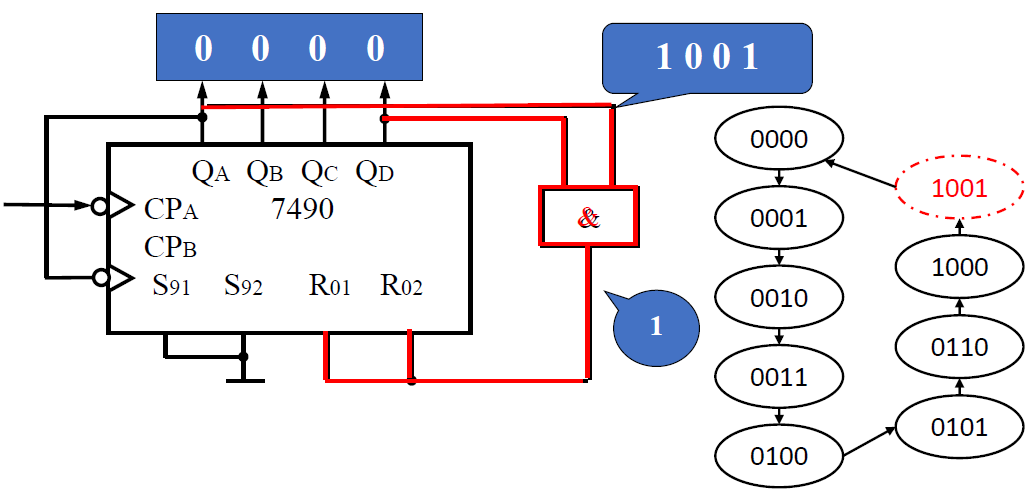
-
构成二十四进制计数器
-
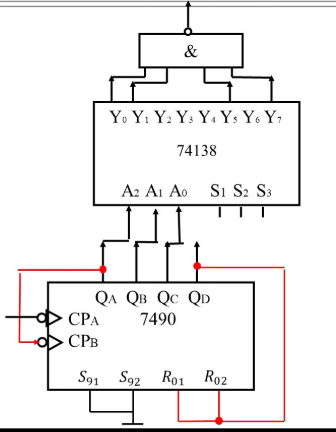
计数型序列发生器 : 和 3-8 译码器构成的序列信号产生器
11000101-
序列长度为八位, 模八计数, 使用 3-8 译码器筛选需要的状态来输出
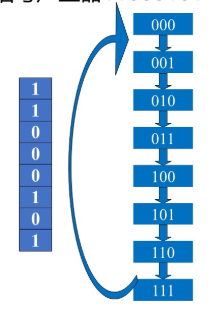 需要 000, 001, 101, 111 四个状态映射为 1, 其余状态为 0
需要 000, 001, 101, 111 四个状态映射为 1, 其余状态为 0
-
5.5 中规模时序逻辑电路芯片-寄存器¶
5.5.1 寄存器¶
- 寄存器是计算机的一个重要部件,用于暂时存放一组二值代码(如参加运算的数据. 运算结果. 指令等)
- 由 触发器 和 控制门 组成寄存器 \(\begin{cases}基本寄存器\\移位寄存器 \begin{cases}单向移位寄存器\\双向移位寄存器\end{cases} \end{cases}\)
- 基本寄存器的操作:读出 / 写入 / 复位(清零)
- 移位寄存器的操作:读出 / 写入 / 复位(清零) / 左移(右移)
5.5.2 基本寄存器¶
- 基本寄存器: 一个 𝒏 位寄存器由𝒏 个触发器构成,能存放 𝒏 位二进制数。
- 各种触发器均能够构成寄存器, 用 D 触发器最简单
5.5.3 移位寄存器基本介绍¶
一. 移位寄存器¶
- 移位寄存器: 除了寄存器的功能外,存放的二进制数码可以进行==移位== 。
- 按照移位的方向分类: \(\begin{cases}单向移位寄存器\\双向移位寄存器\end{cases}\)
-
按工作方式分类:
\(输入方式:\begin{cases}串行输入\\并行输入\end{cases} + 输出方式:\begin{cases}串行输出\\并行输出\end{cases}\Rightarrow 工作方式: \begin{cases}①串入-串出\\②串入-并出\\③并入-串出\\④并入-并出\end{cases}\)
二. 单向移位寄存器¶
-
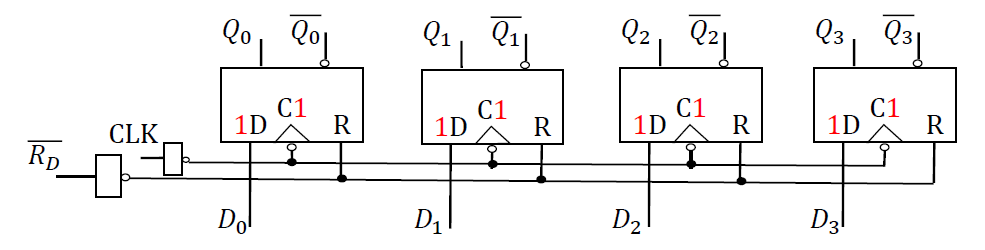
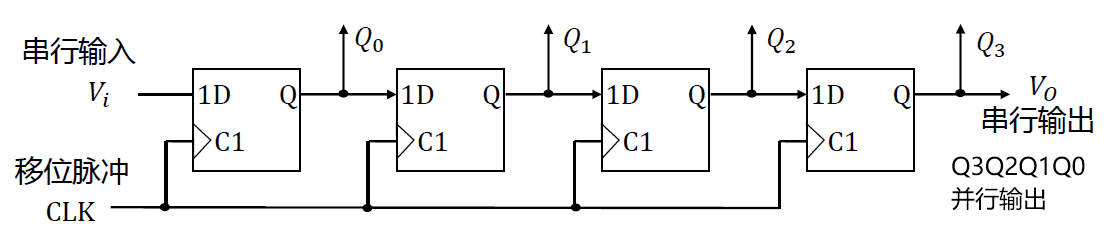
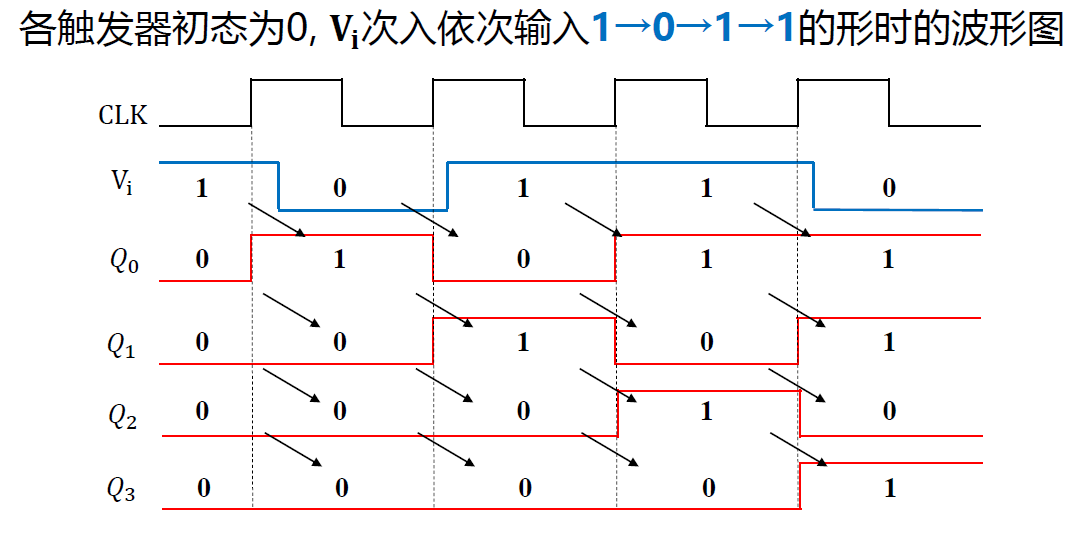
串入—串/并出 单向寄存器(右移寄存器)
-
各触发器的状态方程为:
\(Q_0^n+1=𝐷_0=𝑉_i(输入)\\Q_1^n+1=𝐷_1=Q_0^n\\Q_2^n+1=𝐷_2=Q_1^n\\Q_3^n+1=𝐷_3=Q_2^n\)
- 右移状态方程 : \(𝑄_𝑖^{𝑛+1}=𝑄_{𝑖−1}^𝑛\) (低位向高位进, \(Q_0Q_1Q_2Q_3 →, 低到高排列时的向右转移\))
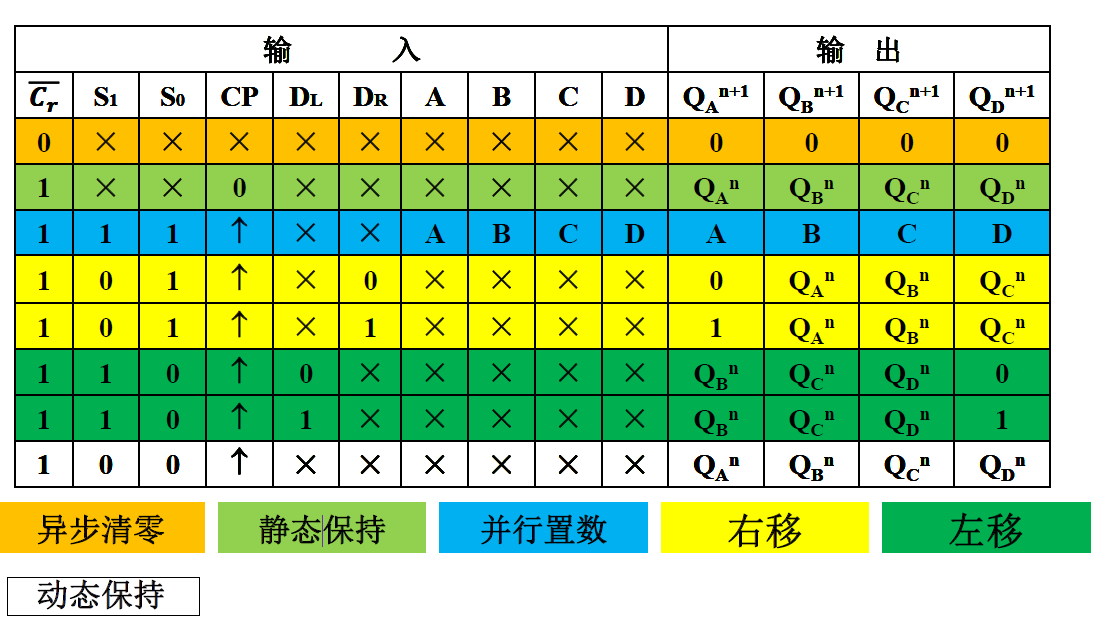
三. 双向移位寄存器-74194¶
- 内部结构原理: n 组 D 触发器+数据选择器
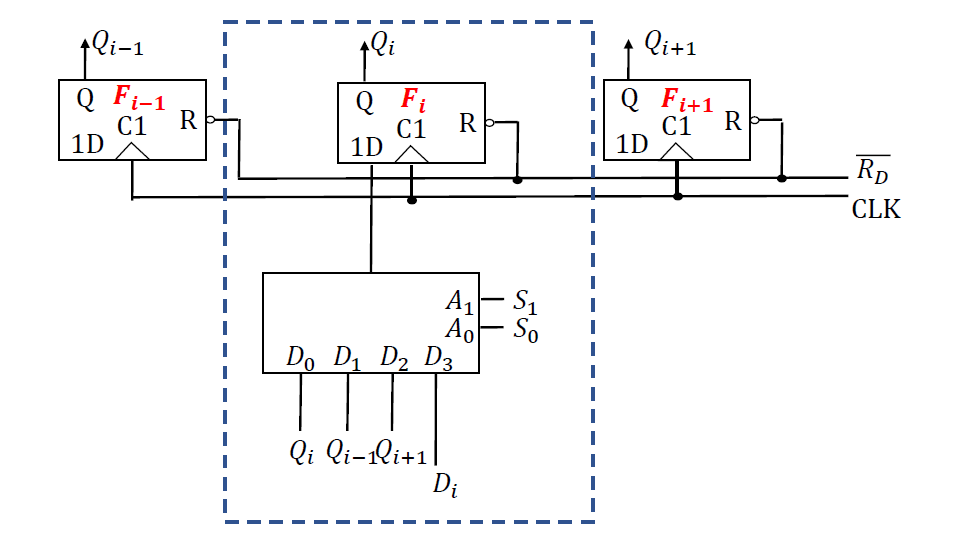
- S1S0为 00 ,01,10,11 实现寄存器的 保持,右移,左移 和 并行置数 模式
- 电路符号及引脚含义: 16 个引脚的集成芯片 10 个输入端, 4 个输出端
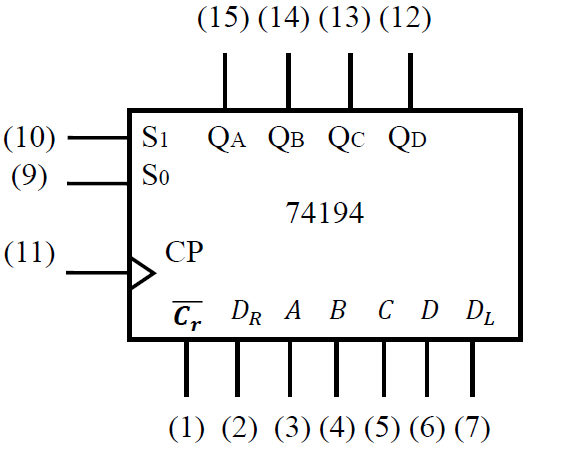 \(\begin{cases} 𝑄_𝐴𝑄_𝐵𝑄_𝐶𝑄_𝐷为并行数据输出端\\
𝑄_𝐴为左移串行数据输出端\\
𝑄_𝐷为右移串行数据输出端 \\\\
𝐴~𝐷为并行数据输入端\\
𝐷_𝑅为右移串行数据输入端\\
𝐷_𝐿为左移串行数据输入端\\\\
\overline{C_r}异步清零端\\
𝑆_1𝑆_0为使能输入端(控制端)\\
\qquad 𝑆_1𝑆_0=01\ 右移\quad 𝑆_1𝑆_0=10\ 左移\\
\qquad𝑆_1𝑆_0=11\ 并行置数\end{cases}\)
\(\begin{cases} 𝑄_𝐴𝑄_𝐵𝑄_𝐶𝑄_𝐷为并行数据输出端\\
𝑄_𝐴为左移串行数据输出端\\
𝑄_𝐷为右移串行数据输出端 \\\\
𝐴~𝐷为并行数据输入端\\
𝐷_𝑅为右移串行数据输入端\\
𝐷_𝐿为左移串行数据输入端\\\\
\overline{C_r}异步清零端\\
𝑆_1𝑆_0为使能输入端(控制端)\\
\qquad 𝑆_1𝑆_0=01\ 右移\quad 𝑆_1𝑆_0=10\ 左移\\
\qquad𝑆_1𝑆_0=11\ 并行置数\end{cases}\)- 注意使能控制端的位置(不一定是 S1在上)
- 逻辑功能
四. 移位寄存器的应用¶
1. 移位寄存器计数器¶
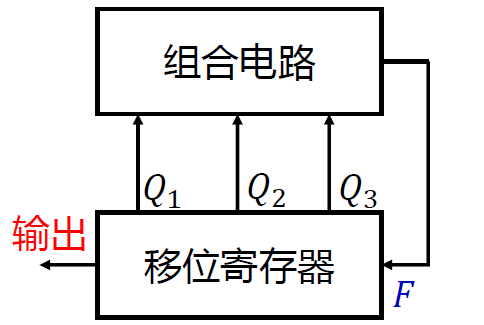
- 移位寄存器型计数器: 是指在移位寄存器的基础上加反馈电路而构成的具有特殊编码的同步计数器。
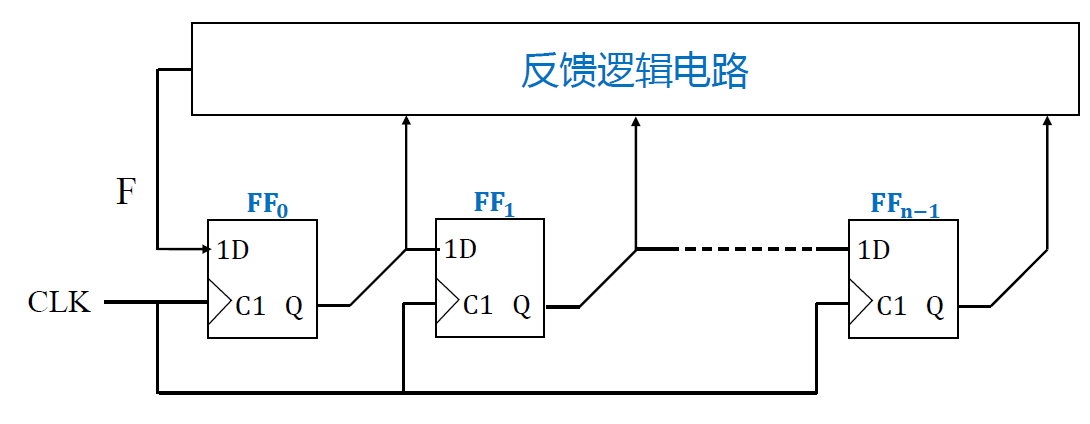
- F : 反馈函数, 输入到移位的开头
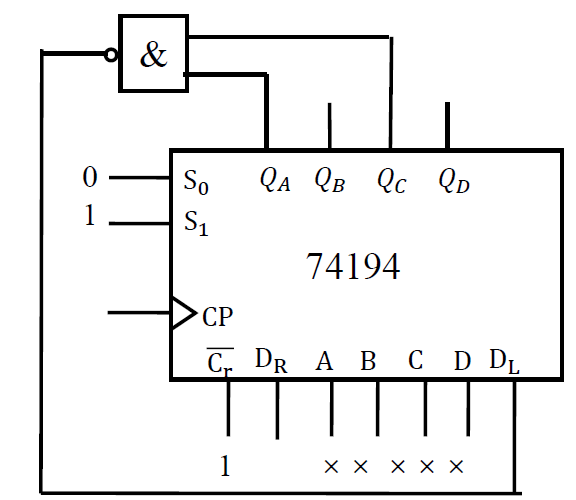
环形计数器¶
-
电路组成(以四位环形计数器为例)
-
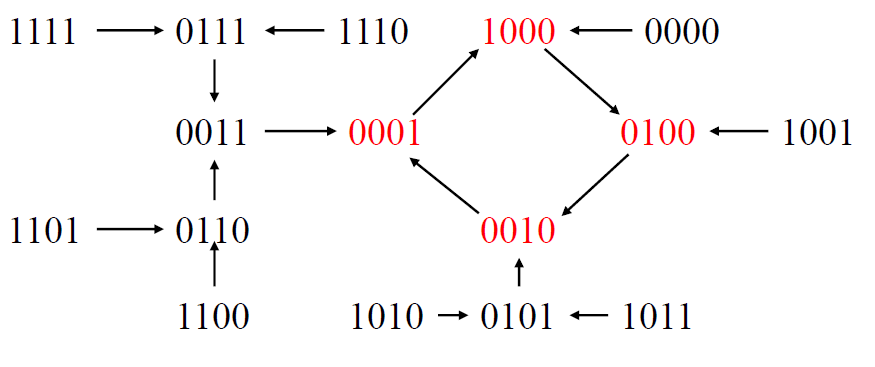
状态图(\(Q_0Q_1Q_2Q_3\)): 分为有效循环和无效循环
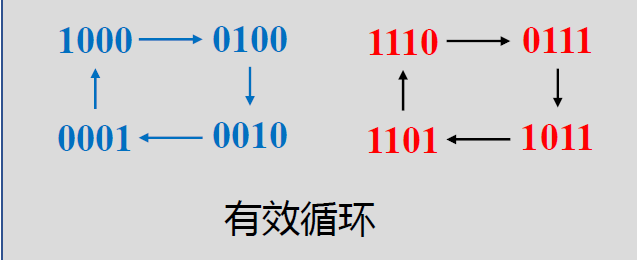

- 有效循环: 按照译码器方式(只有一个为 1/0. 其余都为 0/1) 编码状态的循环
- 无效循环: 其他循环
-
实现环形计数器的自启动 (提高部分) 重新设计反馈电路
-
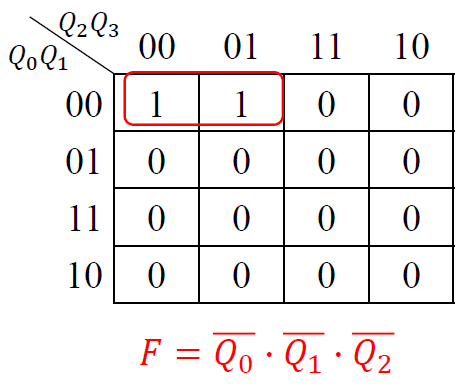
列表确定反馈函数 F :

-
求 F 的最简表达式 : \(F = \overline{Q_0}\cdot \overline{Q_1}\cdot \overline{Q_2}\)
-
-
画状态转换图 (验证自启动)
- \(Q_0Q_1Q_2Q_3\qquad Q_0^{n+1} = F = \overline{Q_0}\cdot \overline{Q_1}\cdot \overline{Q_2}\)
*
-
画逻辑电路图
-
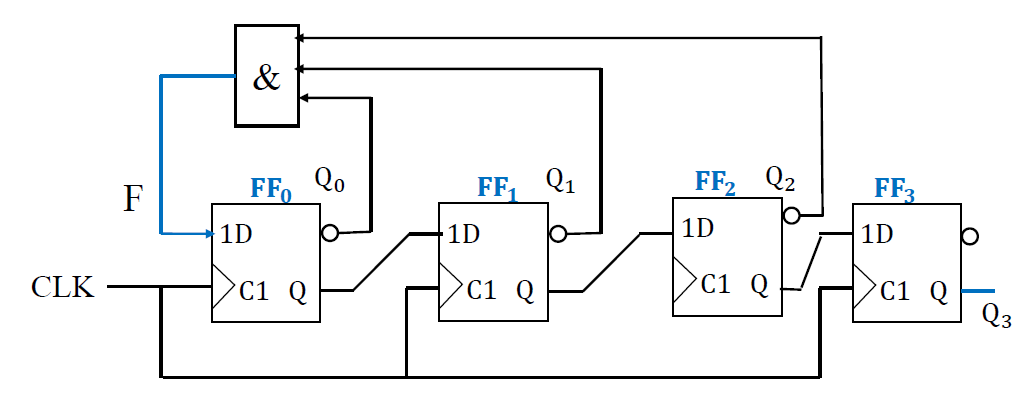
-
-
思考题: 怎么使用 74194 实现上述功能
- \(Q_A^{n+1} = F = \overline{Q_0}\cdot \overline{Q_1}\cdot \overline{Q_2}\)
- 右移: \(S_1S_0 = 01\)
- \(D_R = \overline{Q_0}\cdot \overline{Q_1}\cdot \overline{Q_2} = \overline{Q_A+Q_B+Q_C}\)
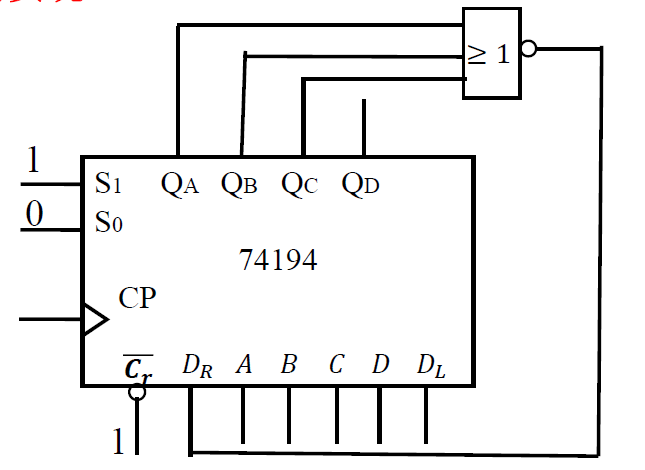
-
总结:
- 环形计数器附带有译码器功能
- 环形计数器的输出波形为顺序脉冲;
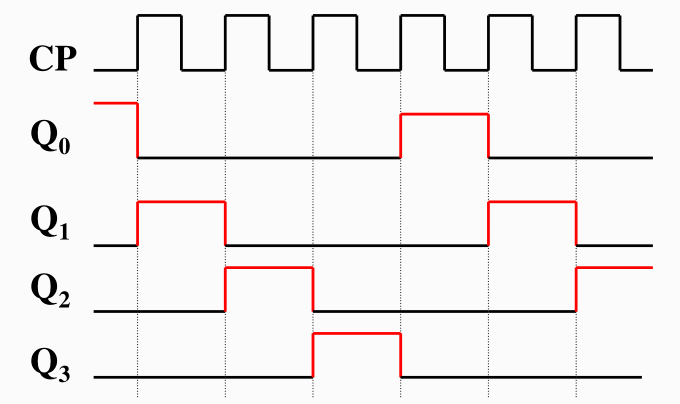
- 常称环形计数器为 顺序脉冲发生器
- 环形计数器的缺点是状态利用效率低,n 个触发器构成的环形计数器仅有 n 个有效状态,有==𝟐𝐧−𝐧 个无效状态== 。
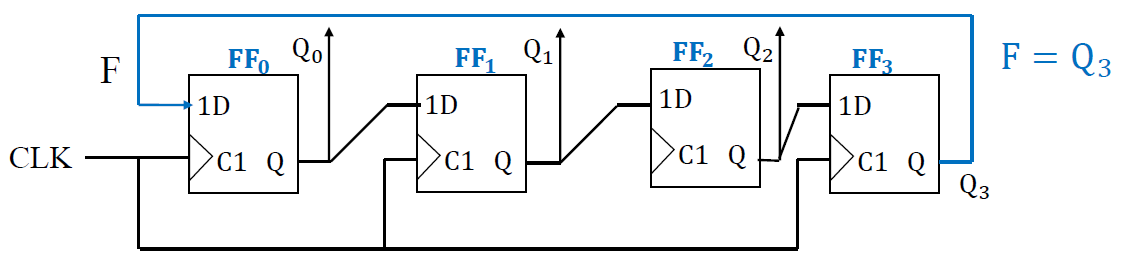
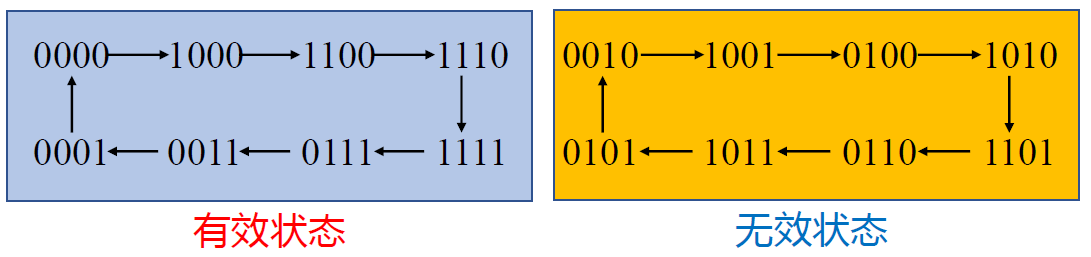
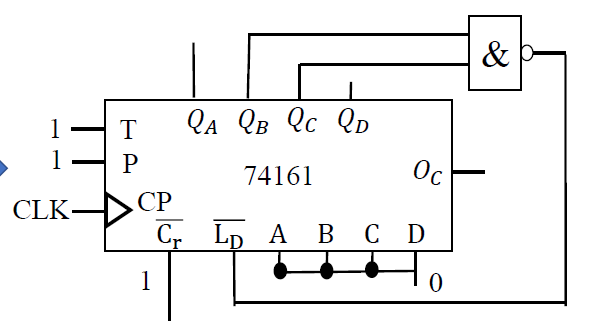
扭环形计数器¶
- 电路组成(以四位扭环形计数器为例)
- \(F = \overline{Q_3}\)
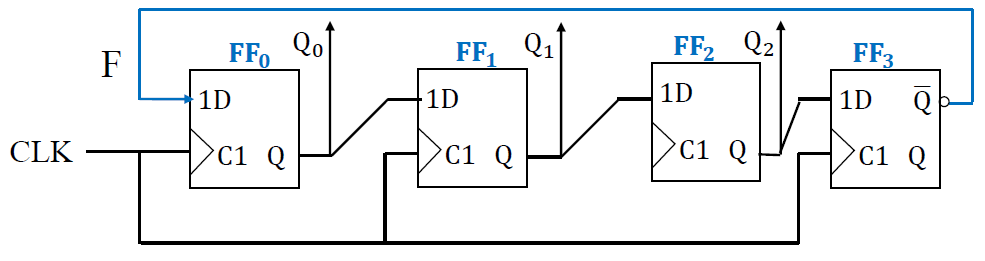
-
状态图 (\(Q_0Q_1Q_2Q_3\))
- 状态变化跟格雷码相似, 两个状态之间只有一位会变化
-
使用 74191 构成扭环形计数器
- \(D_R = F = \overline{Q_3}\)
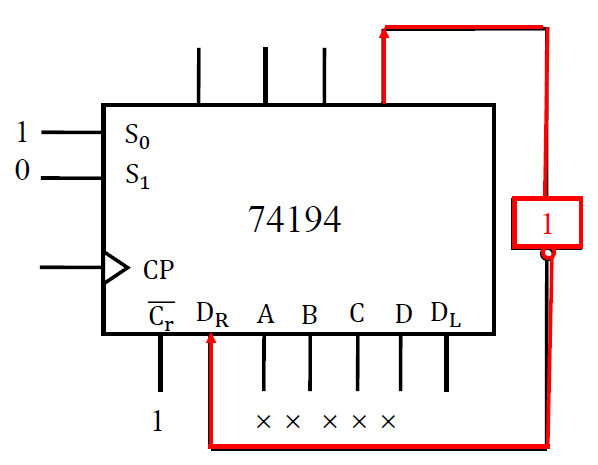
- 该电路无法自启动,需要重新设计反馈逻辑
- 总结
- 扭环形计数器输出码为循环码,能有效防止冒险现象;
- 扭环形计数器的输出波形为:
-
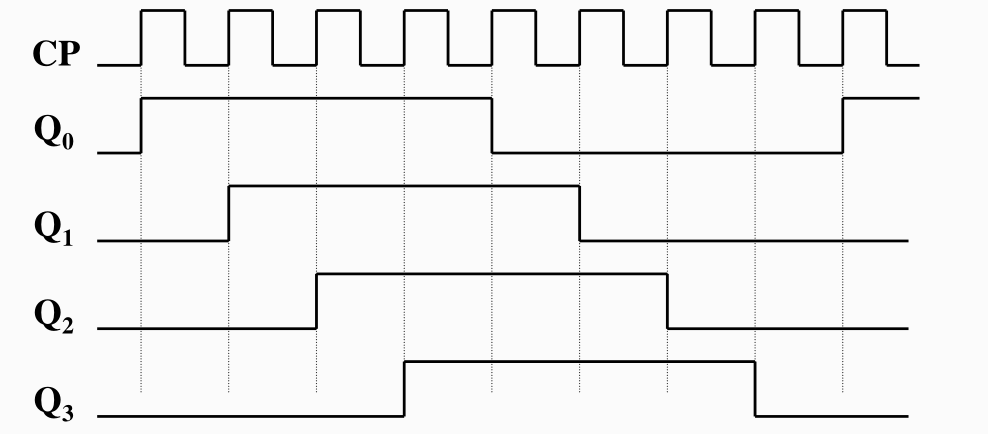
- 扭环形计数器状态的利用效率比环形计数器高, n 个触发器构成的扭环形计数器有 2n 个有效状态 , 有==𝟐𝐧−𝟐𝐧 个无效状态== 。
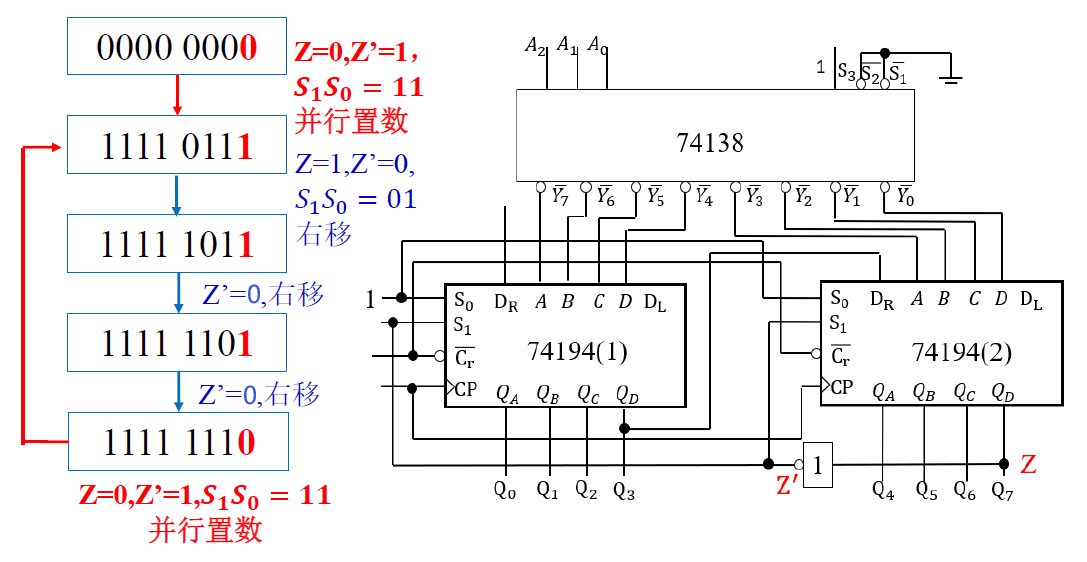
奇数分频器¶
-
七分频器波形图
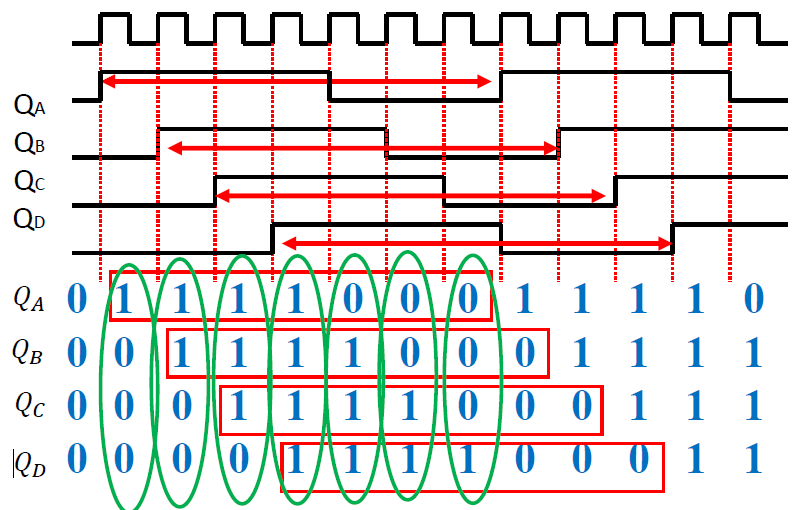 \(Q_A \rightarrow Q_B \rightarrow Q_C \rightarrow Q_D , D_R \rightarrow Q_A\)
\(Q_A \rightarrow Q_B \rightarrow Q_C \rightarrow Q_D , D_R \rightarrow Q_A\)
-
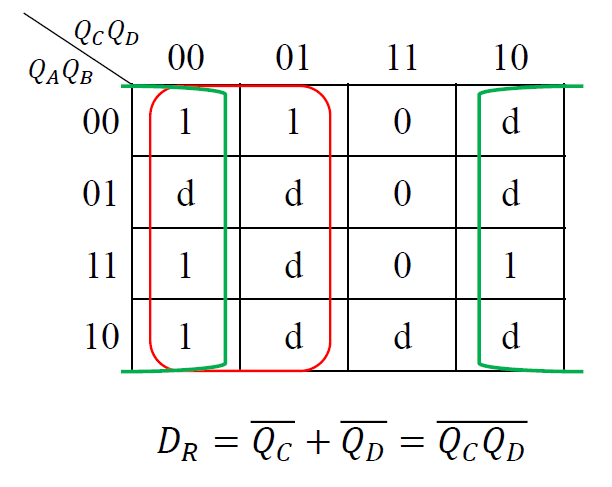
七分频状态表
- 对移位时存入的值进行讨论和计算
-
卡诺图化简:
- \(𝐷_𝑅=\overline{𝑄_𝐶}+\overline{𝑄_𝐷}=\overline{𝑄_𝐶𝑄_𝐷}\)
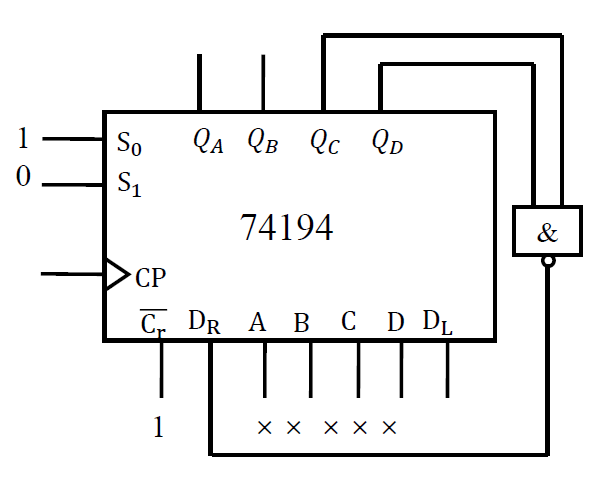
-
逻辑电路图(74191 实现)
可编程分频器¶
-
通过输入的二进制编码,控制 74194 按要求进行相应的移位循环,输出对应编码的分频频率。
- 通过工作状态的变化实现控制:移位状态 → 并行置入 → 移位状态 → 并行置入
- 通过对 74194 的控制端 𝑆1𝑆0=01,10,11 赋予不同的值,从而实现控制进入不同的工作状态
- 三分频为例,
011103 次循环后有一个 1 置入。需要循环 3 位后出现一个 0, 可以借用 74138 的译码器功能把 0 输出定位在第 3 位。- 11110111(并行置入) → 11111110(循环移位) → 11110111(并行置入)
-
设计实现三分频
并行输入 → 串行输出¶
序列码发生器¶
例: 设计一个产生 0101101 序列码的序列码发生器
-
序列长度为 7 ,选用 74161 计数器设计成模 7 计数器
-
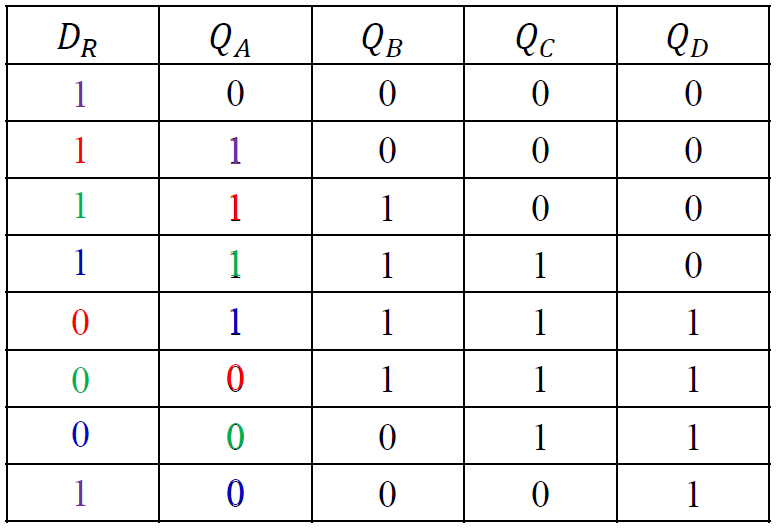
法一: 设计组合输出电路
-
电路状态以及输出真值表
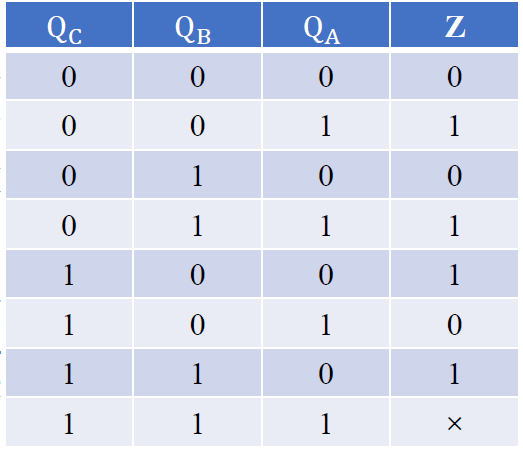
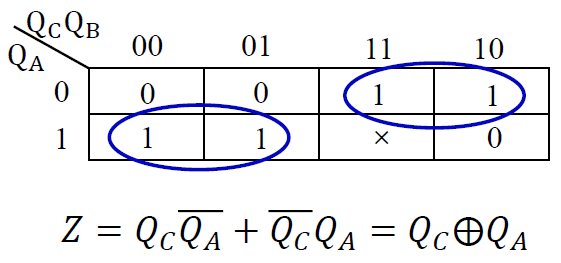
- 在模 7 计数器基础上加入逻辑输出电路
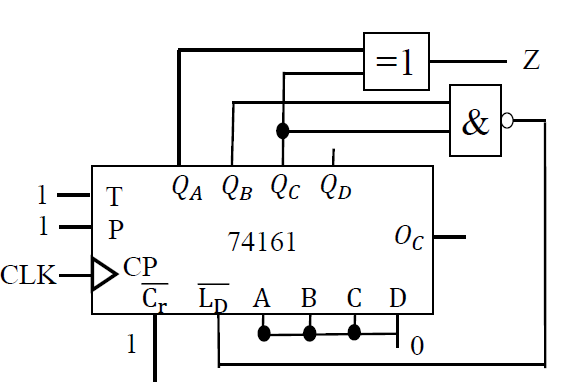 \(Z = Q_A\oplus Q_C\)
\(Z = Q_A\oplus Q_C\)
-
-
法二: 数据选择器实现
- 使用 74251 八选一数据选择器
- Z = Y = 0 1 0 1 1 0 1
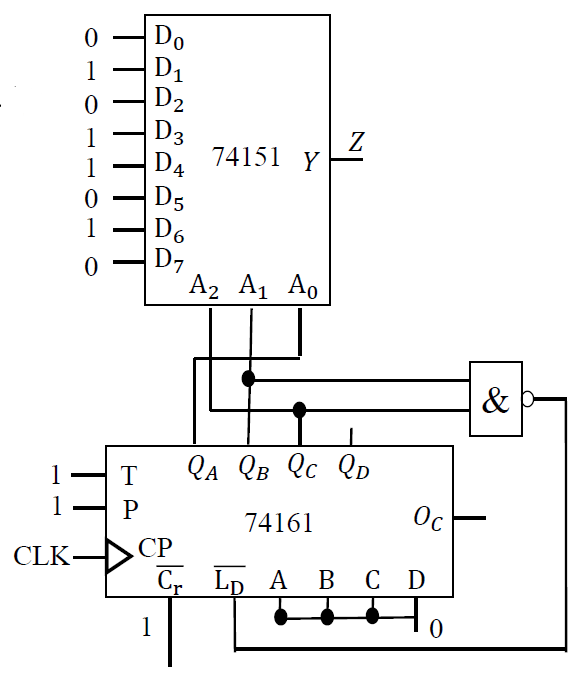
-
法三: 使用变量译码器实现
- 使用 74138 变量译码器
- \(Z = Y_1 + Y_3 + Y_4+Y_6 = \overline{\overline{Y_1}\cdot\overline{Y_3}\cdot\overline{Y_4}\cdot\overline{Y6}}\)
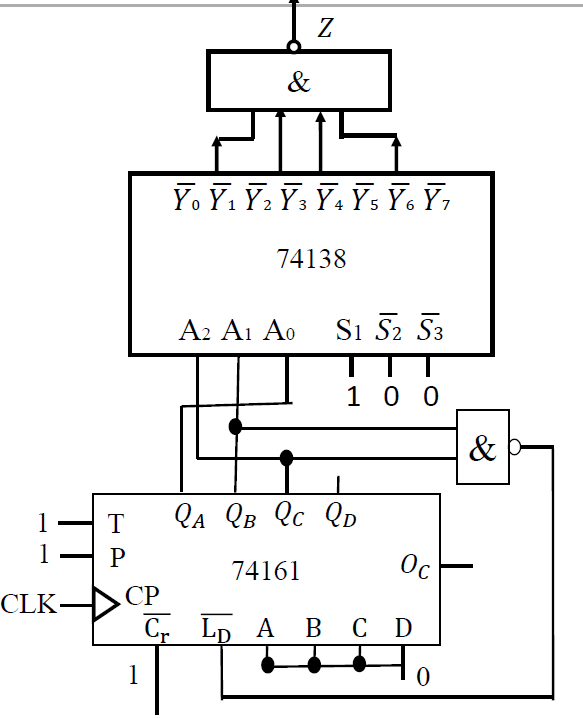
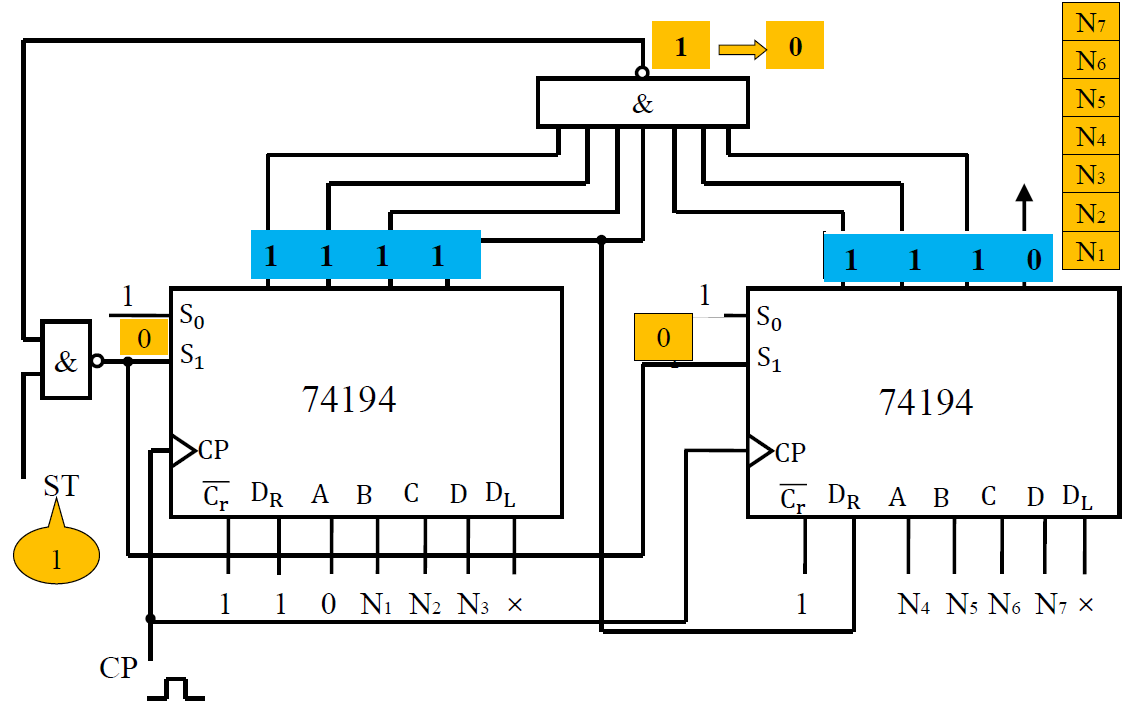
2. 移位寄存器型序列发生器¶
例:试设计一个能产生序列信号为 10110 的移位寄存器型序列信号发生器。
-
设计方法:序列长度为 L=5 ,考虑移位寄存器的级数(触发器个数)为 n ,应满足关系式 2𝑛≥𝐿,考虑用 3 位移位寄存器
- 以左移为例,𝐹→𝑄3→𝑄2→𝑄1→ 输出 。则要进一步分析 𝐹 函数
-
状态划分 :
-
由于序列长度为 5,先对序列按 3 位划分
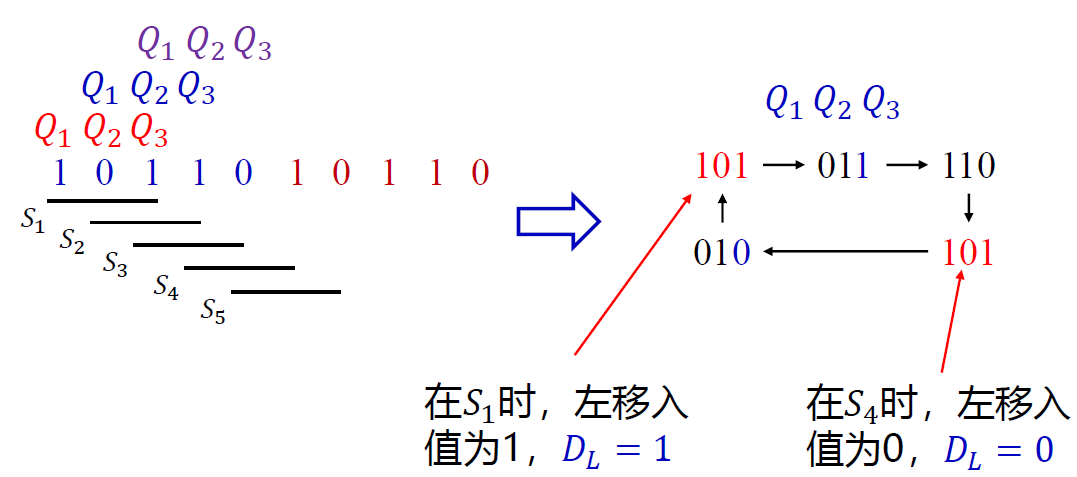
-
只使用 3 位会发生冲突 加 1 位避免
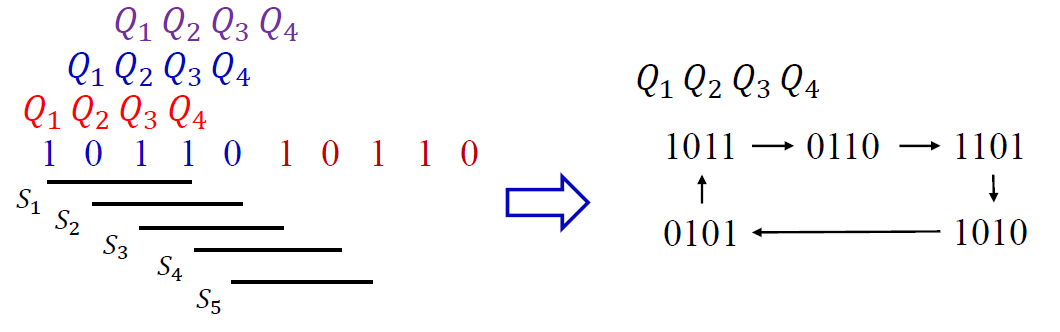
-
-
求出反馈逻辑 F
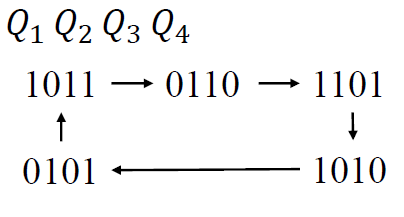 →
→ 
-
如用
74194,则首先设置左移 𝑆1𝑆0=10 𝑄𝐴为输出,对应的\(𝐷_𝐿=\overline{𝑄_𝐴𝑄_𝐶}\)
常用芯片¶
-
基本门电路
逻辑 芯片名 与 7408 或 7432 非 7404 与非 二输入: 7400
四输入: 7420异或 7486 -
组合逻辑
功能 芯片 全加器 74283 24 译码器(双) 74139 38 译码器 74138 
4 选 1 数据选择器 74153 
8 选 1 数据选择器 74151 
74251: 使能端高电平时, 输出高阻态 -
时序逻辑
功能 芯片 边沿 D 触发器(双) 7474 
中规模同步计数器 常用 74161 
中规模异步计数器 (2+5) 7490 
双向移位寄存器 74194